Section : Compléments
Avant : Compléments
Après : La constante de Ramanujan

Papier normalisé

Les dimensions des feuilles de papier que vous avez sous les yeux sont irrationnelles ! La norme internationale ISO 216 définit les formats utilisés dans la plupart des pays aujourd'hui, dont le très connu format A4. À l'origine, le standard fut adopté par la DIN (Deutsche Institut für Normung, organisme de normalisation et standardisation allemand) en Allemagne en 1922. Certaines grandeurs avaient été définies en France durant la Révolution, puis oubliées. La norme ISO 216 définit trois séries de format de papier, A, B et C. La série C est principalement utilisée pour les enveloppes. Voici comment est définie la série A.

Si on divise en deux une feuille, on souhaite que la plus grande et la plus petite dimension des deux moitiés restent dans le même rapport que celles de la feuille entière. Par exemple soient $ L$ et $ l$ la plus grande et la plus petite dimension d'une feuille A0. Quand on la divise en deux, on obtient deux feuilles A1 dont la plus grande dimension est $ l$ et la plus petite $ L/2$. On doit avoir :

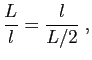
$\displaystyle \frac{L}{l} = \frac{l}{L/2}\;, $

soit $ L^2/2 = l^2$. Le rapport $ L/l$ vaut donc $ \sqrt{2}$. Les dimensions de la feuille A0 sont choisies de sorte que sa surface soit 1 mètre carré. Exprimée en mètres, $ L$ doit donc vérifier $ L^2/\sqrt{2}=1$, soit $ L=2^{1/4}$. Voici les dimensions théoriques des feuilles de papier de A0 à A4.
Papier $ L$ $ l$
A0 $ 2^{1/4}$ $ 2^{-1/4}$
A1 $ 2^{-1/4}$ $ 2^{-3/4}$
A2 $ 2^{-3/4}$ $ 2^{-5/4}$
A3 $ 2^{-5/4}$ $ 2^{-7/4}$
A4 $ 2^{-7/4}$ $ 2^{-9/4}$
Les approximations décimales à $ 10^{-3}$ près de $ 2^{-9/4}$ et $ 2^{-7/4}$ sont $ 0.210$ et $ 0.297$ ; ce sont bien les dimensions de vos feuilles de papier, exprimées en mètres.


Section : Compléments
Avant : Compléments
Après : La constante de Ramanujan


         © UJF Grenoble, 2011                              Mentions légales