Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Soit  une partie non vide et majorée de
une partie non vide et majorée de
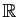 . Soit
. Soit 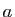 un réel.
un réel.
- Quand dit-on que
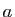 est un majorant de
est un majorant de  ?
?
- Quand dit-on que
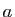 est le plus grand élément de
est le plus grand élément de  ?
?
- Quand dit-on que
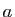 est la borne supérieure de
est la borne supérieure de  ?
?
- Quand dit-on que
 est un intervalle ?
est un intervalle ?
- Démontrer que si
 est un intervalle majoré,
non minoré, et si
est un intervalle majoré,
non minoré, et si 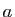 est la borne supérieure de
est la borne supérieure de  ,
alors
,
alors
![$ A=]-\infty,a [$](img349.gif) ou bien
ou bien
![$ A=]-\infty,a ]$](img350.gif) .
.
Exercice 1 :
Soit  une partie non vide de
une partie non vide de
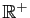 et
et 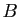 une partie non vide
de
une partie non vide
de
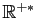 . On note
. On note 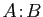 l'ensemble des quotients
d'un élément de
l'ensemble des quotients
d'un élément de  par un élément de
par un élément de 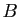 .
.
- Montrer que si
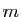 est un minorant de
est un minorant de  et
et 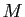 un majorant de
un majorant de 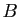 alors
alors 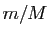 est un minorant de
est un minorant de 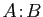 .
.
- Montrer que si
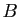 n'est pas majorée alors :
n'est pas majorée alors :
- Montrer que si
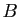 n'est pas majorée, alors
n'est pas majorée, alors
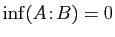 .
.
- Montrer que si
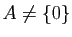 et si
et si
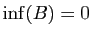 alors
alors 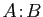 n'est pas majoré.
n'est pas majoré.
- On suppose que
 et
et 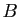 sont deux intervalles. Montrer que
sont deux intervalles. Montrer que 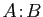 est
un intervalle.
est
un intervalle.
- Soit
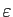 un réel strictement positif quelconque. On pose
et
un réel strictement positif quelconque. On pose
et
![$ A=B=]0,\varepsilon ]$](img358.gif) . Montrer que
. Montrer que
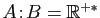 .
.
Exercice 2 :
Dans tout l'exercice,
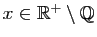 désigne un irrationnel
positif.
désigne un irrationnel
positif.
- Montrer que pour tout
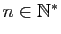 ,
,
![$ \sqrt[n]{x}=x^{1/n}$](img362.gif) est
irrationnel.
est
irrationnel.
- Montrer par un exemple que
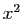 peut être rationnel.
peut être rationnel.
- Montrer que si
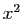 est rationnel, alors pour tout
est rationnel, alors pour tout
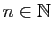 ,
,
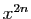 est rationnel et
est rationnel et 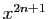 est irrationnel.
est irrationnel.
- Soient
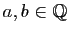 deux rationnels. Montrer que
deux rationnels. Montrer que 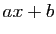 est rationnel
si et seulement si
est rationnel
si et seulement si 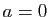 .
.
- Soient
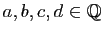 quatre rationnels. On suppose que
quatre rationnels. On suppose que 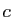 et
et
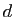 ne sont pas tous les deux nuls. Montrer que
ne sont pas tous les deux nuls. Montrer que
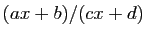 est rationnel si et seulement si
est rationnel si et seulement si 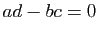 .
.
Exercice 3 :
Soient 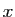 et
et 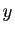 deux réels quelconques.
deux réels quelconques.
- Montrer, en utilisant l'inégalité triangulaire, que
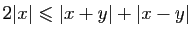 .
.
- En déduire que
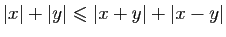 .
.
Exercice 4 :
- Soit
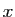 un réel et
un réel et 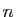 un entier. Montrer que
un entier. Montrer que
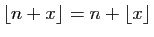 .
.
- Soient
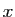 et
et 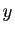 deux réels.
Montrer que
deux réels.
Montrer que
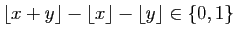 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() une partie non vide et majorée de
une partie non vide et majorée de
![]() . Soit
. Soit ![]() un réel.
un réel.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales