Montrons la seconde inclusion. Soit ![]() un réel strictement
inférieur à
un réel strictement
inférieur à ![]() . Puisque
. Puisque ![]() n'est pas minoré,
n'est pas minoré, ![]() n'est pas un
minorant. Donc il existe
n'est pas un
minorant. Donc il existe ![]() tel que
tel que ![]() .
Puisque
.
Puisque ![]() est le plus petit des majorants de
est le plus petit des majorants de
![]() ,
, ![]() n'est pas un majorant. Donc il existe
n'est pas un majorant. Donc il existe ![]() tel que
tel que
![]() . Les deux réels
. Les deux réels ![]() et
et ![]() appartiennent à
appartiennent à ![]() et sont tels
que
et sont tels
que ![]() . Comme
. Comme ![]() est un intervalle, ceci entraîne que
est un intervalle, ceci entraîne que ![]() appartient à
appartient à ![]() . Au total nous avons montré que
. Au total nous avons montré que
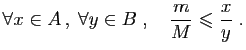
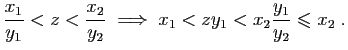
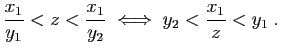
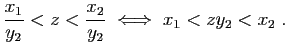
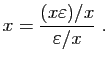
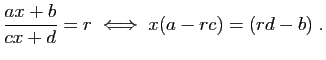
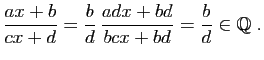
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales