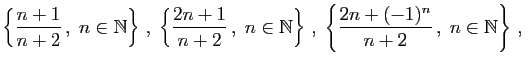
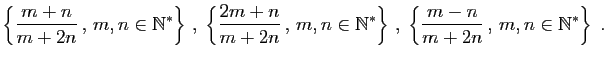
- L'ensemble est-il majoré ? minoré ?
- L'ensemble admet-il un plus grand élément ? un plus petit élément ?
- Déterminer la borne supérieure et la borne inférieure de l'ensemble.
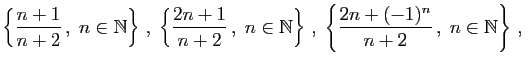
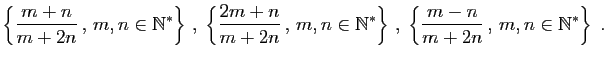
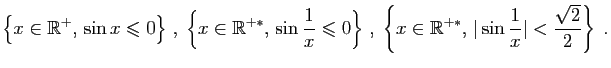
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales