-
 possède une borne supérieure, finie ou infinie.
possède une borne supérieure, finie ou infinie.
-
 Si
Si  est minorée, alors
est minorée, alors  possède une borne
inférieure finie.
possède une borne
inférieure finie.
 Si
Si
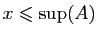 alors
alors 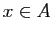 .
.
 Si
Si  contient au moins
contient au moins 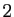 réels distincts,
alors
réels distincts,
alors  contient un rationnel.
contient un rationnel.
 Si
Si  est infinie, alors
est infinie, alors  contient une infinité d'irrationnels.
contient une infinité d'irrationnels.
-
 Si
Si  contient un intervalle de
contient un intervalle de
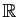 , contenant lui-même deux
points distincts, alors
, contenant lui-même deux
points distincts, alors  contient une
infinité d'irrationnels.
contient une
infinité d'irrationnels.
 Si
Si  contient un intervalle de
contient un intervalle de
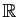 , alors
, alors  contient une
infinité de rationnels.
contient une
infinité de rationnels.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales