Dans ce cours, une relation 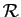 établit une correspondance
entre deux éléments d'un même
ensemble. Elle est définie par l'ensemble
établit une correspondance
entre deux éléments d'un même
ensemble. Elle est définie par l'ensemble  sur lequel elle
opère, et par son graphe
sur lequel elle
opère, et par son graphe 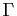 , qui est un sous-ensemble du
produit cartésien
, qui est un sous-ensemble du
produit cartésien 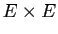 . Le fait qu'un couple
. Le fait qu'un couple 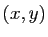 appartienne au graphe
appartienne au graphe 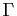 est noté
est noté
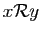 (
( est en
relation avec
est en
relation avec 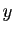 ). Considérons par exemple la relation «divise»
sur l'ensemble
). Considérons par exemple la relation «divise»
sur l'ensemble
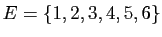 . Son graphe est :
. Son graphe est :
Ses éléments sont visualisés par des flèches sur la figure
4.
Figure:
Représentation graphique de la relation «divise» sur
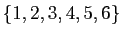 .
.
|
|
Les propriétés intéressantes que l'on attend d'une relation sont
les suivantes.
Les relations servent à traduire mathématiquement des comparaisons
entre éléments d'un même ensemble. Ces comparaisons peuvent
être de deux types.

 a le même ... que
a le même ... que 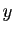 (la même valeur, la même image
par une fonction...) : c'est une relation d'équivalence.
(la même valeur, la même image
par une fonction...) : c'est une relation d'équivalence.

 est plus ... que
est plus ... que 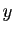 (plus petit, plus grand, plus
tôt...) : c'est une relation d'ordre.
(plus petit, plus grand, plus
tôt...) : c'est une relation d'ordre.
Définition 9
Soit 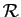 une relation sur un ensemble
une relation sur un ensemble  .
.
- On dit que
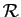 est une relation d'équivalence si
elle est à la fois réflexive, symétrique et transitive.
est une relation d'équivalence si
elle est à la fois réflexive, symétrique et transitive.
- On dit que
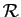 est une relation d'ordre si
elle est à la fois réflexive, anti-symétrique et transitive.
est une relation d'ordre si
elle est à la fois réflexive, anti-symétrique et transitive.
Voici des exemples de chacun des deux types de
relations.
Notre premier exemple de relation d'équivalence est la congruence
des entiers. Soit 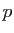 un entier strictement positif
fixé. Définissons la relation
un entier strictement positif
fixé. Définissons la relation 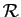 sur
sur
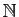 par :
par :
On dit que 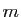 et
et  sont congrus modulo
sont congrus modulo 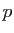 et on note
«
et on note
«
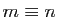 modulo
modulo 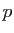 ». Il est facile de vérifier que
la congruence modulo
». Il est facile de vérifier que
la congruence modulo 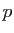 est réflexive, symétrique et
transitive. Les nombres pairs sont tous congrus à 0 modulo
est réflexive, symétrique et
transitive. Les nombres pairs sont tous congrus à 0 modulo 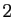 , les
nombres impairs sont congrus à
, les
nombres impairs sont congrus à 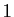 . Vérifiez sur votre agenda,
où les jours de l'année sont numérotés, que tous les lundis
sont congrus entre eux modulo 7.
. Vérifiez sur votre agenda,
où les jours de l'année sont numérotés, que tous les lundis
sont congrus entre eux modulo 7.
Pour notre deuxième exemple de relation d'équivalence, nous
allons revenir sur la notion de cardinal d'un ensemble.
Soit  un ensemble et
un ensemble et
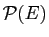 l'ensemble de ses parties.
Définissons la relation
l'ensemble de ses parties.
Définissons la relation 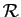 sur
sur
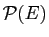 qui relie deux parties
qui relie deux parties  et
et  s'il
existe une bijection de
s'il
existe une bijection de  vers
vers  . Cette relation est :
. Cette relation est :

- réflexive : l'application identique est une
bijection de
 vers lui-même,
vers lui-même,

- symétrique : si
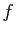 est une bijection de
est une bijection de  vers
vers
 alors l'application réciproque
alors l'application réciproque 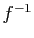 est une bijection
de
est une bijection
de  vers
vers  ,
,

- transitive : si
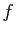 est une bijection de
est une bijection de  vers
vers  et
et 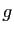 est une bijection de
est une bijection de  vers
vers 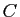 , alors
, alors 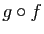 est une
bijection de
est une
bijection de  vers
vers 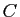 .
.
Le cardinal est la propriété commune que possèdent deux
parties reliées par cette relation d'équivalence.
Il caractérise leur classe d'équivalence.
Théorème 3
Deux classes d'équivalence sont égales ou bien disjointes.
Démonstration : Soient  et
et 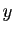 deux éléments de
deux éléments de  . Ces deux
éléments sont reliés ou ils ne le sont pas : nous distinguons
les deux cas.
. Ces deux
éléments sont reliés ou ils ne le sont pas : nous distinguons
les deux cas.
- Si
 est relié à
est relié à 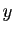 .
.
Nous allons démontrer que les deux classes sont égales.
Soit 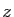 un élément de
un élément de
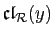 . Par définition d'une classe d'équivalence,
. Par définition d'une classe d'équivalence,
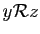 . Comme
. Comme
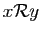 et
et
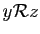 , d'après la
transitivité,
, d'après la
transitivité,
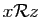 . Nous venons de montrer que tout
élément de
. Nous venons de montrer que tout
élément de
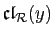 appartient aussi à
appartient aussi à
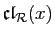 . Donc
. Donc
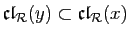 . Comme la
relation est symétrique,
. Comme la
relation est symétrique, 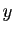 est relié à
est relié à  . Donc ce qui
précède s'applique en permutant
. Donc ce qui
précède s'applique en permutant  et
et 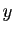 . Donc
. Donc
 . Comme les deux inclusions
sont vraies, les deux classes sont égales.
. Comme les deux inclusions
sont vraies, les deux classes sont égales.
- Si
 n'est pas relié à
n'est pas relié à 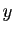 .
.
Nous allons démontrer que
l'intersection des deux classes est vide.
D'après la transitivité, pour tout 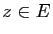 , l'implication
suivante est vraie.
, l'implication
suivante est vraie.
Donc si
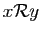 est fausse, alors l'une des deux
relations
est fausse, alors l'une des deux
relations
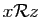 ,
,
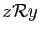 est fausse. Donc un
élément
est fausse. Donc un
élément 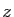 de
de  ne peut pas
appartenir à la fois à
ne peut pas
appartenir à la fois à
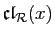 et à
et à
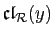 :
leur intersection est vide.
:
leur intersection est vide.

Tout élément de  appartient à sa propre classe d'équivalence
car la relation est réflexive, et à aucune autre d'après le
théorème précédent. On dit que l'ensemble des classes
d'équivalences constitue une partition de
appartient à sa propre classe d'équivalence
car la relation est réflexive, et à aucune autre d'après le
théorème précédent. On dit que l'ensemble des classes
d'équivalences constitue une partition de  (figure 5).
(figure 5).
Définition 11
Soit  un ensemble et
un ensemble et
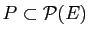 un ensemble de parties
de
un ensemble de parties
de  . On dit que
. On dit que 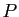 est une partition de
est une partition de  si tout
élément de
si tout
élément de  appartient à un et un seul des éléments de
appartient à un et un seul des éléments de 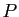 .
.
Figure 5:
Représentation graphique d'une relation
d'équivalence. Partition en classes d'équivalence.
|
|
Considérons la relation de congruence modulo 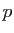 sur
sur
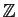 . La classe
d'équivalence de 0 est l'ensemble des multiples de
. La classe
d'équivalence de 0 est l'ensemble des multiples de 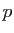 , la classe
d'équivalence de
, la classe
d'équivalence de 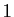 est l'ensemble de tous les entiers
est l'ensemble de tous les entiers  tels que
tels que
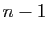 est un multiple de
est un multiple de 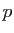 ... :
... :
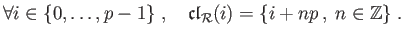
L'ensemble quotient est formé de ces 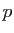 classes d'équivalence.
classes d'équivalence.
Considérons maintenant la relation d'équivalence 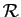 sur
sur
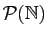 qui relie deux ensembles d'entiers
s'il existe une bijection de l'un vers l'autre. La classe
d'équivalence de
qui relie deux ensembles d'entiers
s'il existe une bijection de l'un vers l'autre. La classe
d'équivalence de
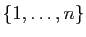 contient toutes les parties de
contient toutes les parties de
 qui
ont
qui
ont  éléments. Pour
éléments. Pour 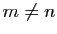 les classes de
les classes de
 et
et
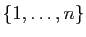 sont disjointes, car il n'existe pas de bijection
entre
sont disjointes, car il n'existe pas de bijection
entre
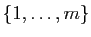 et
et
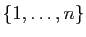 .
L'ensemble quotient de
.
L'ensemble quotient de
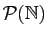 par la
relation
par la
relation 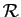 est en bijection avec
est en bijection avec
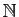 .Passons maintenant aux relations d'ordre. L'ordre le plus naturel est
celui des nombres entre eux. Observons que «
.Passons maintenant aux relations d'ordre. L'ordre le plus naturel est
celui des nombres entre eux. Observons que «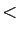 » et «
» et «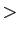 » ne sont
pas réflexives. Par contre «
» ne sont
pas réflexives. Par contre «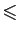 » et «
» et «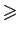 » sont bien des
relations d'ordre. Si deux éléments sont reliés par une relation
d'ordre, on dit qu'ils sont comparables. Si tous les éléments sont
comparables deux à deux, on dit que l'ordre est total. C'est
le cas pour «
» sont bien des
relations d'ordre. Si deux éléments sont reliés par une relation
d'ordre, on dit qu'ils sont comparables. Si tous les éléments sont
comparables deux à deux, on dit que l'ordre est total. C'est
le cas pour «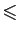 » et «
» et «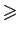 » mais pas pour la
relation «divise» sur
» mais pas pour la
relation «divise» sur
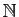 , qui est une relation d'ordre
partiel. Si
, qui est une relation d'ordre
partiel. Si  est un ensemble, l'inclusion est une relation
d'ordre partiel sur
est un ensemble, l'inclusion est une relation
d'ordre partiel sur
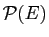 .
.
Voici un autre exemple. Supposons que  soit un alphabet, pour
lequel on a choisi un ordre total, noté
soit un alphabet, pour
lequel on a choisi un ordre total, noté 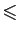 :
l'alphabet latin dont les lettres
sont rangées de «A» à «Z»,
:
l'alphabet latin dont les lettres
sont rangées de «A» à «Z», 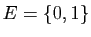 avec
avec
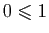 , etc... Les éléments de
, etc... Les éléments de 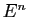 sont des
sont des  -uplets de lettres,
donc des mots de longueur
-uplets de lettres,
donc des mots de longueur  . Comment les ranger ? On peut bien sûr
définir une relation d'ordre coordonnée par coordonnée :
. Comment les ranger ? On peut bien sûr
définir une relation d'ordre coordonnée par coordonnée :
C'est bien une relation d'ordre, mais il n'est que partiel. On obtient
un ordre total en donnant la précédence à la première
coordonnée, puis à la seconde en cas d'égalité sur la
première, etc...
L'ordre est maintenant total.
Compliqué ? Pas tellement : c'est l'ordre dans lequel les mots
sont rangés dans un dictionnaire : on l'appelle
ordre lexicographique.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
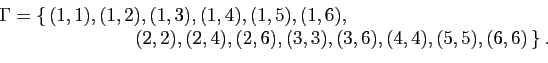
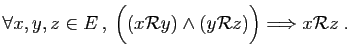
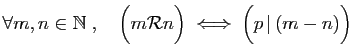
![]() un ensemble et
un ensemble et
![]() l'ensemble de ses parties.
Définissons la relation
l'ensemble de ses parties.
Définissons la relation ![]() sur
sur
![]() qui relie deux parties
qui relie deux parties ![]() et
et ![]() s'il
existe une bijection de
s'il
existe une bijection de ![]() vers
vers ![]() . Cette relation est :
. Cette relation est :
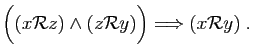
![]() appartient à sa propre classe d'équivalence
car la relation est réflexive, et à aucune autre d'après le
théorème précédent. On dit que l'ensemble des classes
d'équivalences constitue une partition de
appartient à sa propre classe d'équivalence
car la relation est réflexive, et à aucune autre d'après le
théorème précédent. On dit que l'ensemble des classes
d'équivalences constitue une partition de ![]() (figure 5).
(figure 5).
![\includegraphics[width=8cm, height=5cm]{relequiv}](img311.gif)
![]() sur
sur
![]() . La classe
d'équivalence de 0 est l'ensemble des multiples de
. La classe
d'équivalence de 0 est l'ensemble des multiples de ![]() , la classe
d'équivalence de
, la classe
d'équivalence de ![]() est l'ensemble de tous les entiers
est l'ensemble de tous les entiers ![]() tels que
tels que
![]() est un multiple de
est un multiple de ![]() ... :
... :
![]() sur
sur
![]() qui relie deux ensembles d'entiers
s'il existe une bijection de l'un vers l'autre. La classe
d'équivalence de
qui relie deux ensembles d'entiers
s'il existe une bijection de l'un vers l'autre. La classe
d'équivalence de
![]() contient toutes les parties de
contient toutes les parties de
![]() qui
ont
qui
ont ![]() éléments. Pour
éléments. Pour ![]() les classes de
les classes de
![]() et
et
![]() sont disjointes, car il n'existe pas de bijection
entre
sont disjointes, car il n'existe pas de bijection
entre
![]() et
et
![]() .
L'ensemble quotient de
.
L'ensemble quotient de
![]() par la
relation
par la
relation ![]() est en bijection avec
est en bijection avec
![]() .Passons maintenant aux relations d'ordre. L'ordre le plus naturel est
celui des nombres entre eux. Observons que «
.Passons maintenant aux relations d'ordre. L'ordre le plus naturel est
celui des nombres entre eux. Observons que «![]() » et «
» et «![]() » ne sont
pas réflexives. Par contre «
» ne sont
pas réflexives. Par contre «![]() » et «
» et «![]() » sont bien des
relations d'ordre. Si deux éléments sont reliés par une relation
d'ordre, on dit qu'ils sont comparables. Si tous les éléments sont
comparables deux à deux, on dit que l'ordre est total. C'est
le cas pour «
» sont bien des
relations d'ordre. Si deux éléments sont reliés par une relation
d'ordre, on dit qu'ils sont comparables. Si tous les éléments sont
comparables deux à deux, on dit que l'ordre est total. C'est
le cas pour «![]() » et «
» et «![]() » mais pas pour la
relation «divise» sur
» mais pas pour la
relation «divise» sur
![]() , qui est une relation d'ordre
partiel. Si
, qui est une relation d'ordre
partiel. Si ![]() est un ensemble, l'inclusion est une relation
d'ordre partiel sur
est un ensemble, l'inclusion est une relation
d'ordre partiel sur
![]() .
.
![]() soit un alphabet, pour
lequel on a choisi un ordre total, noté
soit un alphabet, pour
lequel on a choisi un ordre total, noté ![]() :
l'alphabet latin dont les lettres
sont rangées de «A» à «Z»,
:
l'alphabet latin dont les lettres
sont rangées de «A» à «Z», ![]() avec
avec
![]() , etc... Les éléments de
, etc... Les éléments de ![]() sont des
sont des ![]() -uplets de lettres,
donc des mots de longueur
-uplets de lettres,
donc des mots de longueur ![]() . Comment les ranger ? On peut bien sûr
définir une relation d'ordre coordonnée par coordonnée :
. Comment les ranger ? On peut bien sûr
définir une relation d'ordre coordonnée par coordonnée :
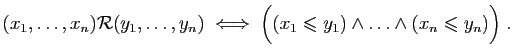
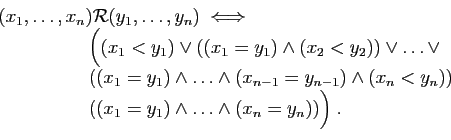
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales