Il ne s'agit pas de proposer ici une théorie du raisonnement
mathématique. Nous allons simplement donner quelques exemples de
démonstrations, pour illustrer trois types de raisonnements : par
contraposée, par l'absurde et par récurrence.
Raisonnement par contraposée
Il consiste, plutôt que de
démontrer l'implication
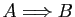 , à démontrer sa
contraposée
, à démontrer sa
contraposée
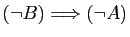 . Il est difficile de
donner une règle générale d'utilisation de ce raisonnement. Un
bon conseil avant de se lancer dans la démonstration d'une
implication, est d'écrire d'abord sa contraposée. Avec un peu
d'expérience, on arrive vite à sentir laquelle des deux est la
plus facile à démontrer.
Si le résultat désiré est
. Il est difficile de
donner une règle générale d'utilisation de ce raisonnement. Un
bon conseil avant de se lancer dans la démonstration d'une
implication, est d'écrire d'abord sa contraposée. Avec un peu
d'expérience, on arrive vite à sentir laquelle des deux est la
plus facile à démontrer.
Si le résultat désiré est  , on cherche les
conséquences de
, on cherche les
conséquences de 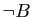 pour arriver aux bonnes hypothèses. Notre
premier exemple est un résultat facile, mais très utile.
pour arriver aux bonnes hypothèses. Notre
premier exemple est un résultat facile, mais très utile.
Proposition 9
Soit  un nombre réel tel que pour tout
un nombre réel tel que pour tout
 ,
,
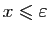 . Alors
. Alors
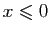 .
.
Démonstration : Nous devons démontrer l'implication :
Ecrivons sa contraposée :
«Si  est strictement positif, alors il existe
est strictement positif, alors il existe
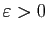 tel que
tel que
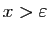 ». C'est vrai : il suffit de choisir
». C'est vrai : il suffit de choisir
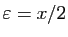 .
.
Comme deuxième exemple, nous allons reprendre un des points de la
démonstration du théorème 3.
Proposition 10
Soit 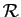 une relation d'équivalence sur un ensemble
une relation d'équivalence sur un ensemble
 . Soient
. Soient  et
et 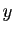 deux éléments de
deux éléments de  qui ne sont pas
reliés. Alors l'intersection des deux classes d'équivalence de
qui ne sont pas
reliés. Alors l'intersection des deux classes d'équivalence de  et
et 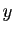 est vide.
est vide.
Démonstration : L'implication que nous devons démontrer s'écrit formellement :
Sa contraposée est :
Soit 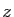 un élément de
un élément de
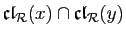 (il y
en a au moins un car l'intersection est non vide. Par définition des
classes d'équivalence,
(il y
en a au moins un car l'intersection est non vide. Par définition des
classes d'équivalence,  est relié à
est relié à  , et
, et  est relié
à
est relié
à 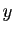 . Par transitivité,
. Par transitivité,  est relié à
est relié à 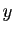 .
. Raisonnement par l'absurde
Raisonnement par l'absurde
Il consiste à démontrer une
assertion en vérifiant que sa négation conduit à une
contradiction avec les hypothèses. Dans certains cas il se distingue
mal du raisonnement par contraposée : si  désigne la
conjonction des hypothèses et
désigne la
conjonction des hypothèses et  la conclusion, nier
la conclusion, nier  et aboutir
à une contradiction, revient à démontrer
et aboutir
à une contradiction, revient à démontrer 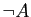 à partir de
à partir de
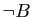 , ce qui est la contraposée de
, ce qui est la contraposée de
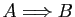 .
Notre premier exemple est dû à Euclide.
.
Notre premier exemple est dû à Euclide.
Démonstration : Supposons qu'il n'en existe qu'un nombre fini, et soit 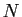 le
plus grand d'entre eux.
Considérons le nombre
le
plus grand d'entre eux.
Considérons le nombre 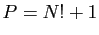 . Il est strictement
supérieur à
. Il est strictement
supérieur à 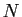 , donc il n'est pas premier, par définition de
, donc il n'est pas premier, par définition de
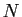 .
Si on effectue la division euclidienne de
.
Si on effectue la division euclidienne de 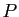 par un nombre quelconque entre 2 et
par un nombre quelconque entre 2 et 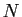 , le reste est
, le reste est 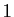 , par
définition de la factorielle (produit de tous les entiers de 1 à
, par
définition de la factorielle (produit de tous les entiers de 1 à
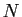 ). Donc le nombre
). Donc le nombre 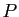 n'est divisible par aucun nombre
entre
n'est divisible par aucun nombre
entre 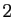 et
et 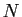 donc par aucun nombre premier : il est donc premier,
d'où la contradiction.
donc par aucun nombre premier : il est donc premier,
d'où la contradiction.
Voici un autre résultat classique.
Proposition 12
Le nombre 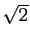 est irrationnel.
est irrationnel.
Démonstration : Un nombre rationnel est le quotient de deux entiers ; un nombre
irrationnel n'est pas rationnel. Nous devons donc démontrer que
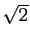 n'est pas le quotient de deux entiers. Supposons le
contraire : il existe deux entiers
n'est pas le quotient de deux entiers. Supposons le
contraire : il existe deux entiers 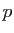 et
et 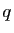 tels que
tels que
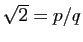 . Quitte à simplifier la fraction, nous pouvons
supposer que
. Quitte à simplifier la fraction, nous pouvons
supposer que 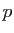 et
et 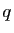 n'ont pas de facteur commun.
Multiplions par
n'ont pas de facteur commun.
Multiplions par 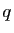 et élevons au carré :
et élevons au carré :
Le nombre 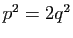 est pair, donc
est pair, donc 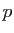 est également pair. Mais si
est également pair. Mais si
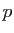 est pair, alors
est pair, alors 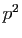 est multiple de
est multiple de 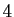 . Donc
. Donc 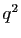 est
multiple de
est
multiple de 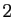 , donc
, donc 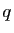 est pair. Mais alors
est pair. Mais alors 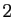 est un facteur
commun à
est un facteur
commun à 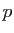 et
et 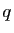 , ce qui est une contradiction.
, ce qui est une contradiction. 
Pour notre troisième exemple, nous revenons encore une fois sur :
Deux classes d'équivalence sont égales ou bien disjointes.
Comparez la démonstration qui suit avec celle du théorème
3 et de la proposition 10.
Démonstration : L'assertion  est l'hypothèse :
est l'hypothèse :
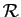 est une relation d'équivalence.
L'assertion
est une relation d'équivalence.
L'assertion  est la conclusion, que l'on peut
écrire de manière formelle comme suit.
est la conclusion, que l'on peut
écrire de manière formelle comme suit.
La négation de  s'écrit :
s'écrit :
Soit encore : il existe deux éléments  et
et 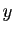 tels que les
classes
tels que les
classes
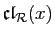 et
et
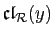 ne soient ni égales ni
disjointes. Si c'est le cas, il existe un élément
ne soient ni égales ni
disjointes. Si c'est le cas, il existe un élément 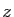 qui est dans
l'une et pas dans l'autre, et un élément
qui est dans
l'une et pas dans l'autre, et un élément 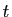 qui est dans les
deux. Supposons que
qui est dans les
deux. Supposons que 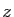 soit dans
soit dans
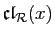 , mais pas dans
, mais pas dans
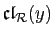 . Donc
. Donc
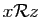 , donc
, donc
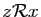 , car
, car
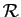 est symétrique. Mais aussi
est symétrique. Mais aussi
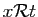 et
et
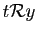 car
car
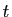 appartient aux deux classes de
appartient aux deux classes de  et
et 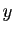 . Donc puisque
. Donc puisque 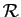 est transitive,
est transitive,
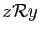 . Donc
. Donc 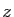 est
dans la classe de
est
dans la classe de 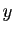 , ce qui est une contradiction.
, ce qui est une contradiction.
Raisonnement par récurrence
Pour démontrer qu'une
assertion 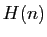 dépendant d'un entier
dépendant d'un entier  est vraie pour tout
est vraie pour tout
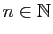 , on démontre :
, on démontre :
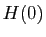 «initialisation »,
«initialisation »,
-
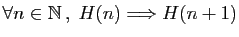 «hérédité».
«hérédité».
L'assertion 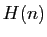 est l'hypothèse de récurrence.
Il peut se faire qu'elle ne soit vraie que pour
est l'hypothèse de récurrence.
Il peut se faire qu'elle ne soit vraie que pour
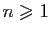 ou
ou
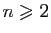 , auquel cas, on la démontre
pour la plus petite valeur pour laquelle elle est vraie.
Voici la démonstration d'une formule à connaître :
, auquel cas, on la démontre
pour la plus petite valeur pour laquelle elle est vraie.
Voici la démonstration d'une formule à connaître :
Proposition 13
Pour tout entier
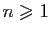 ,
la somme des entiers de 1 à
,
la somme des entiers de 1 à  vaut
vaut 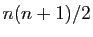 .
.
Démonstration : L'hypothèse de récurrence est :
- Initialisation.
Pour
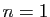 :
:
- Hérédité.
Soit
 un entier quelconque.
Supposons que
un entier quelconque.
Supposons que 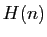 est vraie. Ecrivons :
est vraie. Ecrivons :
En appliquant 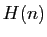 , on obtient
, on obtient
Le membre de droite s'écrit
Nous avons donc démontré que
c'est-à-dire que 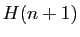 est vraie.
est vraie.

On peut être amené, pour démontrer 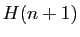 à utiliser
à utiliser
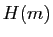 pour
pour
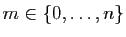 , ce qui ne change rien au principe de
la récurrence.
, ce qui ne change rien au principe de
la récurrence.
Pour deviner quelle est la bonne hypothèse 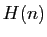 , on doit souvent
essayer plusieurs valeurs successives de
, on doit souvent
essayer plusieurs valeurs successives de  :
: 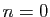 , puis
, puis
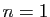 ,
, 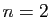 ,... C'est parfaitement inutile pour la
démonstration. Attention, ce n'est pas parce qu'une propriété
est vraie pour quelques valeurs de
,... C'est parfaitement inutile pour la
démonstration. Attention, ce n'est pas parce qu'une propriété
est vraie pour quelques valeurs de  qu'elle est vraie pour tout
qu'elle est vraie pour tout
 . Voici deux exemples.
. Voici deux exemples.
- Les nombres
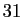 ,
, 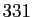 ,
, 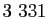 ,...,
,...,
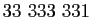 sont tous
premiers. Mais
sont tous
premiers. Mais
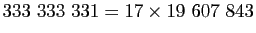 ne l'est pas.
ne l'est pas.
- Pour toutes les valeurs de
 allant de 0 à
allant de 0 à 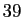 , le
nombre
, le
nombre 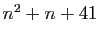 est premier. Mais le nombre
est premier. Mais le nombre
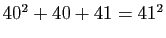 ne
l'est pas.
ne
l'est pas.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
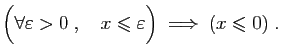
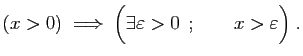
![]() dépendant d'un entier
dépendant d'un entier ![]() est vraie pour tout
est vraie pour tout
![]() , on démontre :
, on démontre :
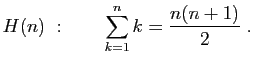
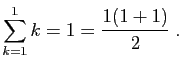
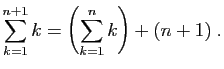
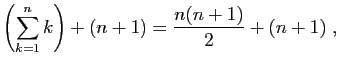
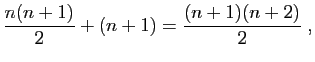
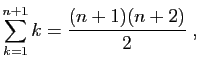
![]() à utiliser
à utiliser
![]() pour
pour
![]() , ce qui ne change rien au principe de
la récurrence.
, ce qui ne change rien au principe de
la récurrence.
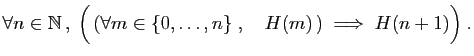
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales