Les fonctions et les applications sont des correspondances entre
ensembles. Pour définir une fonction  ,
il faut d'abord un ensemble de départ
,
il faut d'abord un ensemble de départ  (la source)
et un ensemble d'arrivée
(la source)
et un ensemble d'arrivée 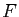 (le but). Il faut ensuite
un sous-ensemble
(le but). Il faut ensuite
un sous-ensemble 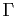 du produit cartésien de
du produit cartésien de 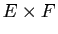 ,
c'est-à-dire un ensemble de couples
,
c'est-à-dire un ensemble de couples 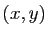 où
où 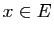 et
et 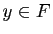 .
L'ensemble
.
L'ensemble 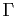 s'appelle le graphe de
la fonction. La règle de base est qu'un élément de
s'appelle le graphe de
la fonction. La règle de base est qu'un élément de  ne peut pas correspondre à deux éléments de
ne peut pas correspondre à deux éléments de 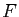 . Ceci s'écrit :
. Ceci s'écrit :
La donnée de l'ensemble de départ, de l'ensemble d'arrivée
et du graphe définit la fonction  . Si
. Si
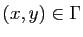 , on dit
que
, on dit
que 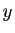 est l'image de
est l'image de 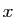 :
: 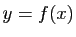 . La notation
standard pour une fonction est la suivante.
. La notation
standard pour une fonction est la suivante.
Elle se lit «fonction  de
de  vers
vers 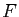 qui à
qui à 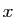 associe
associe
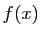 ».
».
On utilise le plus souvent fonction et application comme
des synonymes. En toute rigueur une application est une fonction telle
que tout élément de l'ensemble de départ admet une image (et une
seule). Pour une fonction, le sous-ensemble de l'ensemble de départ
formé des éléments qui ont effectivement une image s'appelle le
domaine de définition.
Dans ce chapitre, nous nous limiterons aux applications.
Attention à la notation 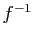 : elle ne signifie pas que
: elle ne signifie pas que
 est inversée. C'est une convention pour désigner
un sous-ensemble de l'espace de départ. Un élément
est inversée. C'est une convention pour désigner
un sous-ensemble de l'espace de départ. Un élément 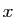 de
de  tel
que
tel
que 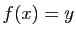 s'appelle un antécédent de
s'appelle un antécédent de 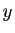 . D'après la
définition 3, l'ensemble des
antécédents de
. D'après la
définition 3, l'ensemble des
antécédents de 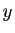 est
est
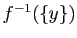 .
.
Soit
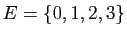 et
et
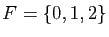 . Considérons l'application qui
à un nombre associe le reste de sa division euclidienne par 2 : 0
s'il est pair, 1 s'il est impair. Le graphe de cette application est :
. Considérons l'application qui
à un nombre associe le reste de sa division euclidienne par 2 : 0
s'il est pair, 1 s'il est impair. Le graphe de cette application est :
Il est parfois commode de représenter un graphe par un ensemble de
flèches entre deux diagrammes de Venn (figure 2).
L'image de 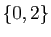 est le singleton
est le singleton  . L'image réciproque de
. L'image réciproque de
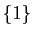 est
est 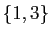 . L'image réciproque de
. L'image réciproque de 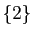 est l'ensemble vide.
est l'ensemble vide.
Figure 2:
Représentation graphique d'une application de
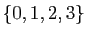 vers
vers 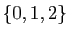 .
.
|
|
Soient  ,
, 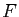 , et
, et 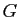 trois ensembles,
trois ensembles,  une application de
une application de  vers
vers 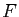 et
et 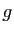 une application de
une application de 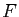 vers
vers 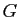 . On définit la
composée de
. On définit la
composée de  par
par 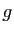 , notée
, notée 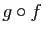 , comme
l'application de
, comme
l'application de  vers
vers 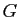 qui à
qui à 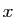 associe
associe
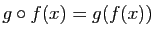 . Attention à l'ordre des applications dans
l'écriture
. Attention à l'ordre des applications dans
l'écriture 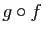 : c'est l'ordre
inverse des flèches dans le schéma ci-dessous.
: c'est l'ordre
inverse des flèches dans le schéma ci-dessous.
Définition 4
Soient  et
et 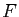 deux ensembles
et
deux ensembles
et  une application de
une application de  vers
vers
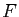 . On dit que
. On dit que  est :
est :
- injective si tout élément de l'ensemble d'arrivée
possède au plus un antécédent dans l'ensemble de départ.
- surjective si tout élément de l'ensemble d'arrivée
possède au moins un antécédent dans l'ensemble de départ.
- bijective si tout élément de l'ensemble d'arrivée
possède exactement un antécédent dans l'ensemble de départ.
Une application bijective, ou bijection, est donc à la fois
injective et surjective (voir figure 3).
Figure 3:
Représentations graphiques d'une injection, d'une
surjection et d'une bijection.
|
|
Voici comment les applications injectives, surjectives et bijectives
se comportent
vis-à-vis de la composition. La démonstration de cette assertion
est laissée au lecteur à titre d'exercice.
Proposition 3
Soient  ,
, 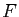 , et
, et 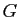 trois ensembles,
trois ensembles,
 une application de
une application de  vers
vers 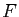 et
et 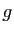 une application de
une application de 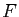 vers
vers 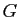 .
.
- Si
 et
et 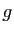 sont injectives alors
sont injectives alors 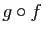 est injective.
est injective.
- Si
 et
et 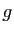 sont surjectives alors
sont surjectives alors 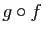 est surjective.
est surjective.
- Si
 et
et 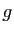 sont bijectives alors
sont bijectives alors 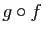 est bijective.
est bijective.
- Si
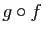 est injective alors
est injective alors  est injective.
est injective.
- Si
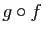 est surjective alors
est surjective alors 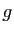 est surjective.
est surjective.
Si une application de  vers
vers 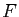 est bijective, tout
élément de
est bijective, tout
élément de 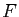 a un antécédent et un seul. On peut alors définir
l'application réciproque de
a un antécédent et un seul. On peut alors définir
l'application réciproque de  , notée
, notée 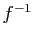 :
:
Si  est bijective, la composée de
est bijective, la composée de  par son application
réciproque
par son application
réciproque 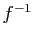 est l'application qui à
est l'application qui à 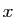 associe
associe 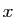 , de
, de  vers
vers  . On l'appelle application
identique, ou identité.
. On l'appelle application
identique, ou identité.
Les notations pour l'application réciproque et pour
l'image réciproque d'une partie de l'ensemble d'arrivée
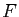 sont liées par la relation :
sont liées par la relation :
On prendra garde au fait que si l'image réciproque
d'une partie est définie pour toute application,
l'application réciproque, quant à elle, n'est définie
que pour une application bijective.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
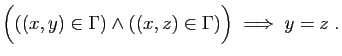
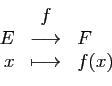
![]() et
et
![]() . Considérons l'application qui
à un nombre associe le reste de sa division euclidienne par 2 : 0
s'il est pair, 1 s'il est impair. Le graphe de cette application est :
. Considérons l'application qui
à un nombre associe le reste de sa division euclidienne par 2 : 0
s'il est pair, 1 s'il est impair. Le graphe de cette application est :
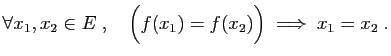
![]() est bijective, la composée de
est bijective, la composée de ![]() par son application
réciproque
par son application
réciproque ![]() est l'application qui à
est l'application qui à ![]() associe
associe ![]() , de
, de ![]() vers
vers ![]() . On l'appelle application
identique, ou identité.
. On l'appelle application
identique, ou identité.
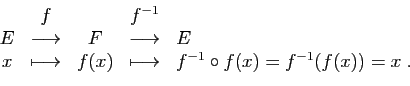
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales