L'ordre dans lequel on écrit les quantificateurs est très important. Echangeons dans (22) les deux quantificateurs.
Pour écrire la négation d'une assertion comportant des
quantificateurs on change les ![]() en
en ![]() et les
et les ![]() en
en
![]() , puis on écrit la négation de l'assertion
qui suit la liste des
quantificateurs. Ceci est tout à fait conforme à l'intuition. La
négation de «tout les
, puis on écrit la négation de l'assertion
qui suit la liste des
quantificateurs. Ceci est tout à fait conforme à l'intuition. La
négation de «tout les ![]() vérifient
vérifient ![]() » est bien «il existe un
» est bien «il existe un
![]() qui ne vérifie pas
qui ne vérifie pas ![]() ». La négation de «il existe un
». La négation de «il existe un ![]() qui vérifie
qui vérifie ![]() » est bien «aucun
» est bien «aucun ![]() ne vérifie
ne vérifie ![]() » soit
encore «tous les
» soit
encore «tous les ![]() vérifient
vérifient ![]() ».
Ecrivons par exemple la négation de l'assertion
(22).
».
Ecrivons par exemple la négation de l'assertion
(22).
Attention, les quantificateurs ne sont pas toujours distributifs par rapport à «et» et «ou». Par exemple, «il existe un entier supérieur à 7 et inférieur à 6» (faux) n'est pas équivalent à «il existe un entier supérieur à 7 et il existe un entier inférieur à 6» (vrai). De même «tout entier est inférieur ou égal à 6, ou bien supérieur ou égal à 7» (vrai) n'est pas équivalent à «tout entier est inférieur ou égal à 6 ou tout entier est supérieur ou égal à 7» (faux).
Nous commettrons souvent l'abus de notation consistant à regrouper des quantificateurs de même nature. Par exemple :
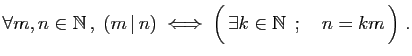
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales