Un ensemble peut être vu comme
une collection d'objets mathématiques,
appelés éléments, comme
l'ensemble
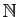 des entiers naturels. Contentez-vous pour l'instant
de l'idée intuitive d'un paquet d'éléments
possédant une propriété
commune, sur lequel on a mis une étiquette rappelant cette
propriété. Un ensemble n'est bien défini que si on peut
dire sans ambiguïté si un élément appartient ou
non à l'ensemble. Les sommets des Alpes ne
forment pas un ensemble (comment décider qu'un
endroit particulier est un sommet ?).
Par contre l'ensemble des sommets cotés sur une carte donnée
est bien défini. Deux ensembles sont égaux si et seulement si ils
contiennent les mêmes éléments.
des entiers naturels. Contentez-vous pour l'instant
de l'idée intuitive d'un paquet d'éléments
possédant une propriété
commune, sur lequel on a mis une étiquette rappelant cette
propriété. Un ensemble n'est bien défini que si on peut
dire sans ambiguïté si un élément appartient ou
non à l'ensemble. Les sommets des Alpes ne
forment pas un ensemble (comment décider qu'un
endroit particulier est un sommet ?).
Par contre l'ensemble des sommets cotés sur une carte donnée
est bien défini. Deux ensembles sont égaux si et seulement si ils
contiennent les mêmes éléments.
Le fait qu'un élément 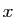 appartienne à un ensemble
appartienne à un ensemble  se note
se note 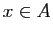 , et son contraire
, et son contraire 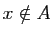 («
(«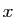 n'appartient pas
à
n'appartient pas
à  »). Par exemple
»). Par exemple
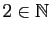 (2
appartient à
(2
appartient à
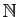 ) et
) et
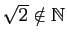 (racine de 2 n'appartient pas à
(racine de 2 n'appartient pas à
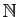 ).
Certains ensembles souvent utilisés ont une notation
propre, comme l'ensemble
).
Certains ensembles souvent utilisés ont une notation
propre, comme l'ensemble
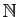 des entiers naturels, l'ensemble
des entiers naturels, l'ensemble
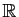 des nombres réels, l'ensemble
des nombres réels, l'ensemble
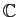 des nombres complexes. Pour les
autres, on utilise une définition, que l'on écrit entre accolades
pour dire qu'il s'agit de l'ensemble des éléments vérifiant cette
définition. On peut écrire un ensemble en extension, en donnant
la liste de ses éléments. Voici deux
définitions de l'ensemble des entiers naturels strictement
inférieurs à 5.
des nombres complexes. Pour les
autres, on utilise une définition, que l'on écrit entre accolades
pour dire qu'il s'agit de l'ensemble des éléments vérifiant cette
définition. On peut écrire un ensemble en extension, en donnant
la liste de ses éléments. Voici deux
définitions de l'ensemble des entiers naturels strictement
inférieurs à 5.
Cet énoncé se lit «ensemble des 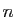 appartenant à
appartenant à
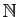 tels
que
tels
que 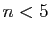 » ou «ensemble des entiers strictement
inférieurs à
» ou «ensemble des entiers strictement
inférieurs à 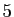 ».
Voici deux définitions de l'ensemble des diviseurs de 12.
».
Voici deux définitions de l'ensemble des diviseurs de 12.
On peut aussi définir des ensembles en extension par une liste
infinie. Le plus souvent, celle-ci se déduit de
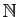 . Par exemple
l'ensemble des entiers supérieurs ou égaux à 5 :
. Par exemple
l'ensemble des entiers supérieurs ou égaux à 5 :
et l'ensemble des entiers pairs :
Les ensembles que nous définirons seront
des sous-ensembles ou parties d'un ensemble plus
grand (comme l'ensemble des entiers
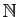 dans les exemples
précédents).
dans les exemples
précédents).
Définition 1
On dit qu'un ensemble  est un sous-ensemble ou une partie
d'un ensemble
est un sous-ensemble ou une partie
d'un ensemble  si tout élément de
si tout élément de  est aussi élément de
est aussi élément de  .
.
Si  et
et  sont deux ensembles, on note
sont deux ensembles, on note
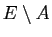 l'ensemble
formé des éléments de
l'ensemble
formé des éléments de  qui ne sont pas dans
qui ne sont pas dans  .
.
Lorsque  est un sous-ensemble de
est un sous-ensemble de  , on dit que
, on dit que
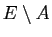 est le
complémentaire de
est le
complémentaire de  dans
dans  . On le note aussi
. On le note aussi 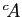 lorqu'il n'y a pas d'ambiguïté.
lorqu'il n'y a pas d'ambiguïté.
Si  est l'ensemble de référence (l'ensemble des entiers
dans nos exemples), l'ensemble des parties de
est l'ensemble de référence (l'ensemble des entiers
dans nos exemples), l'ensemble des parties de  se note
se note
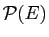 . Il contient toujours
. Il contient toujours  lui-même, ainsi que
l'ensemble vide, noté
lui-même, ainsi que
l'ensemble vide, noté
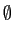 . Si
. Si  est un sous-ensemble (une partie) de
est un sous-ensemble (une partie) de  , on dit aussi
que
, on dit aussi
que  est inclus dans
est inclus dans  , et on note
, et on note
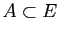 . On note
aussi
. On note
aussi
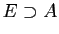 pour «
pour « contient
contient  ».
Voici l'écriture en extension de
».
Voici l'écriture en extension de
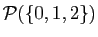 , qui est
l'ensemble des parties de l'ensemble à trois éléments
, qui est
l'ensemble des parties de l'ensemble à trois éléments
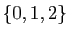 .
.
Un ensemble qui ne contient qu'un seul élément, comme  ,
est un singleton. L'ensemble
,
est un singleton. L'ensemble
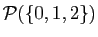 contient 8
éléments, dont chacun est lui-même un ensemble.
Il est fréquent (et souvent utile) de passer d'un ensemble
contient 8
éléments, dont chacun est lui-même un ensemble.
Il est fréquent (et souvent utile) de passer d'un ensemble  à
l'assertion
à
l'assertion 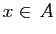 (vraie ou fausse). Les connecteurs
logiques entre assertions («non», «et», «ou»)
se traduisent par des opérations ensemblistes : complémentaire,
intersection, réunion. Nous utiliserons cette correspondance comme
définition des opérations ensemblistes.
(vraie ou fausse). Les connecteurs
logiques entre assertions («non», «et», «ou»)
se traduisent par des opérations ensemblistes : complémentaire,
intersection, réunion. Nous utiliserons cette correspondance comme
définition des opérations ensemblistes.
| ensembles |
assertions |
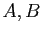 |
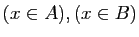 |
| complémentaire |
négation («non») |
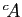 |
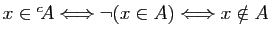 |
| intersection («inter») |
conjonction («et») |
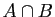 |
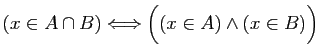 |
| réunion («union») |
disjonction («ou») |
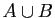 |
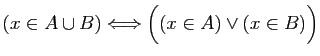 |
Au travers de ce dictionnaire l'implication
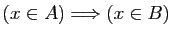
, soit
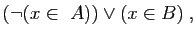
devient
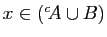 . Elle est toujours vraie si et seulement si
le complémentaire de
. Elle est toujours vraie si et seulement si
le complémentaire de
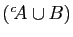 , est vide, c'est-à-dire
si
, est vide, c'est-à-dire
si  est inclus dans
est inclus dans 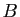 . Les propriétés
. Les propriétés 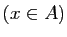 et
et
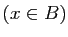 sont équivalentes si les deux inclusions
sont équivalentes si les deux inclusions
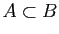 et
et
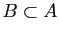 sont vraies, c'est-à-dire si les deux ensembles
contiennent les mêmes éléments. On dit qu'ils sont égaux, et
on note simplement
sont vraies, c'est-à-dire si les deux ensembles
contiennent les mêmes éléments. On dit qu'ils sont égaux, et
on note simplement 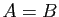 . Pour démontrer que deux ensembles sont
égaux, on doit montrer que chacun est inclus dans l'autre
(tout comme pour démontrer une équivalence, on doit
montrer les deux implications).
On déduit du théorème 1 les propriétés suivantes
des opérations ensemblistes. Les démonstrations constituent un bon
exercice de traduction, que nous laissons au lecteur. Nous
conseillons aussi de remplacer
. Pour démontrer que deux ensembles sont
égaux, on doit montrer que chacun est inclus dans l'autre
(tout comme pour démontrer une équivalence, on doit
montrer les deux implications).
On déduit du théorème 1 les propriétés suivantes
des opérations ensemblistes. Les démonstrations constituent un bon
exercice de traduction, que nous laissons au lecteur. Nous
conseillons aussi de remplacer  par
par
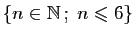 ,
, 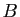 par
par
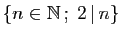 et
et 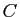 par
par
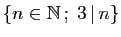 et
d'écrire en extension tous les ensembles du théorème.
et
d'écrire en extension tous les ensembles du théorème.
Théorème 2
Soient  ,
, 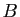 et
et 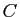 trois ensembles.
Les égalités ensemblistes suivantes sont toujours vraies.
trois ensembles.
Les égalités ensemblistes suivantes sont toujours vraies.
- Commutativité :
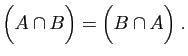 |
(13) |
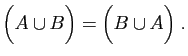 |
(14) |
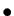
- Associativité :
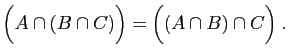 |
(15) |
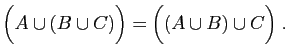 |
(16) |
- Distributivité :
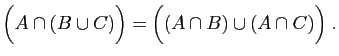 |
(17) |
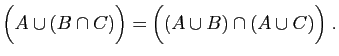 |
(18) |
- Complémentaires :
soient
 et
et 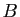 des parties d'un ensemble
des parties d'un ensemble  . Alors :
. Alors :
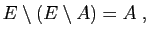 |
(19) |
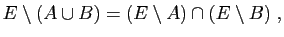 |
(20) |
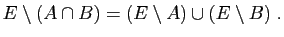 |
(21) |
Nous nous placerons toujours dans le cas où
tous les ensembles considérés sont des parties d'un
ensemble de référence  . Le complémentaire d'une partie
. Le complémentaire d'une partie  est alors
implicitement défini comme l'ensemble des éléments de
est alors
implicitement défini comme l'ensemble des éléments de  qui
n'appartiennent pas à
qui
n'appartiennent pas à  . Moyennant cette convention, le résultat
d'une opération ensembliste quelconque sur des parties de
. Moyennant cette convention, le résultat
d'une opération ensembliste quelconque sur des parties de  est
encore une partie de
est
encore une partie de  . Il est commode de visualiser
. Il est commode de visualiser  par un
rectangle et les sous-ensembles de
par un
rectangle et les sous-ensembles de  par des «patates» hachurées
dessinées dans ce rectangle. Le résultat s'appelle un
diagramme de Venn, plutôt qu'un sac de patates
(figure 1). Nous conseillons au lecteur de visualiser
les égalités ensemblistes du théorème
2 sur des diagrammes de Venn.
par des «patates» hachurées
dessinées dans ce rectangle. Le résultat s'appelle un
diagramme de Venn, plutôt qu'un sac de patates
(figure 1). Nous conseillons au lecteur de visualiser
les égalités ensemblistes du théorème
2 sur des diagrammes de Venn.
Figure 1:
Diagrammes de Venn pour le complémentaire, l'intersection et
la réunion.
|
|
Il existe d'autres manières utiles de combiner des ensembles entre
eux pour en former de nouveaux. Nous utiliserons plusieurs fois
le produit cartésien.
Le produit cartésien de  par lui-même se note
par lui-même se note 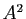 . On le
généralise à plus de deux copies de
. On le
généralise à plus de deux copies de  en définissant
en définissant 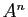 comme l'ensemble des
comme l'ensemble des 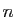 -uplets formés d'éléments de
-uplets formés d'éléments de  .
.
Attention, dans un 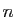 -uplet, certaines coordonnées peuvent être
identiques et l'ordre est important. Par exemple, si
-uplet, certaines coordonnées peuvent être
identiques et l'ordre est important. Par exemple, si 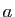 et
et 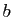 sont
deux éléments distincts
de
sont
deux éléments distincts
de  , les triplets
, les triplets 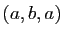 et
et 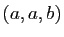 sont des
éléments distincts de
sont des
éléments distincts de 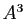 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() appartienne à un ensemble
appartienne à un ensemble ![]() se note
se note ![]() , et son contraire
, et son contraire ![]() («
(«![]() n'appartient pas
à
n'appartient pas
à ![]() »). Par exemple
»). Par exemple
![]() (2
appartient à
(2
appartient à
![]() ) et
) et
![]() (racine de 2 n'appartient pas à
(racine de 2 n'appartient pas à
![]() ).
Certains ensembles souvent utilisés ont une notation
propre, comme l'ensemble
).
Certains ensembles souvent utilisés ont une notation
propre, comme l'ensemble
![]() des entiers naturels, l'ensemble
des entiers naturels, l'ensemble
![]() des nombres réels, l'ensemble
des nombres réels, l'ensemble
![]() des nombres complexes. Pour les
autres, on utilise une définition, que l'on écrit entre accolades
pour dire qu'il s'agit de l'ensemble des éléments vérifiant cette
définition. On peut écrire un ensemble en extension, en donnant
la liste de ses éléments. Voici deux
définitions de l'ensemble des entiers naturels strictement
inférieurs à 5.
des nombres complexes. Pour les
autres, on utilise une définition, que l'on écrit entre accolades
pour dire qu'il s'agit de l'ensemble des éléments vérifiant cette
définition. On peut écrire un ensemble en extension, en donnant
la liste de ses éléments. Voici deux
définitions de l'ensemble des entiers naturels strictement
inférieurs à 5.
![]() est l'ensemble de référence (l'ensemble des entiers
dans nos exemples), l'ensemble des parties de
est l'ensemble de référence (l'ensemble des entiers
dans nos exemples), l'ensemble des parties de ![]() se note
se note
![]() . Il contient toujours
. Il contient toujours ![]() lui-même, ainsi que
l'ensemble vide, noté
lui-même, ainsi que
l'ensemble vide, noté
![]() . Si
. Si ![]() est un sous-ensemble (une partie) de
est un sous-ensemble (une partie) de ![]() , on dit aussi
que
, on dit aussi
que ![]() est inclus dans
est inclus dans ![]() , et on note
, et on note
![]() . On note
aussi
. On note
aussi
![]() pour «
pour «![]() contient
contient ![]() ».
Voici l'écriture en extension de
».
Voici l'écriture en extension de
![]() , qui est
l'ensemble des parties de l'ensemble à trois éléments
, qui est
l'ensemble des parties de l'ensemble à trois éléments
![]() .
.
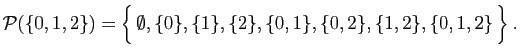
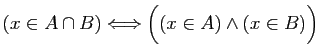
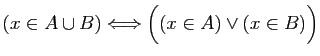
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales