On peut voir le langage mathématique comme un jeu de construction,
dont le but est de fabriquer des énoncés vrais. La règle de base
de ce jeu est qu'un énoncé mathématique ne peut être que
vrai ou faux. Il ne peut pas être «presque vrai» ou «à moitié
faux». Une des contraintes sera donc d'éviter toute
ambiguïté et chaque mot devra avoir un sens mathématique précis.
Selon le cas, un énoncé mathématique
pourra porter des noms différents.

- assertion : c'est le terme que nous utiliserons le plus
souvent pour désigner une affirmation dont on peut dire si elle est
vraie ou fausse.

- théorème : c'est un résultat important, dont on
démontre ou on admet qu'il est vrai, et qui doit être connu par
c
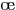 ur.
ur.

- proposition : nous utiliserons ce terme
pour désigner un
résultat démontré, moins important qu'un théorème.

- lemme : c'est un résultat démontré, qui constitue une
étape dans la démonstration d'un théorème.

- corollaire : c'est une conséquence facile d'un théorème
ou d'une proposition.
Dans ce cours les démonstrations se terminent par un carré blanc,
plutôt que par le célèbre CQFD («ce qu'il fallait démontrer»).
Pour écrire formellement des énoncés mathématiques,
on utilise des lettres représentant des concepts (nombres, ensembles,
fonctions, vecteurs, matrices, polynômes...) avec des symboles
logiques et des relations.
Le but de ce chapitre étant d'illustrer la manipulation du langage,
il ne comportera aucune difficulté mathématique. Nous en resterons
à des énoncés très simples, que l'on prendra soin de toujours
traduire en langage courant pour bien les comprendre.
Dans ce qui suit les lettres 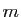 et
et  désignent des entiers naturels
(
désignent des entiers naturels
(
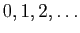 ). Nous n'utiliserons que les
symboles de comparaison (
). Nous n'utiliserons que les
symboles de comparaison (
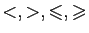 ) et de divisibilité
(
) et de divisibilité
(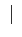 ). Rappelons que
). Rappelons que 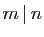 («
(«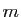 divise
divise  ») si
») si  est égal au
produit
est égal au
produit 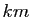 pour un certain entier
pour un certain entier 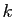 .
.
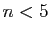 |
l'entier  est strictement inférieur à 5 est strictement inférieur à 5 |
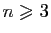 |
l'entier  est supérieur ou égal à 3 est supérieur ou égal à 3 |
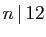 |
l'entier  divise 12 divise 12 |
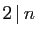 |
l'entier  est divisible par 2 (il est pair) est divisible par 2 (il est pair) |
Pour combiner entre elles des assertions, on utilise les connecteurs
de base suivants :

- la négation («non»), notée
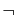

- la conjonction («et»), notée
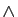

- la disjonction («ou»), notée
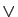 .
.
Le tableau suivant est une table de vérité. Il
décrit l'effet des connecteurs
sur deux assertions  et
et  , selon qu'elles
sont vraies (
, selon qu'elles
sont vraies (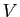 ) ou fausses (
) ou fausses (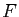 ), en disant dans chacun des 4 cas si
l'assertion composée est elle-même vraie ou fausse.
), en disant dans chacun des 4 cas si
l'assertion composée est elle-même vraie ou fausse.
Le «ou» est toujours inclusif :
 ou
ou
 signifie que l'une au moins des deux assertions est
vraie (peut-être les deux).
Par opposition, le «ou exclusif» est vrai quand l'une des deux assertions
est vraie mais pas les deux.
Voici quelques assertions composées et leur traduction.
signifie que l'une au moins des deux assertions est
vraie (peut-être les deux).
Par opposition, le «ou exclusif» est vrai quand l'une des deux assertions
est vraie mais pas les deux.
Voici quelques assertions composées et leur traduction.
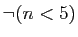 |
l'entier  n'est pas strictement inférieur à 5. n'est pas strictement inférieur à 5. |
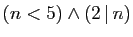 |
l'entier  est strictement inférieur à
5 et divisible par 2. est strictement inférieur à
5 et divisible par 2. |
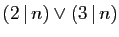 |
l'entier  est divisible par 2 ou par 3. est divisible par 2 ou par 3. |
Observez l'usage des parenthèses qui permettent d'isoler des
assertions simples au sein d'une assertion composée.
À partir des connecteurs de base, on en fabrique d'autres, dont les
plus importants sont l'implication et l'équivalence.
Par définition, l'implication
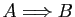 est vraie soit si
est vraie soit si  est fausse soit si
est fausse soit si  et
et  sont vraies toutes les
deux. L'écriture
sont vraies toutes les
deux. L'écriture
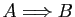 est donc une notation pour
est donc une notation pour
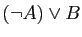 («non
(«non  ou
ou  »).
L'équivalence
»).
L'équivalence
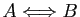 est une
double implication :
est une
double implication :
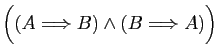 («
(« implique
implique  et
et  implique
implique  »).
Voici les tables de vérité des implications et de l'équivalence
entre deux assertions
»).
Voici les tables de vérité des implications et de l'équivalence
entre deux assertions  et
et  .
Constatez que l'équivalence
.
Constatez que l'équivalence
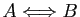 est vraie quand
est vraie quand
 et
et  sont toutes les deux vraies, ou bien toutes les deux fausses.
sont toutes les deux vraies, ou bien toutes les deux fausses.
L'implication et l'équivalence sont les
outils de base du raisonnement mathématique. Il
est essentiel de bien les assimiler, et de comprendre toutes leurs
formulations.
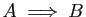 |
 implique implique  |
 entraîne entraîne  |
si  est vrai alors est vrai alors  est vrai est vrai |
 est vrai si est vrai si  est vrai est vrai |
 est vrai seulement si est vrai seulement si  est vrai est vrai |
pour que  soit vrai il suffit que soit vrai il suffit que  le soit le soit |
 est une condition suffisante pour est une condition suffisante pour  |
pour que  soit vrai il faut que soit vrai il faut que  le soit le soit |
 est une condition nécessaire pour est une condition nécessaire pour  |
Pour bien comprendre l'implication, reprenez chacune des formulations en
remplaçant  par «
par «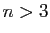 » et
» et  par «
par «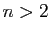 ».
».
 |
 est équivalent à est équivalent à  |
 équivaut à équivaut à  |
 entraîne entraîne  et réciproquement et réciproquement |
si  est vrai alors est vrai alors  est vrai et réciproquement est vrai et réciproquement |
 est vrai si et seulement si est vrai si et seulement si  est vrai est vrai |
pour que  soit vrai il faut et il suffit que soit vrai il faut et il suffit que  le soit le soit |
 est une condition nécessaire et suffisante pour est une condition nécessaire et suffisante pour  |
Pour bien comprendre l'équivalence, reprenez chacune des formulations en
remplaçant  par «
par «
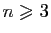 » et
» et  par «
par «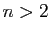 ».
».
Les principales propriétés des connecteurs sont
résumées dans le théorème suivant.
Il est conseillé de remplacer  ,
,  et
et 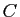 par des
assertions sur les nombres entiers pour bien comprendre les
énoncés de ce théorème (par
exemple
par des
assertions sur les nombres entiers pour bien comprendre les
énoncés de ce théorème (par
exemple  par
par
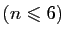 ,
,  par
par 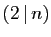 ,
, 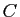 par
par 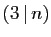 ).
Démonstration : Pour démontrer l'équivalence de deux assertions,
nous n'avons pas d'autre moyen pour
l'instant que de vérifier que leurs tables de vérité coïncident : les deux assertions sont équivalentes si elles sont
toujours soit toutes les deux vraies soit toutes les deux fausses.
Voici la vérification pour (5).
).
Démonstration : Pour démontrer l'équivalence de deux assertions,
nous n'avons pas d'autre moyen pour
l'instant que de vérifier que leurs tables de vérité coïncident : les deux assertions sont équivalentes si elles sont
toujours soit toutes les deux vraies soit toutes les deux fausses.
Voici la vérification pour (5).
L'équivalence est vraie car dans la table ci-dessous, les colonnes
correspondant aux deux assertions sont identiques.
Nous laissons au lecteur le soin de vérifier de même chacune des
autres équivalences.
Rares sont les démonstrations mathématiques qui utilisent
explicitement les tables de vérité. Une démonstration typique
est un enchaînement d'implications ou
d'équivalences, partant des hypothèses pour aboutir à la
conclusion. Ces enchaînements utilisent la
transitivité de l'implication et
de l'équivalence.
On en déduit facilement la transitivité de l'équivalence :
Démonstration : Nous utilisons (une dernière fois) les tables de vérité, pour
vérifier que quelles que soient les valeurs de vérité de  ,
,
 et
et 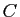 , l'implication (10) est vraie.
, l'implication (10) est vraie.
Notons

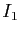 l'assertion
l'assertion
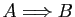 ,
,

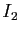 l'assertion
l'assertion
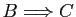 ,
,

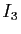 l'assertion
l'assertion
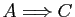 .
.

Nous utiliserons des enchaînements d'équivalences pour
démontrer le résultat suivant, qui décrit le
comportement de l'implication par
rapport à la négation.
Démonstration : Nous pourrions démontrer ces équivalences directement à l'aide
des tables de vérité (nous conseillons au lecteur de le
faire).
Nous allons plutôt les déduire du théorème
1. Voici la
démonstration de la première équivalence.
Voici la
démonstration de la seconde équivalence.

L'équivalence (11) est la méthode
habituelle que l'on utilise pour démontrer qu'une implication est
fausse : il suffit d'exhiber une situation où  est vraie et
est vraie et  fausse pour infirmer l'implication
fausse pour infirmer l'implication
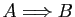 . Par exemple,
l'implication «
. Par exemple,
l'implication «
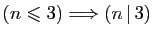 » est fausse, car
on peut trouver un entier
» est fausse, car
on peut trouver un entier  tel que
tel que
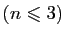 soit vrai et
soit vrai et 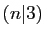 soit faux : 2 est inférieur ou égal à 3 mais ne divise pas 3.
On appelle cela «trouver un contre-exemple».
soit faux : 2 est inférieur ou égal à 3 mais ne divise pas 3.
On appelle cela «trouver un contre-exemple».
L'équivalence (12) est aussi une
technique de démonstration classique. L'implication
«
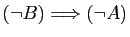 »
(«non
»
(«non  implique non
implique non  ») s'appelle la contraposée de
l'implication
») s'appelle la contraposée de
l'implication
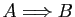 .
Par exemple, la contraposée de «
.
Par exemple, la contraposée de «
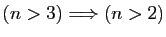 » est
«
» est
«
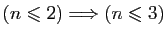 ».
Il est parfois plus facile pour
démontrer une implication de démontrer sa contraposée, nous y
reviendrons.
».
Il est parfois plus facile pour
démontrer une implication de démontrer sa contraposée, nous y
reviendrons.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales

![]() est vraie soit si
est vraie soit si ![]() est fausse soit si
est fausse soit si ![]() et
et ![]() sont vraies toutes les
deux. L'écriture
sont vraies toutes les
deux. L'écriture
![]() est donc une notation pour
est donc une notation pour
![]() («non
(«non ![]() ou
ou ![]() »).
L'équivalence
»).
L'équivalence
![]() est une
double implication :
est une
double implication :
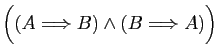 («
(«![]() implique
implique ![]() et
et ![]() implique
implique ![]() »).
Voici les tables de vérité des implications et de l'équivalence
entre deux assertions
»).
Voici les tables de vérité des implications et de l'équivalence
entre deux assertions ![]() et
et ![]() .
Constatez que l'équivalence
.
Constatez que l'équivalence
![]() est vraie quand
est vraie quand
![]() et
et ![]() sont toutes les deux vraies, ou bien toutes les deux fausses.
sont toutes les deux vraies, ou bien toutes les deux fausses.
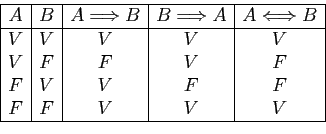

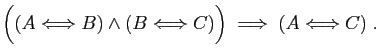

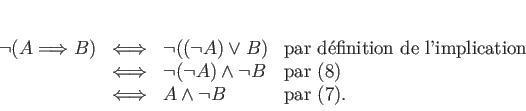
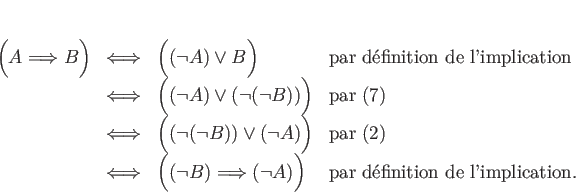
![]() est vraie et
est vraie et ![]() fausse pour infirmer l'implication
fausse pour infirmer l'implication
![]() . Par exemple,
l'implication «
. Par exemple,
l'implication «
![]() » est fausse, car
on peut trouver un entier
» est fausse, car
on peut trouver un entier ![]() tel que
tel que
![]() soit vrai et
soit vrai et ![]() soit faux : 2 est inférieur ou égal à 3 mais ne divise pas 3.
On appelle cela «trouver un contre-exemple».
soit faux : 2 est inférieur ou égal à 3 mais ne divise pas 3.
On appelle cela «trouver un contre-exemple».
![]() »
(«non
»
(«non ![]() implique non
implique non ![]() ») s'appelle la contraposée de
l'implication
») s'appelle la contraposée de
l'implication
![]() .
Par exemple, la contraposée de «
.
Par exemple, la contraposée de «
![]() » est
«
» est
«
![]() ».
Il est parfois plus facile pour
démontrer une implication de démontrer sa contraposée, nous y
reviendrons.
».
Il est parfois plus facile pour
démontrer une implication de démontrer sa contraposée, nous y
reviendrons.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales