Bertrand Russel (1872-1970) a dit «It must have required many ages
to discover that a brace of pheasants and a couple of days were both
instances of the number two». Nous
avons vu cela sous une forme moins imagée : le cardinal d'un
ensemble peut être défini comme la classe d'équivalence
des ensembles en bijection avec lui.
À la base des mathématiques, comme de toute activité
intellectuelle se trouvent les concepts. Concept en mathématiques se
dit classe d'équivalence : cela désigne une boîte fictive
dans
laquelle nous pouvons ranger toutes sortes d'objets, pourvu qu'ils
aient une propriété commune. Une fois la boîte remplie, et
dûment pourvue d'une étiquette nommant la propriété qu'elle
représente, on
peut oublier son contenu et ne plus garder que l'étiquette qui pourra
d'ailleurs devenir un nouvel objet. Cette faculté d'abstraire des
propriétés communes est essentiellement humaine. C'est l'arme qui nous
a permis de prendre une telle avance dans la lutte darwinienne pour la
survie de l'espèce. Parce que l'homme préhistorique
voyait un rapport entre un bras qui frappe et une branche qui tombe,
il a été capable d'inventer la massue. C'est aussi la base du
langage. Tout mot est une classe d'équivalence :
«bleu» ou «table» ne
sont que des boîtes pouvant contenir des objets différents. Le miracle
est que ces classes d'équivalence soient transmissibles : que deux
humains différents puissent être globalement d'accord sur les contenus de
leurs boîtes.
En mathématiques, les relations d'équivalence servent à
fabriquer toutes sortes d'ensembles. Nous n'en donnerons qu'un
exemple, la construction de l'ensemble
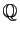 des rationnels à
partir de l'ensemble des entiers.
Un rationnel est le rapport de deux
nombres entiers, l'un entier relatif, l'autre entier naturel non nul.
des rationnels à
partir de l'ensemble des entiers.
Un rationnel est le rapport de deux
nombres entiers, l'un entier relatif, l'autre entier naturel non nul.
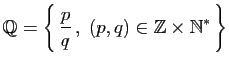
Deux couples d'entiers peuvent
représenter le même rationnel.
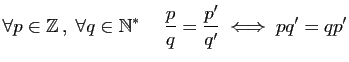
Oublions maintenant les rationnels et supposons que nous ne
connaissions que l'ensemble
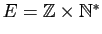 . Considérons la relation
. Considérons la relation 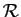 définie
sur
définie
sur  de la façon suivante.
de la façon suivante.
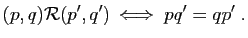
Il est facile de vérifier qu'elle est réflexive, symétrique et
transitive : c'est une relation d'équivalence. L'ensemble quotient
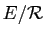 est précisément l'ensemble des rationnels. Mais pour
que cette définition soit utilisable, il faut la compléter par
les opérations dont nous avons besoin : addition, multiplication,
ordre total.
est précisément l'ensemble des rationnels. Mais pour
que cette définition soit utilisable, il faut la compléter par
les opérations dont nous avons besoin : addition, multiplication,
ordre total.
- addition : considérons l'application de
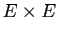 vers
vers
 qui à deux couples
qui à deux couples 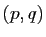 et
et 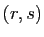 associe le couple
associe le couple
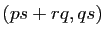 . C'est bien ce que nous attendons de l'addition des
rationnels :
. C'est bien ce que nous attendons de l'addition des
rationnels :
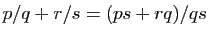 . L'application
que nous avons définie «passe au quotient» : si
. L'application
que nous avons définie «passe au quotient» : si
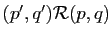 et
et
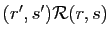 , alors
, alors
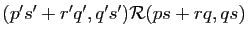 (vérifiez... !).
Si on la transporte sur l'ensemble quotient, cette
application définit l'addition des
rationnels.
(vérifiez... !).
Si on la transporte sur l'ensemble quotient, cette
application définit l'addition des
rationnels.
- multiplication : considérons
l'application de
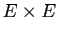 vers
vers  qui à deux couples
qui à deux couples
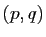 et
et 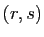 associe le couple
associe le couple
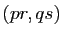 . C'est ce que nous attendons de la multiplication des
rationnels :
. C'est ce que nous attendons de la multiplication des
rationnels :
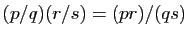 . Comme ci-dessus,
si on la transporte sur
l'ensemble quotient, l'application
définit la multiplication des rationnels.
. Comme ci-dessus,
si on la transporte sur
l'ensemble quotient, l'application
définit la multiplication des rationnels.
- ordre : considérons la relation
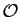 sur
sur  définie par :
définie par :
Même technique : une fois transportée sur l'ensemble quotient,
la relation 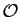 devient la relation d'ordre total que nous attendons sur
devient la relation d'ordre total que nous attendons sur
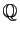 .
.
Ce que nous venons de décrire pour l'ensemble des rationnels est un
cas particulier d'une procédure très générale,
qui consiste à rajouter ce qui
manque à un ensemble en définissant une relation d'équivalence
sur un ensemble plus gros. Ainsi on peut définir
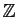 à partir de
à partir de
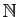 , puis
, puis
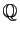 à partir de
à partir de
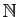 et
et
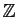 , puis
, puis
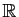 à partir
de
à partir
de
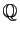 puis
puis
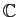 à partir de
à partir de
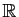 . Cela sert aussi pour des
espaces de fonctions, et encore bien d'autres objets que vous
rencontrerez plus tard.
. Cela sert aussi pour des
espaces de fonctions, et encore bien d'autres objets que vous
rencontrerez plus tard.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() des rationnels à
partir de l'ensemble des entiers.
Un rationnel est le rapport de deux
nombres entiers, l'un entier relatif, l'autre entier naturel non nul.
des rationnels à
partir de l'ensemble des entiers.
Un rationnel est le rapport de deux
nombres entiers, l'un entier relatif, l'autre entier naturel non nul.
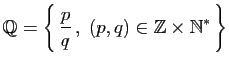
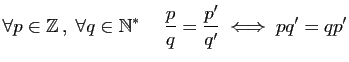
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales