Combien y a-t-il d'entiers naturels, de rationnels, de réels ? Une
infinité bien sûr. Mais l'infinité des réels est plus grande
que l'infinité des rationnels. Pour donner un sens à cette
affirmation, il faut d'abord définir ce qu'est un ensemble
dénombrable.
Définition 12
Un ensemble infini est dit dénombrable s'il existe une application
injective de cet ensemble vers
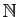 .
.
Il peut paraître paradoxal que
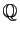 soit dénombrable. C'est
pourtant le cas, car il existe une application injective de
soit dénombrable. C'est
pourtant le cas, car il existe une application injective de
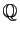 vers
vers
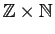 (à un rationnel
(à un rationnel 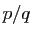 on associe le couple
on associe le couple 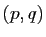 ),
et une application bijective de
),
et une application bijective de
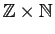 dans
dans
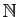 : on compte
les éléments de
: on compte
les éléments de
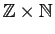 , en commençant par
, en commençant par 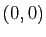 ,
puis
,
puis
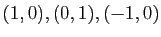 , puis
, puis
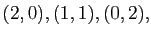
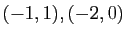 , ... Plus généralement, on démontre
que le produit et la réunion de deux ensembles dénombrables sont
eux-mêmes dénombrables.
, ... Plus généralement, on démontre
que le produit et la réunion de deux ensembles dénombrables sont
eux-mêmes dénombrables.
Théorème 4
L'ensemble des réels n'est pas dénombrable.
Démonstration : Nous allons démontrer par l'absurde que l'intervalle ![$ [0,1]$](img787.gif) n'est pas
dénombrable. Supposons que l'on puisse compter les éléments de
n'est pas
dénombrable. Supposons que l'on puisse compter les éléments de
![$ [0,1]$](img787.gif) , donc les mettre en bijection avec
, donc les mettre en bijection avec
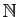 . Nous aurions
. Nous aurions
![$ [0,1]=\{ x_n ,\;n\in\mathbb{N}\}$](img788.gif) . À l'élément
. À l'élément  , nous associons un
développement décimal :
, nous associons un
développement décimal :
où les 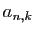 sont des entiers compris entre 0 et
sont des entiers compris entre 0 et 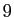 . Pour
tout
. Pour
tout 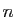 , fixons
, fixons
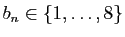 , tel que
, tel que
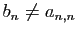 .
Considérons le réel
.
Considérons le réel 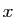 dont le développement décimal est
dont le développement décimal est
Ce réel est différent de  pour tout
pour tout 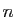 , par construction. Il
n'a donc pas pu être compté.
(Ce principe de démonstration s'appelle le procédé diagonal
de Cantor).
, par construction. Il
n'a donc pas pu être compté.
(Ce principe de démonstration s'appelle le procédé diagonal
de Cantor).
Il y a plus de réels que de rationnels, et donc plus
d'irrationnels que de rationnels. Parmi les irrationnels, on distingue
ceux qui sont solutions d'une équation polynomiale
à coefficients entiers, comme 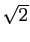 : on les appelle les
nombres algébriques. Ils semblent former une grosse
masse. Pourtant il n'y a pas plus de polynômes à coefficients
entiers que d'entiers : l'ensemble des nombres algébriques est lui
aussi dénombrable. Les nombres qui ne sont pas algébriques (on les
appelle «transcendants») forment l'essentiel des réels. Pourtant il est
extrêmement difficile de démontrer qu'un réel particulier est
transcendant. C'est une des victoires du XIXe siècle que de
l'avoir fait pour
: on les appelle les
nombres algébriques. Ils semblent former une grosse
masse. Pourtant il n'y a pas plus de polynômes à coefficients
entiers que d'entiers : l'ensemble des nombres algébriques est lui
aussi dénombrable. Les nombres qui ne sont pas algébriques (on les
appelle «transcendants») forment l'essentiel des réels. Pourtant il est
extrêmement difficile de démontrer qu'un réel particulier est
transcendant. C'est une des victoires du XIXe siècle que de
l'avoir fait pour 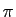 et
et
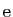 .
Existe-t-il des ensembles «intermédiaires» entre
.
Existe-t-il des ensembles «intermédiaires» entre
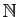 et
et
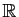 ,
qui seraient non dénombrables, sans pourtant être en bijection
avec
,
qui seraient non dénombrables, sans pourtant être en bijection
avec
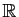 ? C'est le premier des 23 problèmes posés par Hilbert
en 1900. On a longtemps essayé d'en construire, ou de
démontrer qu'il n'en existe pas, avant de s'apercevoir finalement
que c'est une assertion indécidable : on peut la supposer vraie,
ou bien fausse, sans jamais aboutir à une contradiction. Elle
s'appelle «l'hypothèse du continu».
? C'est le premier des 23 problèmes posés par Hilbert
en 1900. On a longtemps essayé d'en construire, ou de
démontrer qu'il n'en existe pas, avant de s'apercevoir finalement
que c'est une assertion indécidable : on peut la supposer vraie,
ou bien fausse, sans jamais aboutir à une contradiction. Elle
s'appelle «l'hypothèse du continu».
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() : on les appelle les
nombres algébriques. Ils semblent former une grosse
masse. Pourtant il n'y a pas plus de polynômes à coefficients
entiers que d'entiers : l'ensemble des nombres algébriques est lui
aussi dénombrable. Les nombres qui ne sont pas algébriques (on les
appelle «transcendants») forment l'essentiel des réels. Pourtant il est
extrêmement difficile de démontrer qu'un réel particulier est
transcendant. C'est une des victoires du XIXe siècle que de
l'avoir fait pour
: on les appelle les
nombres algébriques. Ils semblent former une grosse
masse. Pourtant il n'y a pas plus de polynômes à coefficients
entiers que d'entiers : l'ensemble des nombres algébriques est lui
aussi dénombrable. Les nombres qui ne sont pas algébriques (on les
appelle «transcendants») forment l'essentiel des réels. Pourtant il est
extrêmement difficile de démontrer qu'un réel particulier est
transcendant. C'est une des victoires du XIXe siècle que de
l'avoir fait pour ![]() et
et
![]() .
Existe-t-il des ensembles «intermédiaires» entre
.
Existe-t-il des ensembles «intermédiaires» entre
![]() et
et
![]() ,
qui seraient non dénombrables, sans pourtant être en bijection
avec
,
qui seraient non dénombrables, sans pourtant être en bijection
avec
![]() ? C'est le premier des 23 problèmes posés par Hilbert
en 1900. On a longtemps essayé d'en construire, ou de
démontrer qu'il n'en existe pas, avant de s'apercevoir finalement
que c'est une assertion indécidable : on peut la supposer vraie,
ou bien fausse, sans jamais aboutir à une contradiction. Elle
s'appelle «l'hypothèse du continu».
? C'est le premier des 23 problèmes posés par Hilbert
en 1900. On a longtemps essayé d'en construire, ou de
démontrer qu'il n'en existe pas, avant de s'apercevoir finalement
que c'est une assertion indécidable : on peut la supposer vraie,
ou bien fausse, sans jamais aboutir à une contradiction. Elle
s'appelle «l'hypothèse du continu».
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales