Durant l'été 1900 un congrès international de
mathématiques se tenait à Paris. Le 8 août,
David Hilbert (1862-1943) y donne une conférence
mémorable ; selon Charles Hermite,
«on n'entendra plus jamais dans les congrès de conférences
pareilles». Qu'a-t-il donc raconté ? Un théorème exceptionnel
que lui seul pouvait démontrer ?
Une nouvelle théorie ? Pas du tout. Il s'était contenté
d'énoncer 23
problèmes, ceux qui selon lui feraient progresser la recherche en
mathématiques durant le siècle qui allait commencer. Le plus
impressionnant est que le siècle en question, qui vient de
s'achever, lui a très largement donné raison !
Dans plusieurs de ces problèmes, et en particulier dans le dixième,
Hilbert pose la question du fondement même du raisonnement
mathématique. Il souhaitait rendre explicite un système axiomatique
formel «universel». En ces temps de scientisme triomphant, personne
ne doutait que ce soit possible, et que les mathématiques finiraient
bien, après tant de victoires sur la nature, par réussir
à s'expliquer elles-mêmes.
Hilbert recherchait un système comportant des axiomes et des règles
de déduction. Un axiome est une assertion que l'on déclare vraie
a priori : par exemple 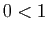 . Nous avons vu les règles de
déduction de la logique, et le moyen de déclarer vraie ou fausse
une assertion composée, en utilisant les tables de vérité.
Hilbert souhaitait un système :
. Nous avons vu les règles de
déduction de la logique, et le moyen de déclarer vraie ou fausse
une assertion composée, en utilisant les tables de vérité.
Hilbert souhaitait un système :
- consistant : aucune assertion ne peut être
à la fois vraie et fausse ;
- complet : toute assertion est soit vraie soit fausse ;
- décidable : il existe une procédure finie qui permet de
vérifier si une assertion donnée est vraie ou fausse.
On peut démontrer qu'un système consistant et complet est
forcément décidable. Une procédure de décision consiste à
ranger toutes les formules possibles d'abord par ordre de longueur,
puis par ordre lexicographique pour les formules de même
longueur. Si on doit vérifier l'assertion  , on parcourt
les formules une par une en
vérifiant pour chacune si elle est valide et si elle entraîne
, on parcourt
les formules une par une en
vérifiant pour chacune si elle est valide et si elle entraîne
 ou bien
ou bien 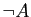 . Ce n'est pas très efficace, mais cela conduira
forcément au résultat !
En 1931 Kurt Gödel (1906-1978) ruine le rêve
de Hilbert : il démontre que dans tout système formel contenant
l'arithmétique des entiers, il existe
des propriétés telles que l'on ne
peut prouver ni qu'elles sont vraies, ni qu'elles sont fausses : on dit
qu'elles sont indécidables.
La démonstration de Gödel est trop difficile pour être
exposée ici, mais elle ressemble dans ses grandes lignes à celle
de la proposition 15. Il considère un
système consistant pour l'arithmétique des entiers.
Il construit alors une assertion
sur les nombres entiers qui exprime par elle-même
qu'elle n'est pas dénombrable : si elle est vraie, alors elle est
fausse, et si elle est fausse, alors elle est vraie. Il en déduit
que le système ne peut pas être complet.
. Ce n'est pas très efficace, mais cela conduira
forcément au résultat !
En 1931 Kurt Gödel (1906-1978) ruine le rêve
de Hilbert : il démontre que dans tout système formel contenant
l'arithmétique des entiers, il existe
des propriétés telles que l'on ne
peut prouver ni qu'elles sont vraies, ni qu'elles sont fausses : on dit
qu'elles sont indécidables.
La démonstration de Gödel est trop difficile pour être
exposée ici, mais elle ressemble dans ses grandes lignes à celle
de la proposition 15. Il considère un
système consistant pour l'arithmétique des entiers.
Il construit alors une assertion
sur les nombres entiers qui exprime par elle-même
qu'elle n'est pas dénombrable : si elle est vraie, alors elle est
fausse, et si elle est fausse, alors elle est vraie. Il en déduit
que le système ne peut pas être complet.
Parmi les exemples d'assertions indécidables,
l'axiome du choix est le plus célèbre.
Il s'agit de l'assertion affirmant que si un
ensemble  est muni d'une relation d'équivalence, alors on peut
choisir dans chacune des classes d'équivalence un élément
particulier. C'est évident si les classes d'équivalence sont finies
ou dénombrables, mais cela ne l'est pas en général. On peut
le supposer vrai, ou bien faux, sans jamais aboutir à une
contradiction.
Loin de sonner le glas de la recherche sur
les systèmes formels, le résultat négatif
de Gödel a donné une
impulsion décisive à la logique, conduisant en
particulier avec Alan Turing (1912-1954),
aux fondements de l'informatique théorique.
est muni d'une relation d'équivalence, alors on peut
choisir dans chacune des classes d'équivalence un élément
particulier. C'est évident si les classes d'équivalence sont finies
ou dénombrables, mais cela ne l'est pas en général. On peut
le supposer vrai, ou bien faux, sans jamais aboutir à une
contradiction.
Loin de sonner le glas de la recherche sur
les systèmes formels, le résultat négatif
de Gödel a donné une
impulsion décisive à la logique, conduisant en
particulier avec Alan Turing (1912-1954),
aux fondements de l'informatique théorique.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() . Nous avons vu les règles de
déduction de la logique, et le moyen de déclarer vraie ou fausse
une assertion composée, en utilisant les tables de vérité.
Hilbert souhaitait un système :
. Nous avons vu les règles de
déduction de la logique, et le moyen de déclarer vraie ou fausse
une assertion composée, en utilisant les tables de vérité.
Hilbert souhaitait un système :
![]() est muni d'une relation d'équivalence, alors on peut
choisir dans chacune des classes d'équivalence un élément
particulier. C'est évident si les classes d'équivalence sont finies
ou dénombrables, mais cela ne l'est pas en général. On peut
le supposer vrai, ou bien faux, sans jamais aboutir à une
contradiction.
Loin de sonner le glas de la recherche sur
les systèmes formels, le résultat négatif
de Gödel a donné une
impulsion décisive à la logique, conduisant en
particulier avec Alan Turing (1912-1954),
aux fondements de l'informatique théorique.
est muni d'une relation d'équivalence, alors on peut
choisir dans chacune des classes d'équivalence un élément
particulier. C'est évident si les classes d'équivalence sont finies
ou dénombrables, mais cela ne l'est pas en général. On peut
le supposer vrai, ou bien faux, sans jamais aboutir à une
contradiction.
Loin de sonner le glas de la recherche sur
les systèmes formels, le résultat négatif
de Gödel a donné une
impulsion décisive à la logique, conduisant en
particulier avec Alan Turing (1912-1954),
aux fondements de l'informatique théorique.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales