Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Les fonctions 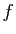 et
et 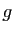 considérées ici sont supposées
définies, continues et strictement positives sur
considérées ici sont supposées
définies, continues et strictement positives sur 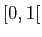 .
.
- Définir la convergence de
l'intégrale de
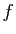 sur
sur ![$ [0,1]$](img405.gif) ·
·
- On suppose qu'il
existe
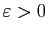 tel que pour
tout
tel que pour
tout
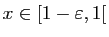 ,
,
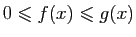 .
Démontrer que si
.
Démontrer que si
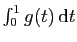 converge, alors
converge, alors
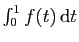 converge,
et que si
converge,
et que si
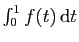 diverge, alors
diverge, alors
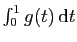 diverge.
diverge.
- On suppose maintenant que
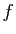 et
et 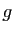 sont équivalentes au voisinage
de
sont équivalentes au voisinage
de 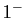 :
:
Démontrer que
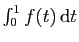 converge si et seulement si
converge si et seulement si
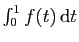 converge.
converge.
- Démontrer que pour tout réel
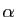 , l'intégrale
, l'intégrale
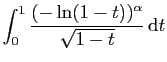 converge.
converge.
- Démontrer que l'intégrale
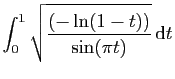 converge.
converge.
Exercice 1 :
- Démontrer que pour tout
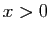 , l'intégrale
, l'intégrale
converge. On note 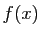 sa valeur.
sa valeur.
- En utilisant deux intégrations par parties successives, vérifier
que pour tout
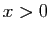 ,
,
- Démontrer que l'intégrale
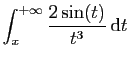 est
absolument convergente, et retrouver le résultat de la question 1.
est
absolument convergente, et retrouver le résultat de la question 1.
- Démontrer que pour tout
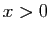 ,
,
En déduire que l'intégrale
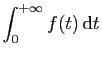 converge.
converge.
- Écrire la dérivée de
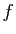 . En utilisant une intégration par
parties, montrer que
. En utilisant une intégration par
parties, montrer que
- En déduire que
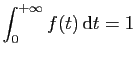 .
.
Exercice 2 :
Le but de l'exercice est de calculer
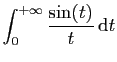 .
.
- Démontrer que l'intégrale
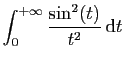 est convergente.
est convergente.
- En utilisant une intégration par parties et le changement de
variable
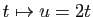 , montrer que :
, montrer que :
- Pour tout
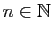 , on pose :
, on pose :
En utilisant le changement de variables
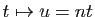 , montrer que
, montrer que
- Pour tout
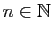 , on pose :
, on pose :
Calculer 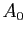 et
et 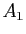 .
.
- Démontrer que pour tout
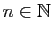 ,
,
En déduire que
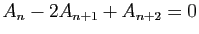 .
.
- Déduire des deux questions précédentes que pour tout
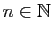 ,
,
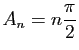 .
.
- Pour tout
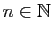 , on pose :
, on pose :
Montrer que
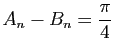 .
.
- En utilisant le fait que pour tout
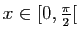 ,
,
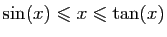 , démontrer que pour tout
, démontrer que pour tout
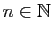 ,
,
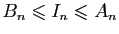 .
.
- Déduire de ce qui précède que
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() et
et ![]() considérées ici sont supposées
définies, continues et strictement positives sur
considérées ici sont supposées
définies, continues et strictement positives sur ![]() .
.
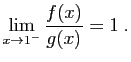
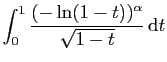 converge.
converge.
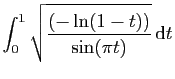 converge.
converge.
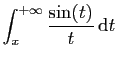
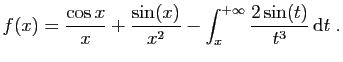
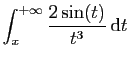 est
absolument convergente, et retrouver le résultat de la question 1.
est
absolument convergente, et retrouver le résultat de la question 1.
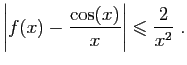
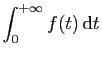 converge.
converge.
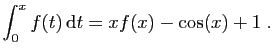
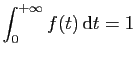 .
.
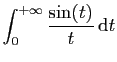 .
.
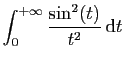 est convergente.
est convergente.
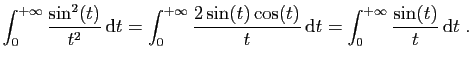
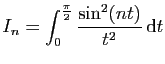
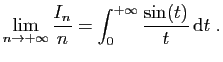
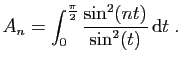
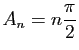 .
.
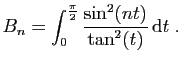
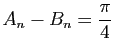 .
.
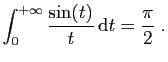
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales