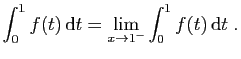
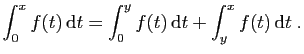
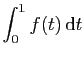 converge
converge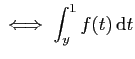 converge.
converge.
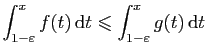
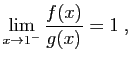
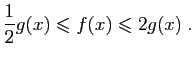
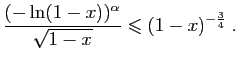
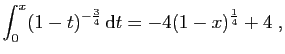
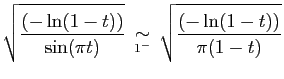
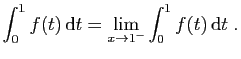
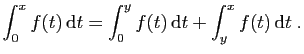
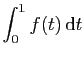 converge
converge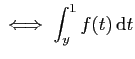 converge.
converge.
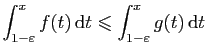
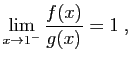
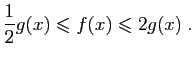
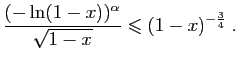
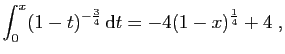
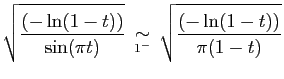
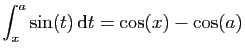
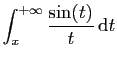 est
convergente, par application du théorème d'Abel.
est
convergente, par application du théorème d'Abel.
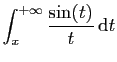 |
![$\displaystyle \displaystyle{
\left[-\frac{\cos(t)}{t}\right]_x^{+\infty} - \int_0^{+\infty}
\frac{\cos(t)}{t^2} \mathrm{d}t
}$](img510.gif) |
||
![$\displaystyle \displaystyle{
\frac{\cos(x)}{x}-\left[\frac{\sin(t)}{t^2}\right]_x^{+\infty} - \int_0^{+\infty}
\frac{2\sin(t)}{t^3} \mathrm{d}t
}$](img511.gif) |
|||
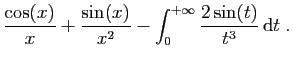 |
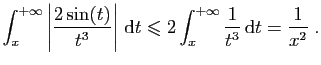
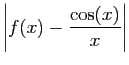 |
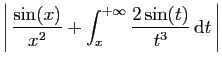 |
||
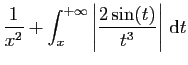 |
|||
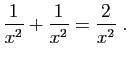 |
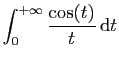 converge, en appliquant le théorème d'Abel comme dans la question
converge, en appliquant le théorème d'Abel comme dans la question
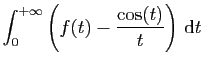 est absolument convergente. L'intégrale
est absolument convergente. L'intégrale
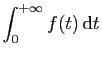 est la somme d'une
intégrale convergente et d'une intégrale absolument convergente,
donc elle converge.
est la somme d'une
intégrale convergente et d'une intégrale absolument convergente,
donc elle converge.
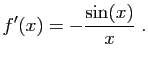
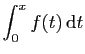 |
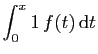 |
||
![$\displaystyle \displaystyle{\left[t f(t)\right]_0^x -\int_0^x tf'(t) \mathrm{d}t}$](img526.gif) |
|||
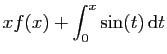 |
|||
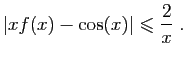
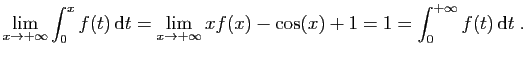
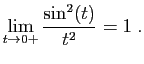
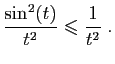
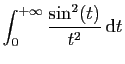 |
![$\displaystyle \displaystyle{
\left[-\frac{\sin^2(t)}{t}\right]_0^{+\infty}
+\int_0^{+\infty} \frac{2\sin(t)\cos(t)}{t} \mathrm{d}t}$](img538.gif) |
||
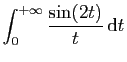 |
|||
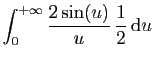 |
|||
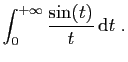 |
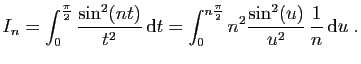
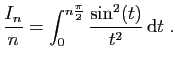
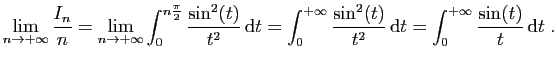
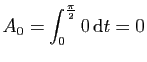 et
et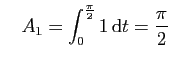
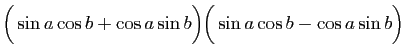 |
|||
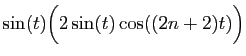 |
|||
![$\displaystyle A_n-2A_{n+1}+A_{n+2}=\int_0^{\frac{\pi}{2}} 2\cos(2(n+1)t) \mathrm{d}t
=
\left[\frac{1}{n+1}\sin(2(n+1)t)\right]_0^{\frac{\pi}{2}} = 0 \;.
$](img562.gif)
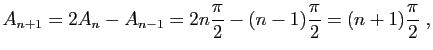
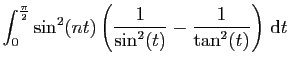 |
|||
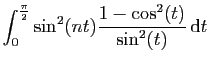 |
|||
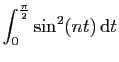 |
|||
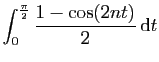 |
|||
![$\displaystyle \displaystyle{
\left[\frac{t}{2}-\frac{\sin(2nt)}{4n}\right]_0^{\frac{\pi}{2}} =
\frac{\pi}{4}\;.
}$](img570.gif) |
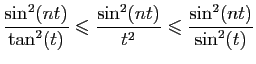
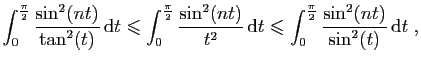
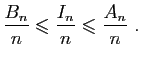
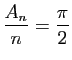 De plus d'après la question 7,
De plus d'après la question 7,
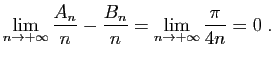
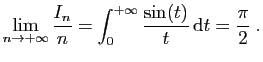
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales