-
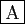
- Si l'intégrale de
 sur
sur
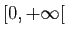 converge,
alors l'intégrale de
converge,
alors l'intégrale de  sur
sur
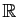 converge.
converge.
-
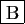
- Si l'intégrale de
 sur
sur
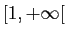 converge,
alors l'intégrale de
converge,
alors l'intégrale de  sur
sur
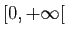 converge.
converge.
-
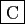
- Si
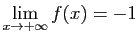 ,
alors l'intégrale de
,
alors l'intégrale de  sur
sur
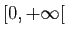 diverge.
diverge.
-
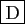
- Si l'intégrale de
 sur
sur
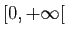 converge,
alors
converge,
alors
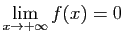 .
.
-
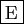
- Si
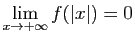 ,
alors l'intégrale de
,
alors l'intégrale de  sur
sur
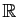 converge.
converge.
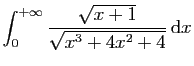
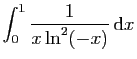
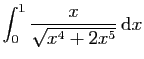
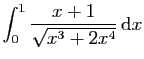
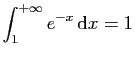
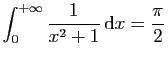
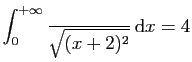
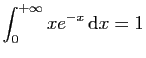
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales