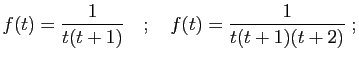
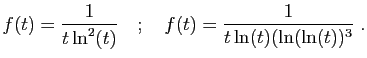
- Calculer pour tout
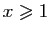 ,
,
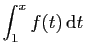 .
.
- En déduire
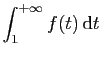 .
.
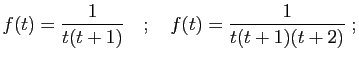
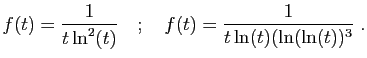
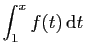 .
.
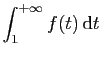 .
.
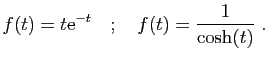
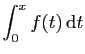 .
.
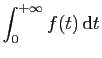 .
.
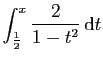 .
.
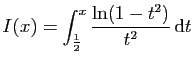 .
.
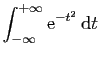 converge.
converge.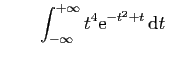 converge.
converge.
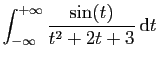 converge.
converge.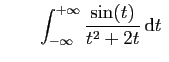 diverge.
diverge.
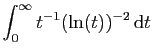 diverge.
diverge.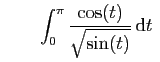 converge.
converge.
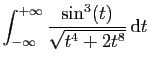 converge.
converge.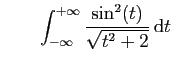 diverge.
diverge.
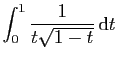 diverge.
diverge.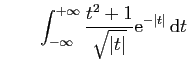 converge.
converge.
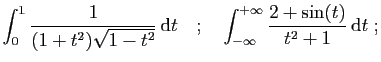
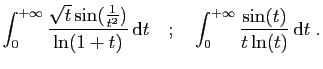
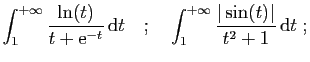
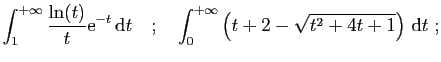
![$\displaystyle \int_0^{+\infty}\left(\sqrt[3]{t^3+1}-\sqrt{t^2+1}\right) \mathrm{d}t
\quad;\quad
\int_1^{+\infty} \mathrm{e}^{-\sqrt{t^2-t}}\mathrm{d}t
\;;
$](img352.gif)
![$\displaystyle \int_1^{+\infty}\frac{\sqrt{x}}{(\ln(t))^3} \mathrm{d}t
\quad;\q...
...nt_1^{+\infty} \frac{2+ \sin(t)+\sin^2(t)}{\sqrt[3]{t^4+t^3}} \mathrm{d}t
\;;
$](img353.gif)
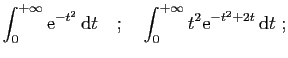
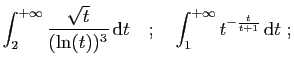
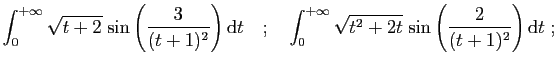
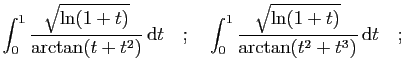
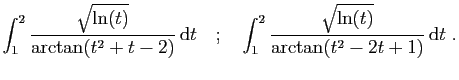
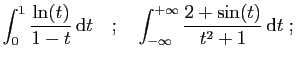
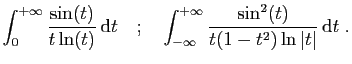
| (a) |
| (b) |
| (c) |
| (d) |
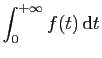 est-elle
convergente ?
est-elle
convergente ?
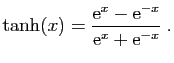
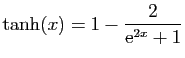 .
.
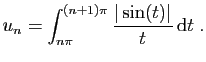
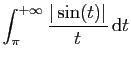 est
divergente.
est
divergente.
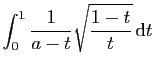 .
.
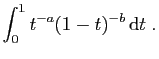
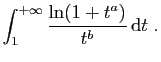
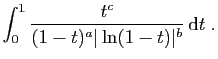
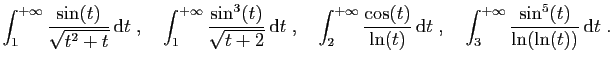
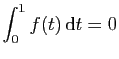 .
.
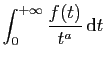 converge
pour tout
converge
pour tout 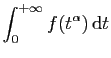 converge pour tout
converge pour tout  © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales