 Si l'intégrale de
Si l'intégrale de  sur
sur
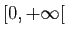 converge, alors son
intégrale sur
converge, alors son
intégrale sur
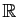 converge.
converge.
-
 Si l'intégrale de
Si l'intégrale de  sur
sur
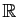 converge, alors son
intégrale sur
converge, alors son
intégrale sur
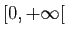 converge.
converge.
-
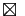 Si
Si  est une fonction paire,
alors son intégrale sur
est une fonction paire,
alors son intégrale sur
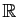 converge si et
seulement si son intégrale sur
converge si et
seulement si son intégrale sur
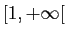 converge.
converge.
-
 Si l'intégrale de
Si l'intégrale de  sur
sur
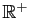 converge, alors son
intégrale sur
converge, alors son
intégrale sur
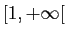 converge.
converge.
 Si
Si 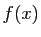 tend vers 0 quand
tend vers 0 quand 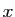 tend vers
tend vers 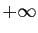 alors son
intégrale sur
alors son
intégrale sur
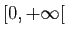 converge.
converge.
 Si l'intégrale de
Si l'intégrale de  sur
sur
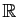 converge, alors
converge, alors 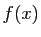 tend vers 0
quand
tend vers 0
quand 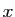 tend vers
tend vers 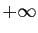 .
.
-
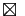 Si
Si 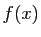 tend vers
tend vers 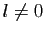 quand
quand 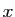 tend vers
tend vers 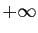 , alors son
intégrale sur
, alors son
intégrale sur
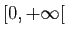 diverge.
diverge.
 Si l'intégrale de
Si l'intégrale de  sur
sur ![$ [0,x]$](img267.gif) est une fonction bornée de
est une fonction bornée de 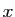 ,
alors l'intégrale de
,
alors l'intégrale de  sur
sur
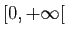 converge.
converge.
-
 Si
Si  est positive et si l'intégrale de
est positive et si l'intégrale de  sur
sur ![$ [0,x]$](img267.gif) est une fonction bornée de
est une fonction bornée de 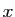 ,
alors l'intégrale de
,
alors l'intégrale de  sur
sur
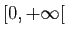 converge.
converge.
 Si pour tout
Si pour tout
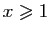 ,
,
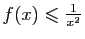 , alors l'intégrale
de
, alors l'intégrale
de  sur
sur
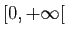 converge.
converge.
 Si
Si  est positive et si pour tout
est positive et si pour tout
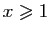 ,
,
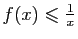 ,
alors l'intégrale de
,
alors l'intégrale de  sur
sur
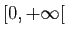 converge.
converge.
-
 Si
Si  est positive et si pour tout
est positive et si pour tout
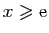 ,
,
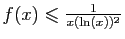 ,
alors l'intégrale de
,
alors l'intégrale de  sur
sur
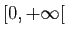 converge.
converge.
-
 Si
Si  est positive et si pour tout
est positive et si pour tout
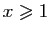 ,
,
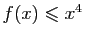 ,
alors l'intégrale de
,
alors l'intégrale de
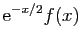 sur
sur
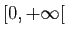 converge.
converge.
 Si pour tout
Si pour tout
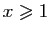 ,
,
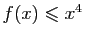 , alors l'intégrale de
, alors l'intégrale de
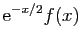 sur
sur
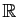 converge.
converge.
-
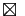 Si pour tout
Si pour tout
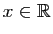 ,
,
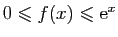 , alors l'intégrale de
, alors l'intégrale de
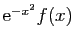 sur
sur
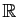 converge.
converge.
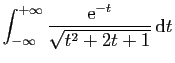
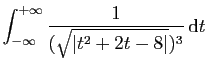
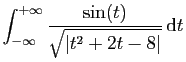
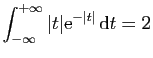
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales