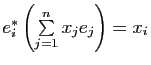 . Cette application, appelée
. Cette application, appelée
Rappels : espace vectoriel dual
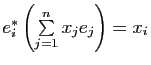 . Cette application, appelée
. Cette application, appelée
Démonstration : La première propriété découle immédiatement de la linéarité du produit scalaire.
Si ![]() et
et ![]() sont deux réels et
sont deux réels et ![]() et
et ![]() deux vecteurs de
deux vecteurs de ![]() , on a, pour tout
, on a, pour tout ![]() :
:
Comme ![]() et
et ![]() ont même dimension, il suffit, pour démontrer que c'est un isomorphisme, de vérifier qu'elle est injective, ou encore que son noyau est réduit au vecteur nul. Mais si
ont même dimension, il suffit, pour démontrer que c'est un isomorphisme, de vérifier qu'elle est injective, ou encore que son noyau est réduit au vecteur nul. Mais si ![]() est la forme linéaire nulle, on a
est la forme linéaire nulle, on a
![]() pour tout
pour tout ![]() ; en particulier, pour
; en particulier, pour ![]() , on a
, on a
![]() , d'où
, d'où ![]() .
.![]()
En particulier, pour toute base orthonormale
![]() de
de ![]() , la base duale
, la base duale
![]() est donnée par
est donnée par
![]() pour tout
pour tout
![]() , puisque
, puisque
![]() pour tout vecteur
pour tout vecteur ![]() de
de ![]() . Plus généralement, toute forme linéaire
. Plus généralement, toute forme linéaire ![]() sur
sur ![]() est de la forme
est de la forme
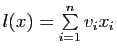 pour un
pour un ![]() -uplet
-uplet
![]() de réels, où
de réels, où
![]() sont les coordonnées du vecteur
sont les coordonnées du vecteur ![]() dans la base
dans la base
![]() , de sorte que
, de sorte que ![]() , où
, où
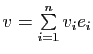 .
.
Produit vectoriel
Soit ![]() un espace vectoriel euclidien orienté de dimension
un espace vectoriel euclidien orienté de dimension ![]() ,
,
![]() une famille de
une famille de ![]() vecteurs de
vecteurs de ![]() . L'application de
. L'application de ![]() dans
dans
![]() qui à tout vecteur
qui à tout vecteur ![]() associe le produit mixte de la famille
associe le produit mixte de la famille
![]() est une forme linéaire sur
est une forme linéaire sur ![]() . Il existe donc (proposition 31) un vecteur
. Il existe donc (proposition 31) un vecteur ![]() de
de ![]() et un seul tel que
et un seul tel que
![]() pour tout vecteur
pour tout vecteur ![]() de
de ![]() . Ce vecteur est appelé produit vectoriel de la famille
. Ce vecteur est appelé produit vectoriel de la famille
![]() .
.
En particulier, pour ![]() , le produit vectoriel de deux vecteurs
, le produit vectoriel de deux vecteurs ![]() et
et ![]() d'un espace vectoriel euclidien orienté de dimension 3
est l'unique vecteur
d'un espace vectoriel euclidien orienté de dimension 3
est l'unique vecteur ![]() vérifiant
vérifiant
Propriétés
Nous nous intéresserons surtout au cas ![]() . C'est pourquoi nous donnerons les propriétés du produit vectoriel dans ce cadre.
. C'est pourquoi nous donnerons les propriétés du produit vectoriel dans ce cadre.
Démonstration : La propriété 1 provient de la linéarité du produit scalaire et des propriétés analogues du déterminant.
Si ![]() et
et ![]() sont colinéaires,
sont colinéaires, ![]() est nul par 1. Si le système
est nul par 1. Si le système ![]() est libre, on peut le compléter en une base
est libre, on peut le compléter en une base ![]() de
de ![]() et la relation
et la relation
![]() montre que
montre que ![]() n'est pas nul.
n'est pas nul.
Les relations
![]() et
et
![]() montrent que
montrent que ![]() est orthogonal à chacun des deux vecteurs
est orthogonal à chacun des deux vecteurs ![]() et
et ![]() .
.
La propriété 4 résulte de la relation
![]() si
si ![]() est un système libre.
est un système libre.
Les composantes de
![]() s'obtiennent en développant le déterminant
s'obtiennent en développant le déterminant
![]() par rapport à sa dernière colonne.
par rapport à sa dernière colonne.
La relation 6 découle de l'identité algébrique :
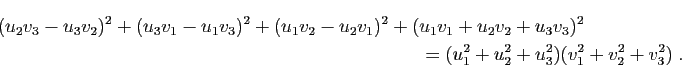
La relation 7 découle de la précédente et de la relation
![]() .
.![]()
Adjoint d'un endomorphisme
Soit ![]() un espace vectoriel euclidien et
un espace vectoriel euclidien et ![]() un endomorphisme de
un endomorphisme de ![]() (i.e. une application linéaire de
(i.e. une application linéaire de ![]() dans
dans ![]() ). Pour tout vecteur
). Pour tout vecteur ![]() de
de ![]() , l'application
, l'application
![]() de
de ![]() dans
dans
![]() est une forme linéaire sur
est une forme linéaire sur ![]() . Il existe donc un vecteur
. Il existe donc un vecteur ![]() de
de ![]() et un seul qui vérifie
et un seul qui vérifie
![]() pour tout
pour tout ![]() . On vérifie facilement que l'application
. On vérifie facilement que l'application ![]() de
de ![]() dans
dans ![]() ainsi définie est linéaire. C'est donc un endomorphisme de
ainsi définie est linéaire. C'est donc un endomorphisme de ![]() , appelé endomorphisme adjoint de
, appelé endomorphisme adjoint de ![]() .
.
Démonstration : La linéarité vient de la relation
La relation ![]() vient de même de
vient de même de
La matrice ![]() d'un endomorphisme
d'un endomorphisme ![]() dans une base orthonormée
dans une base orthonormée
![]() a pour coefficients
a pour coefficients
Un vecteur ![]() de
de ![]() appartient au noyau de
appartient au noyau de ![]() si et seulement si
si et seulement si ![]() , i.e. si et seulement si
, i.e. si et seulement si
![]() pour tout vecteur
pour tout vecteur ![]() de
de ![]() , i.e. si et seulement si
, i.e. si et seulement si ![]() est orthogonal à l'image de
est orthogonal à l'image de ![]() .
.
En remplaçant ![]() par
par ![]() dans la relation
dans la relation
![]() , on obtient
, on obtient
![]() , d'où
, d'où
![]() .
.
Le rang d'un endomorphisme est la dimension de son image. Mais :
![]()
Endomorphismes symétriques
Démonstration : L'équivalence de ![]() et
et ![]() vient de la définition de l'adjoint, l'implication
vient de la définition de l'adjoint, l'implication
![]() est évidente et les implications
est évidente et les implications
![]() et
et
![]() viennent de la proposition 33.
viennent de la proposition 33.![]()
 de l'espace des endomorphismes de
de l'espace des endomorphismes de
Démonstration : La stabilité par combinaisons linéaires de l'ensemble des endomorphismes symétriques vient de la linéarité de l'application
![]() . Soit
. Soit
![]() une base orthonormée de
une base orthonormée de ![]() . L'application qui à tout endomorphisme
. L'application qui à tout endomorphisme ![]() de
de ![]() associe sa matrice dans la base
associe sa matrice dans la base
![]() est un isomorphisme de
est un isomorphisme de
![]() sur
sur
![]() qui induit un isomorphisme du sous-espace des endomorphismes symétriques de
qui induit un isomorphisme du sous-espace des endomorphismes symétriques de ![]() sur l'espace des matrices carrées symétriques d'ordre
sur l'espace des matrices carrées symétriques d'ordre ![]() . Ce dernier est de dimension
. Ce dernier est de dimension
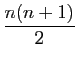 , puisqu'une matrice symétrique
, puisqu'une matrice symétrique
![]() est déterminée par les coefficients
est déterminée par les coefficients ![]() pour
pour
![]() .
.![]()
Remarque : le composé de deux endomorphismes symétriques ![]() et
et ![]() n'est en général pas symétrique ; plus précisément, il n'est symétrique que si ces endomorphismes commutent, puisque
n'est en général pas symétrique ; plus précisément, il n'est symétrique que si ces endomorphismes commutent, puisque
![]() .
.
La proposition suivante résulte immédiatement de la proposition 33 :
Exemple : projections et symétries orthogonales
Démonstration : Soit ![]() une projection sur un sous-espace vectoriel
une projection sur un sous-espace vectoriel ![]() d'un espace vectoriel euclidien
d'un espace vectoriel euclidien ![]() dans la direction d'un sous-espace
dans la direction d'un sous-espace ![]() ,
, ![]() la symétrie par rapport à
la symétrie par rapport à ![]() dans la direction
dans la direction ![]() . La relation
. La relation
![]() montre que
montre que ![]() est symétrique si et seulement si
est symétrique si et seulement si ![]() l'est. Si
l'est. Si ![]() est symétrique, son noyau
est symétrique, son noyau ![]() et son image
et son image ![]() sont supplémentaires orthogonaux d'après la proposition 36 :
sont supplémentaires orthogonaux d'après la proposition 36 : ![]() est donc une projection orthogonale. Réciproquement, si
est donc une projection orthogonale. Réciproquement, si ![]() est une projection orthogonale,
est une projection orthogonale, ![]() et
et ![]() sont supplémentaires orthogonaux et
sont supplémentaires orthogonaux et
Formes quadratiques sur un espace vectoriel euclidien
Rappels
Une forme bilinéaire symétrique sur un espace vectoriel réel ![]() est une application
est une application ![]() de
de ![]() dans
dans
![]() linéaire par rapport à chacun de ses arguments et symétrique :
linéaire par rapport à chacun de ses arguments et symétrique :
Une application ![]() de
de ![]() dans
dans
![]() est une forme quadratique sur
est une forme quadratique sur ![]() s'il existe une forme bilinéaire symétrique
s'il existe une forme bilinéaire symétrique ![]() sur
sur ![]() telle que
telle que
![]() pour tout vecteur
pour tout vecteur ![]() de
de ![]() . La forme bilinéaire symétrique
. La forme bilinéaire symétrique ![]() , appelée forme polaire de
, appelée forme polaire de ![]() , est alors uniquement déterminée, puisque
, est alors uniquement déterminée, puisque
![$\displaystyle b(x,y)=\dfrac12 [q(x+y)-q(x)-q(y)]=\dfrac14 [q(x+y)-q(x-y)] \; .$](img488.gif)
Pour tout endomorphisme symétrique ![]() de
de ![]() , l'application
, l'application ![]() :
:
![]() de
de ![]() dans
dans
![]() est une forme bilinéaire symétrique. Réciproquement :
est une forme bilinéaire symétrique. Réciproquement :
Démonstration : Pour tout vecteur ![]() de
de ![]() , l'application
, l'application
![]() de
de ![]() dans
dans
![]() est une forme linéaire sur
est une forme linéaire sur ![]() . Il en résulte (proposition 31) qu'il existe un vecteur
. Il en résulte (proposition 31) qu'il existe un vecteur ![]() et un seul tel que
et un seul tel que
![]() pour tout vecteur
pour tout vecteur ![]() de
de ![]() . Il résulte de la linéarité en
. Il résulte de la linéarité en ![]() de
de ![]() que
que ![]() est linéaire et de la symétrie de
est linéaire et de la symétrie de ![]() que
que ![]() est symétrique.
est symétrique.![]()
Réduction des matrices symétriques réelles
Démonstration : D'après la proposition 38, il existe un endomorphisme symétrique ![]() de
de ![]() tel que
tel que
![]() pour tout couple
pour tout couple ![]() de vecteurs de
de vecteurs de ![]() . Soit
. Soit
![]() une base orthonormée de
une base orthonormée de ![]() constituée de vecteurs propres de
constituée de vecteurs propres de ![]() et
et ![]() les valeurs propres correspondantes. Alors :
les valeurs propres correspondantes. Alors :
Démonstration : Soit ![]() un endomorphisme symétrique d'un espace vectoriel euclidien
un endomorphisme symétrique d'un espace vectoriel euclidien ![]() ,
, ![]() la forme quadratique associée,
la forme quadratique associée, ![]() la sphère unité de
la sphère unité de ![]() . La fonction
. La fonction ![]() est continue sur le compact
est continue sur le compact ![]() , elle est donc bornée sur
, elle est donc bornée sur ![]() et atteint son maximum
et atteint son maximum ![]() en un point
en un point ![]() de
de ![]() . On a
. On a
![]() pour tout
pour tout ![]() et donc
et donc
![]() par homogénéité pour tout
par homogénéité pour tout ![]() , d'où, pour
, d'où, pour ![]() :
:
Remarque : on vérifie immédiatement que la valeur propre ![]() introduite dans cette démonstration est la plus grande valeur propre de
introduite dans cette démonstration est la plus grande valeur propre de ![]() .
.
Démonstration : Soit
![]() . Pour tout
. Pour tout
![]() , on a:
, on a:
Démonstration du théorème 1 :
On démontre le théorème par récurrence sur la dimension ![]() de
de ![]() . Pour
. Pour ![]() , tout vecteur unitaire de
, tout vecteur unitaire de ![]() est vecteur propre de tout endomorphisme et constitue une base orthonormée de
est vecteur propre de tout endomorphisme et constitue une base orthonormée de ![]() . Supposons le théorème vrai pour tout espace vectoriel euclidien de dimension
. Supposons le théorème vrai pour tout espace vectoriel euclidien de dimension ![]() . Soit
. Soit ![]() un espace vectoriel euclidien de dimension
un espace vectoriel euclidien de dimension ![]() et
et ![]() un endomorphisme symétrique de
un endomorphisme symétrique de ![]() . D'après le lemme 2,
. D'après le lemme 2, ![]() admet une valeur propre réelle
admet une valeur propre réelle ![]() . Soit
. Soit ![]() l'espace propre associé. D'après le lemme 3, l'orthogonal
l'espace propre associé. D'après le lemme 3, l'orthogonal
![]() de
de ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() de dimension
de dimension ![]() stable par
stable par ![]() . La restriction de
. La restriction de ![]() à
à
![]() est un endomorphisme symétrique de
est un endomorphisme symétrique de
![]() . Par l'hypothèse de récurrence, il existe une base orthonormée de
. Par l'hypothèse de récurrence, il existe une base orthonormée de
![]() constituée de vecteurs propres de
constituée de vecteurs propres de ![]() . En la complétant par une base orthonormée de
. En la complétant par une base orthonormée de ![]() , on obtient une base orthonormée de
, on obtient une base orthonormée de ![]() constituée de vecteurs propres de
constituée de vecteurs propres de ![]() .
.
![]()
Démonstration : Soit ![]() une matrice réelle symétrique d'ordre
une matrice réelle symétrique d'ordre ![]() . D'après le théorème 2, il existe une matrice orthogonale
. D'après le théorème 2, il existe une matrice orthogonale ![]() et une matrice diagonale réelle
et une matrice diagonale réelle ![]() , de coefficients diagonaux les valeurs propres
, de coefficients diagonaux les valeurs propres ![]() de
de ![]() , telles que
, telles que
![]() . On a alors, pour tout vecteur colonne
. On a alors, pour tout vecteur colonne ![]() de
de
![]() :
:
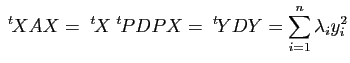
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales