-
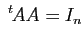 ;
;
-
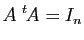 ;
;
 est inversible et
est inversible et
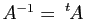 .
.
Interprétation :
La propriété 1 (resp. 2) signifie que les vecteurs colonnes (resp. lignes) de la matrice ![]() constituent un système orthonormé pour le produit scalaire canonique de
constituent un système orthonormé pour le produit scalaire canonique de
![]() . Ainsi une matrice est orthogonale si et seulement si ses vecteurs colonnes (resp. ses vecteurs lignes) constituent une base orthonormale de
. Ainsi une matrice est orthogonale si et seulement si ses vecteurs colonnes (resp. ses vecteurs lignes) constituent une base orthonormale de
![]() pour le produit scalaire canonique.
pour le produit scalaire canonique.
Autrement dit, une matrice est orthogonale si et seulement si c'est la matrice de passage de la base canonique de
![]() à une base orthonormale de
à une base orthonormale de
![]() . Plus généralement :
. Plus généralement :
Démonstration : La proposition découle immédiatement de la définition et de la relation
![]() .
.![]()
Démonstration : En utilisant la relation
![]() , on obtient
, on obtient
Attention : la réciproque est fausse : une matrice de déterminant ![]() n'est pas nécesairement orthogonale.
n'est pas nécesairement orthogonale.
Groupe orthogonal
Démonstration : Cet ensemble n'est pas vide, puisqu'il contient la matrice identité, il est stable par passage à l'inverse (proposition 10) et par produit, puisque si ![]() et
et ![]() sont orthogonales d'ordre
sont orthogonales d'ordre ![]() , alors
, alors
![]() .
.![]()
Démonstration : Cet ensemble est le noyau de l'homomorphisme de groupes de ![]() dans
dans ![]() qui à toute matrice orthogonale associe son déterminant.
qui à toute matrice orthogonale associe son déterminant.![]()
L'ensemble des matrices orthogonales d'ordre ![]() de déterminant -1 est noté
de déterminant -1 est noté ![]() . Ce n'est pas un sous-groupe de
. Ce n'est pas un sous-groupe de ![]() puisque le produit de deux matrices de
puisque le produit de deux matrices de ![]() appartient à
appartient à ![]() .
.
Orientation d'un espace vectoriel euclidien, produit mixte
Rappels : orientation d'un espace vectoriel réel
Pour tout espace vectoriel réel ![]() de dimension finie, on définit une relation binaire
de dimension finie, on définit une relation binaire
![]() sur l'ensemble des bases de
sur l'ensemble des bases de ![]() de la façon suivante : deux bases
de la façon suivante : deux bases
![]() et
et
![]() de
de ![]() sont en relation par
sont en relation par
![]() si et seulement si le déterminant de la matrice de passage de
si et seulement si le déterminant de la matrice de passage de
![]() à
à
![]() est strictement positif. On montre que cette relation est une relation d'équivalence qui divise l'ensemble des bases de
est strictement positif. On montre que cette relation est une relation d'équivalence qui divise l'ensemble des bases de ![]() en exactement deux classes. Orienter
en exactement deux classes. Orienter ![]() consiste à choisir l'une de ces classes : toutes les bases qui lui appartiennent sont dites directes, les autres indirectes. Deux bases en relation par
consiste à choisir l'une de ces classes : toutes les bases qui lui appartiennent sont dites directes, les autres indirectes. Deux bases en relation par
![]() sont dites de même sens.
sont dites de même sens.
Dans le cas d'un espace vectoriel euclidien, deux bases orthonormées sont de même sens si et seulement si la matrice de passage de l'une à l'autre est de déterminant +1.
Rappels : déterminant d'une famille de vecteurs
Le déterminant
![]() d'une famille
d'une famille
![]() de
de ![]() vecteurs relativement à une base
vecteurs relativement à une base
![]() d'un espace vectoriel
d'un espace vectoriel ![]() de dimension
de dimension ![]() est par définition le déterminant de la matrice carrée d'ordre
est par définition le déterminant de la matrice carrée d'ordre ![]() dont les colonnes sont les coordonnées de ces vecteurs dans la base
dont les colonnes sont les coordonnées de ces vecteurs dans la base
![]() . Ce déterminant dépend de la base
. Ce déterminant dépend de la base
![]() . Plus précisément, si
. Plus précisément, si
![]() et
et
![]() sont deux bases de
sont deux bases de ![]() , les déterminants d'une famille de
, les déterminants d'une famille de ![]() vecteurs de
vecteurs de ![]() relativement à ces deux bases sont reliés par la relation :
relativement à ces deux bases sont reliés par la relation :
Si ![]() est un espace vectoriel euclidien de dimension
est un espace vectoriel euclidien de dimension ![]() , le déterminant dans deux bases orthonormées de même sens d'une famille de
, le déterminant dans deux bases orthonormées de même sens d'une famille de ![]() vecteurs est le même, puisque la matrice de passage de l'une de ces bases à l'autre est orthogonale de déterminant +1. C'est ce qui permet de donner la définition suivante :
vecteurs est le même, puisque la matrice de passage de l'une de ces bases à l'autre est orthogonale de déterminant +1. C'est ce qui permet de donner la définition suivante :
Remarque :
Sans avoir à supposer l'espace vectoriel euclidien ![]() orienté, on remarque que la valeur absolue du déterminant de
orienté, on remarque que la valeur absolue du déterminant de ![]() vecteurs est la même dans toute base orthonormée de
vecteurs est la même dans toute base orthonormée de ![]() . Cette valeur absolue ne dépend pas de l'ordre dans lequel sont écrits ces vecteurs et représente, en dimension 2, l'aire du parallélogramme construit sur les 2 vecteurs, en dimension 3, le volume du parallélépipède construit sur les 3 vecteurs.
. Cette valeur absolue ne dépend pas de l'ordre dans lequel sont écrits ces vecteurs et représente, en dimension 2, l'aire du parallélogramme construit sur les 2 vecteurs, en dimension 3, le volume du parallélépipède construit sur les 3 vecteurs.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales