Deux parties ![]() et
et ![]() d'un espace vectoriel euclidien sont dites orthogonales si tout vecteur de
d'un espace vectoriel euclidien sont dites orthogonales si tout vecteur de ![]() est orthogonal à tout vecteur de
est orthogonal à tout vecteur de ![]() :
:
On appelle orthogonal d'une partie ![]() de
de ![]() , et on note
, et on note ![]() , l'ensemble des vecteurs orthogonaux à tout vecteur de
, l'ensemble des vecteurs orthogonaux à tout vecteur de ![]() :
:
Deux parties ![]() et
et ![]() d'un espace vectoriel euclidien sont dites orthogonales si tout vecteur de
d'un espace vectoriel euclidien sont dites orthogonales si tout vecteur de ![]() est orthogonal à tout vecteur de
est orthogonal à tout vecteur de ![]() :
:
On appelle orthogonal d'une partie ![]() de
de ![]() , et on note
, et on note ![]() , l'ensemble des vecteurs orthogonaux à tout vecteur de
, l'ensemble des vecteurs orthogonaux à tout vecteur de ![]() :
:
Démonstration : La propriété 1 provient de la linéarité du produit scalaire en chacune de ses variables, la propriété 2 de la définition de l'orthogonal d'une partie. L'inclusion
![]() provient, grâce à 2, de l'inclusion
provient, grâce à 2, de l'inclusion
![]() , l'inclusion
, l'inclusion
![]() de la linéarité du produit scalaire.
de la linéarité du produit scalaire.![]()
Démonstration : Soit
![]() une famille de vecteurs non nuls deux à deux orthogonaux :
une famille de vecteurs non nuls deux à deux orthogonaux :
![]() pour
pour ![]() , et soit
, et soit
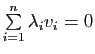 une combinaison linéaire nulle de ces vecteurs. Alors, pour tout
une combinaison linéaire nulle de ces vecteurs. Alors, pour tout
![]() :
:
Bases orthonormées
L'intérêt des bases orthonormales vient de ce que le produit scalaire et la norme ont même expression dans toute base orthonormale : si
![]() est une base orthonormale de
est une base orthonormale de ![]() et
et
 et
et
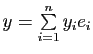 sont deux vecteurs de
sont deux vecteurs de ![]() , alors
, alors
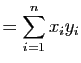 |
||
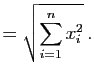 |
De plus les coordonnées d'un vecteur ![]() dans une base orthonormée
dans une base orthonormée
![]() sont données par :
sont données par :
Si on note, pour tout vecteur ![]() de
de ![]() ,
, ![]() la matrice colonne
la matrice colonne
![]() des composantes de
des composantes de ![]() dans la base orthonormée
dans la base orthonormée
![]() , le produit scalaire et la norme s'écrivent matriciellement :
, le produit scalaire et la norme s'écrivent matriciellement :
Tout espace vectoriel euclidien possède des bases orthonormées. Plus précisément le procédé d'orthonormalisation de Gram-Schmidt permet de construire à partir de n'importe quelle base d'un tel espace une base orthonormée.
Démonstration : On commence par construire une base orthogonale
![]() vérifiant
vérifiant
![]() pour tout
pour tout
![]() . Il suffit ensuite de normer cette base en posant
. Il suffit ensuite de normer cette base en posant
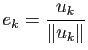 pour tout
pour tout ![]() .
.
On construit donc, par récurrence sur ![]() , une famille
, une famille
![]() de vecteurs deux à deux orthogonaux vérifiant
de vecteurs deux à deux orthogonaux vérifiant
![]() pour tout
pour tout
![]() . Pour
. Pour ![]() , il suffit de poser
, il suffit de poser ![]() . Si la famille
. Si la famille
![]() est construite pour un entier
est construite pour un entier ![]() , on cherche
, on cherche ![]() de la forme
de la forme
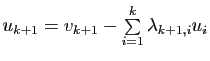 . En écrivant
. En écrivant
![]() , on obtient
, on obtient
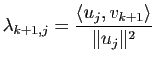 pour
pour
![]() et on vérifie immédiatement que la famille ainsi construite convient.
et on vérifie immédiatement que la famille ainsi construite convient.![]()
La matrice de passage de la base
![]() à la base
à la base
![]() est donc triangulaire supérieure. On peut montrer que la base orthonormée
est donc triangulaire supérieure. On peut montrer que la base orthonormée
![]() vérifiant ces propriétés est unique si on impose de plus à tous les coefficients diagonaux de cette matrice de passage d'être positifs.
vérifiant ces propriétés est unique si on impose de plus à tous les coefficients diagonaux de cette matrice de passage d'être positifs.
Démonstration : Soit
![]() une famille orthonormée. D'après la proposition 4, cette famille est libre. D'après le théorème de la base incomplète, on peut donc la compléter en une base
une famille orthonormée. D'après la proposition 4, cette famille est libre. D'après le théorème de la base incomplète, on peut donc la compléter en une base
![]() de
de ![]() . En orthonormalisant cette base par le procédé de Gram-Schmidt, on obtient une base orthonormée
. En orthonormalisant cette base par le procédé de Gram-Schmidt, on obtient une base orthonormée
![]() dont les
dont les ![]() premiers vecteurs coïncident avec ceux de la famille donnée.
premiers vecteurs coïncident avec ceux de la famille donnée.![]()
Démonstration : Soit
![]() une base orthonormée de
une base orthonormée de ![]() . On peut la compléter en une base orthonormée
. On peut la compléter en une base orthonormée
![]() de
de ![]() . Un vecteur
. Un vecteur
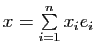 est orthogonal à
est orthogonal à ![]() si et seulement si il est orthogonal à
si et seulement si il est orthogonal à
![]() puisque ces vecteurs engendrent
puisque ces vecteurs engendrent ![]() , donc si et seulement si
, donc si et seulement si ![]() pour tout
pour tout
![]() . Le sous-espace vectoriel
. Le sous-espace vectoriel ![]() est donc le sous-espace vectoriel de
est donc le sous-espace vectoriel de ![]() engendré par
engendré par
![]() .
. ![]()
Plus généralement, pour toute partie ![]() de
de ![]() , le biorthogonal
, le biorthogonal
![]() de
de ![]() est le sous-espace vectoriel
est le sous-espace vectoriel ![]() de
de ![]() engendré par
engendré par ![]() .
.
Démonstration : L'inclusion
![]() est claire, puisque, pour tout
est claire, puisque, pour tout ![]() et tout
et tout
![]() , on a
, on a
![]() . Mais
. Mais
Si ![]() est une partie quelconque de
est une partie quelconque de ![]() , l'orthogonal de
, l'orthogonal de ![]() est aussi l'orthogonal de
est aussi l'orthogonal de ![]() , d'où
, d'où
Exemple : orthogonal d'un vecteur, vecteur normal à un hyperplan
Le sous-espace vectoriel de ![]() orthogonal à un vecteur
orthogonal à un vecteur ![]() non nul est un sous-espace vectoriel de
non nul est un sous-espace vectoriel de ![]() de dimension
de dimension ![]() , i.e. un hyperplan de
, i.e. un hyperplan de ![]() . C'est aussi le sous-espace vectoriel de
. C'est aussi le sous-espace vectoriel de ![]() orthogonal à la droite vectorielle engendrée par ce vecteur.
orthogonal à la droite vectorielle engendrée par ce vecteur.
De même, le sous-espace vectoriel orthogonal à un hyperplan ![]() de
de ![]() est une droite vectorielle de
est une droite vectorielle de ![]() . Tout vecteur non nul de cette droite est dit normal à
. Tout vecteur non nul de cette droite est dit normal à ![]() .
.
Équation d'un hyperplan :
Soit ![]() un espace vectoriel euclidien,
un espace vectoriel euclidien,
![]() une base orthonormée de
une base orthonormée de ![]() ,
, ![]() un hyperplan de
un hyperplan de ![]() et
et
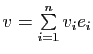 un vecteur normal à
un vecteur normal à ![]() . Alors l'équation de
. Alors l'équation de ![]() dans la base
dans la base
![]() s'écrit :
s'écrit :
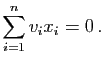
Projection et symétrie orthogonales
Rappel : si ![]() et
et ![]() sont deux sous-espaces vectoriels supplémentaires d'un espace vectoriel
sont deux sous-espaces vectoriels supplémentaires d'un espace vectoriel ![]() , tout vecteur
, tout vecteur ![]() de
de ![]() s'écrit de manière unique sous la forme
s'écrit de manière unique sous la forme ![]() , avec
, avec ![]() et
et ![]() . L'application
. L'application ![]() qui à
qui à ![]() associe
associe ![]() est une application linéaire de
est une application linéaire de ![]() dans
dans ![]() , appelée projection sur
, appelée projection sur ![]() dans la direction
dans la direction ![]() . Elle vérifie
. Elle vérifie
![]() , son image est
, son image est ![]() et son noyau
et son noyau ![]() . L'application
. L'application ![]() qui à
qui à ![]() associe
associe ![]() est une application linéaire involutive (
est une application linéaire involutive (
![]() ), donc bijective, de
), donc bijective, de ![]() sur
sur ![]() , appelée symétrie par rapport à
, appelée symétrie par rapport à ![]() dans la direction
dans la direction ![]() . Ces deux applications linéaires sont reliées par la relation
. Ces deux applications linéaires sont reliées par la relation
![]() .
.
Le projeté orthogonal ![]() sur
sur ![]() d'un vecteur
d'un vecteur ![]() de
de ![]() est donc caractérisé par les deux relations
est donc caractérisé par les deux relations ![]() et
et
![]() pour tout
pour tout ![]() .
.
Démonstration : Soit ![]() la projection orthogonale sur un sous-espace vectoriel
la projection orthogonale sur un sous-espace vectoriel ![]() d'un espace vectoriel euclidien
d'un espace vectoriel euclidien ![]() .
L'orthogonalité des vecteurs
.
L'orthogonalité des vecteurs ![]() et
et ![]() implique
implique
![]() , d'où
, d'où
![]() .
.![]()
Une réflexion est donc, dans le plan, une symétrie orthogonale par rapport à une droite et, dans l'espace, une symétrie orthogonale par rapport à un plan.
Exemple : cas d'une droite, d'un hyperplan
Soit ![]() un vecteur non nul de
un vecteur non nul de ![]() ,
,
![]() la droite vectorielle engendrée par
la droite vectorielle engendrée par ![]() et
et ![]() l'hyperplan de
l'hyperplan de ![]() orthogonal à
orthogonal à ![]() , i.e. le supplémentaire orthogonal de
, i.e. le supplémentaire orthogonal de ![]() . Le projeté orthogonal
. Le projeté orthogonal ![]() d'un vecteur
d'un vecteur ![]() de
de ![]() sur
sur ![]() est de la forme
est de la forme ![]() pour un réel
pour un réel ![]() . En écrivant que
. En écrivant que
![]() , on obtient
, on obtient
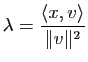 , d'où :
, d'où :
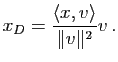
Le projeté orthogonal de ![]() sur
sur ![]() est donc :
est donc :
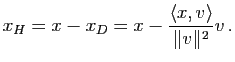
L'image de ![]() par la réflexion
par la réflexion ![]() d'hyperplan
d'hyperplan ![]() est donc
est donc
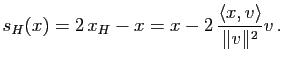
Si ![]() (resp.
(resp. ![]() ,
, ![]() ) est la matrice colonne des composantes de
) est la matrice colonne des composantes de ![]() (resp.
(resp. ![]() ,
, ![]() ) dans une base orthonormée
) dans une base orthonormée
![]() , cette relation s'écrit
, cette relation s'écrit
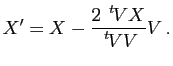
La matrice dans la base
![]() de la réflexion
de la réflexion ![]() est donc
est donc
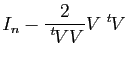 , où
, où ![]() est la matrice identité d'ordre
est la matrice identité d'ordre ![]() .
.
Ces matrices jouent un rôle important en analyse numérique, où elles sont appelées matrices de Householder.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales