Définitions

Définition 1 Un produit scalaire sur un espace vectoriel réel est une forme bilinéaire symétrique définie positive sur .

On notera dans cette section $\langle u,v\rangle$ le produit scalaire de deux vecteurs et . Dans la section «Géométrie affine euclidienne», dont le cadre sera un espace affine euclidien (souvent de dimension 2 ou 3), les vecteurs seront écrits avec des flèches pour les distinguer des points et on notera (sauf exception) $\u \cdot \v$ le produit scalaire de deux vecteurs $\vec u$ et $\vec v$ .

Le produit scalaire de deux vecteurs est donc un nombre réel, et on a, pour tous vecteurs et tous réels et :

$\langle a u_1+b u_2,v\rangle =a\langle u_1,v\rangle + b \langle u_2,v\rangle$ (linéarité à gauche)
$\langle u,a v_1+b v_2\rangle =a\langle u,v_1\rangle + b \langle u,v_2\rangle$ (linéarité à droite)
$\langle u,v\rangle =\langle v,u\rangle$ (symétrie)
$\langle u,u\rangle > 0$ pour tout vecteur non nul (positivité).

Attention : le produit scalaire de deux vecteurs n'est pas toujours positif (pour tout couple de vecteurs, les réels $\langle -u,v\rangle$ et $\langle u,v\rangle$ sont opposés).

On appellera carré scalaire d'un vecteur le produit scalaire $\langle u,u\rangle$ du vecteur par lui-même. Ce nombre est toujours positif et il est nul si et seulement si est nul.

Définition 2 On appelle espace vectoriel euclidien tout espace vectoriel réel de dimension finie muni d'un produit scalaire.

Exemples

On appelle produit scalaire canonique sur $\mathbb{R}^n$ le produit scalaire défini par :

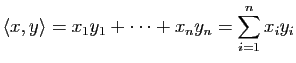
$\displaystyle \langle x,y\rangle =x_1y_1+\dots +x_ny_n=\sum_{i=1}^n x_iy_i$
si $x=(x_1,\dots,x_n)$ et $y=(y_1,\dots,y_n)$ .
En identifiant tout vecteur $x=(x_1,\dots,x_n)$ de $\mathbb{R}^n$ avec la matrice colonne de ses composantes, ce produit scalaire s'écrit encore :

$\displaystyle \langle x,y\rangle =\tr{X}Y=\tr{Y}X \; .$
Pour tout entier $n\geq 0$ et tout intervalle de $\mathbb{R}$ (), on peut définir un produit scalaire sur l'espace vectoriel $\mathbb{R}_n[X]$ des polynômes à coefficients réels de degré inférieur ou égal à par :

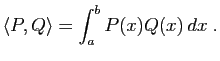
$\displaystyle \langle P,Q\rangle=\int_a^b P(x)Q(x)\, dx \; .$
Plus généralement, si est une fonction continue positive non identiquement nulle sur un intervalle de $\mathbb{R}$ (,

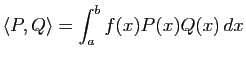
$\displaystyle \langle P,Q\rangle =\int_a^b f(x) P(x)Q(x)\, dx$
définit un produit scalaire sur $\mathbb{R}_n[X]$ .

Norme euclidienne

La positivité du produit scalaire permet de définir pour tout vecteur :

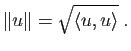
$\displaystyle \Vert u\Vert=\sqrt{\langle u,u\rangle }\; .$

Proposition 1 L'application $u\mapsto \Vert u\Vert$ est une norme sur appelée norme euclidienne sur .

Démonstration : Il faut vérifier que pour tous vecteurs et et tout réel $\lambda$ :

$\Vert\lambda u\Vert=\vert\lambda\vert \, \Vert u\Vert$ ;
$\Vert u\Vert=0 \Longleftrightarrow u=0$ ;
$\Vert u+v\Vert \leq \Vert u\Vert+\Vert v\Vert$ (inégalité triangulaire).

Les deux premières propriétés découlent immédiatement de la définition du produit scalaire. La troisième découle de l'égalité

$\displaystyle \Vert u+v\Vert^2=\Vert u\Vert^2+2\langle u,v \rangle + \Vert v\Vert^2$

et de l'inégalité de Cauchy-Schwarz $\vert\langle u,v\rangle \vert \leq \Vert u\Vert \; \Vert v\Vert$ démontrée ci-dessous. $\square$

Lemme 1 (Inégalité de Cauchy-Schwarz)

Pour tout couple de vecteurs d'un espace vectoriel euclidien, on a :

$\displaystyle \vert\langle u,v\rangle \vert \leq \Vert u\Vert \; \Vert v\Vert$

avec égalité si et seulement si et sont colinéaires.

Démonstration : Pour tout réel $\lambda$ , on a

$\displaystyle \Vert\lambda u +v\Vert^2=\lambda^2 \Vert u\Vert^2+2\lambda \langle u,v \rangle +\Vert v\Vert^2 \geq 0 \; .$

Il en résulte que, si $u\not=0$ , le discriminant de ce trinôme du second degré en $\lambda$ est négatif ou nul : $\langle u,v \rangle^2 - \Vert u\Vert^2 \Vert v\Vert^2 \leq 0$ . Ce discriminant est nul si et seulement si ce trinôme admet une racine réelle, i.e. si et seulement si il existe un réel $\lambda$ tel que $\lambda u + v=0$ . $\square$

Remarque : il résulte des démonstrations précédentes qu'on a égalité dans l'inégalité triangulaire $\Vert u+v\Vert \leq \Vert u\Vert+\Vert v\Vert$ si et seulement si $\la u,v \ra=\Vert u\Vert \, \Vert v\Vert$ , i.e. si et seulement si les deux vecteurs et sont directement colinéaires (si $u\not=0$ , il existe $\lambda\geq 0$ tel que $v=\lambda u$ ).

Définition 3 Un vecteur est dit unitaire si sa norme est égale à 1.

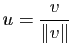À tout vecteur non nul d'un espace vectoriel euclidien, on peut associer de manière unique un vecteur unitaire qui lui est directement proportionnel en posant $u=\dfrac{v}{\Vert v\Vert}$ .

Caractérisation des normes euclidiennes

Définition 4 Une norme sur un espace vectoriel réel de dimension finie est dite euclidienne si elle provient d'un produit scalaire euclidien.

Le produit scalaire associé à une norme euclidienne est uniquement déterminé par cette norme par les relations :

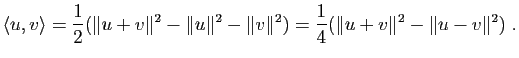
$\displaystyle \langle u,v\rangle =\dfrac{1}{2}(\Vert u+v\Vert^2-\Vert u\Vert^2-\Vert v\Vert^2)=\dfrac{1}{4}(\Vert u+v\Vert^2-\Vert u-v\Vert^2) \; .$

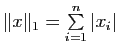Toute norme n'est pas euclidienne. Par exemple, les normes $\Vert \cdot \Vert _1$ et $\Vert\cdot \Vert _\infty$ définies sur $\mathbb{R}^n$ par $\Vert x \Vert _1=\sum\limits_{i=1}^n \vert x_i\vert$ et $\Vert x \Vert _\infty=\max\limits_{i=1,\dots,n} \vert x_i\vert$ pour $x=(x_1,\dots,x_n)$ ne sont pas euclidiennes. Elles ne vérifient en effet pas la relation du parallélogramme :

Proposition 2 Toute norme euclidienne vérifie la relation du parallélogramme :

$\displaystyle \Vert u+v\Vert^2+\Vert u-v\Vert^2=2 \, \Vert u\Vert^2+2\, \Vert v\Vert^2 \; .$

Cette relation tire son nom de ce que, si on considère le parallélogramme construit sur les deux vecteurs et , les réels $\Vert u-v\Vert$ et $\Vert u+v\Vert$ sont les longueurs des diagonales de ce parallélogramme. Elle exprime donc que la somme des carrés des longueurs des côtés d'un parallélogramme est égale à la somme des carrés des longueurs de ses diagonales.

Démonstration : Il suffit d'ajouter membre à membre les relations

$\displaystyle \Vert u+v\Vert^2=\la u+v,u+v \ra = \Vert u\Vert^2+2\la u,v \ra +\Vert v\Vert^2$

$\displaystyle \Vert u-v\Vert^2=\la u-v,u-v \ra = \Vert u\Vert^2-2\la u,v \ra +\Vert v\Vert^2 \, .$

$\square$

On peut en fait montrer que cette relation caractérise les normes euclidiennes : une norme est euclidienne si et seulement si elle vérifie l'identité du parallélogramme.