Frises et pavages

En architecture, une frise est une bande horizontale ornée d'un décor, généralement constitué par la répétition d'un même motif. Le groupe des isométries conservant une telle figure contient donc une translation dans une direction (mais pas dans deux directions, sinon la frise ne pourrait être contenue dans une bande), et par conséquent un sous-groupe de translations isomorphe à $\mathbb{Z}$.

On est ainsi amené à appeler groupe de frise un groupe d'isométries du plan dont le sous-groupe des translations est monogène, c'est-à-dire isomorphe à $\mathbb{Z}$. Si on prend un motif et si on représente les images de ce motif par toutes les isométries d'un groupe de frise, on obtient un dessin contenu dans une bande, qui se répète périodiquement comme une frise.

Un groupe de frise est un sous-groupe du groupe des isométries conservant un réseau linéaire, c'est-à-dire la figure constitué des images d'un point $A_0$ par toutes les translations de vecteur $k\vec u$, où $\vec u$ est un vecteur non nul et $k$ décrit $\mathbb{Z}$. Un tel groupe ne peut contenir que des translations de vecteur $k\vec u$ ( $k\in\mathbb{Z}$), des symétries centrales de centre situé sur la droite $D$ définie par $A_0$ et le vecteur directeur $\vec u$, des réflexions d'axe $D$ ou orthogonal à $D$, des symétries glissées d'axe $D$ et de vecteur $k \vec u /2$.

On montre plus précisément qu'il existe exactement 7 types de groupes de frise, illustrés par les figures suivantes (les transformations appartenant au groupe sont exactement celles qui laissent la frise invariante) :

De même, on appelle groupe de pavage (en anglais : wallpaper group) ou groupe cristallographique du plan un groupe d'isométries planes qui laisse invariant un réseau (i.e. un sous-groupe additif de $\mathbb{R}^2$ engendré par deux vecteurs linéairement indépendants) et contient deux translations de vecteurs linéairement indépendants.

Étant donné un tel groupe, on montre en effet qu'il existe un polygone plein (un pavé de base) tel que ses images par tous les éléments du groupe recouvrent le plan sans se chevaucher.

On montre qu'il y a 17 types de groupes de pavage. La plupart de ces groupes étaient connus depuis fort longtemps de manière empirique par les mosaïstes et les décorateurs. On peut ainsi en retrouver un grand nombre dans les mosaïques ornant l'Alhambra de Grenade (la discussion est encore ouverte parmi les historiens pour savoir si ces dix-sept groupes y sont effectivement tous représentés).

Vous pouvez télécharger aux adresses suivantes des logiciels libres vous permettant de réaliser vous-mêmes vos propres pavages ou vos propres frises :

http://www.geom.uiuc.edu/java/Kali/welcome.html

http://www.morenaments.de/

La classification complète de ces groupes est un peu fastidieuse. Une des premières étapes dans cette classification consiste à montrer que les seules rotations pouvant appartenir à un tel groupe sont d'ordre 2, 3, 4 ou 6 (i.e. ont pour angle un multiple de $\pi/2$ ou $\pi/3$). En particulier, un tel groupe ne peut contenir une rotation d'angle $2\pi/5$.

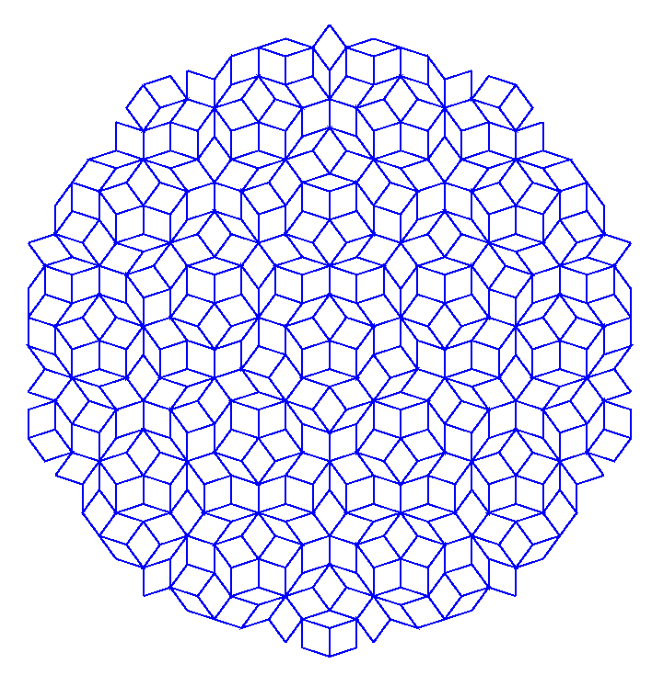
Il existe cependant des pavages du plan invariants par une rotation d'ordre 5, mais ces pavages ne sont pas périodiques. Les plus connus sont les pavages de Penrose (Roger Penrose, né en 1931, est un physicien et mathématicien britannique), dont certains sont représentés ci-dessous. Conçus au départ comme de simples jeux de l'esprit, ils sont apparus par la suite comme un modèle possible des quasi-cristaux après la découverte de ces derniers par les physiciens en 1984.