Si dans le plan il existe une infinité de polygones réguliers (pour chaque entier ![]() , il existe un polygone régulier convexe à
, il existe un polygone régulier convexe à ![]() sommets et
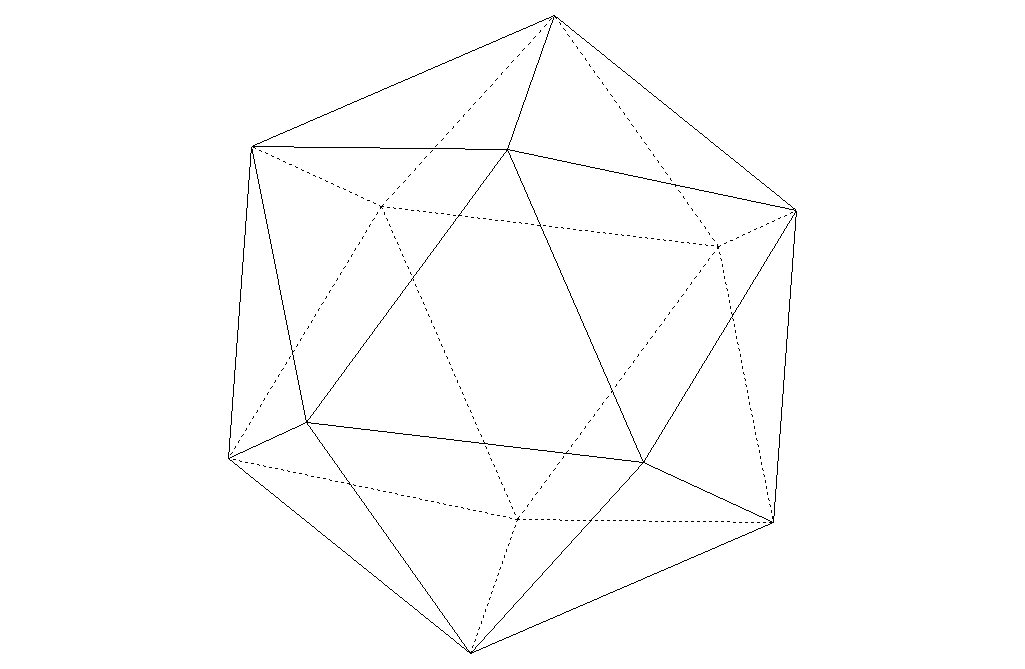
sommets et ![]() côtés, et un seul à similitude près), la situation est très différente dans l'espace. En effet il n'existe, à similitude près, que 5 types de polyèdres réguliers convexes : le tétraèdre, le cube, l'octaèdre, le dodécaèdre et l'icosaèdre. Ces polyèdres sont connus depuis l'antiquité : un dialogue de Platon, le Timée, les mentionne déjà, plus de trois siècles avant notre ère, d'où le nom de solides platoniciens qui leur est parfois donné. De nombreuses interprétations ésotériques leur ont par la suite été données au fil des siècles.
côtés, et un seul à similitude près), la situation est très différente dans l'espace. En effet il n'existe, à similitude près, que 5 types de polyèdres réguliers convexes : le tétraèdre, le cube, l'octaèdre, le dodécaèdre et l'icosaèdre. Ces polyèdres sont connus depuis l'antiquité : un dialogue de Platon, le Timée, les mentionne déjà, plus de trois siècles avant notre ère, d'où le nom de solides platoniciens qui leur est parfois donné. De nombreuses interprétations ésotériques leur ont par la suite été données au fil des siècles.
Avant de donner une indication de démonstration de ce résultat, il convient de définir ce qu'on entend par polyèdre régulier. Il ne suffit pas en effet de demander que les faces soient toutes des polygones réguliers convexes isométriques : en collant deux tétraèdres réguliers isométriques selon une face, on obtient un polyèdre dont toutes les faces sont des triangles équilatéraux isométriques, mais en 3 sommets aboutissent 4 faces, alors qu'en les 2 autres sommets n'en aboutissent que 3. Il faut donc demander de plus qu'en chaque sommet aboutissent le même nombre de faces.
Une première démonstration consiste à admettre le fait, assez intuitif, que la somme des angles des faces aboutissant en un sommet doit être strictement inférieure à ![]() .
En notant
.
En notant ![]() le nombre de sommets de chaque face et
le nombre de sommets de chaque face et ![]() le nombre d'arêtes (ou de faces) aboutissant en un sommet, on obtient alors l'inégalité
le nombre d'arêtes (ou de faces) aboutissant en un sommet, on obtient alors l'inégalité
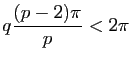
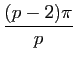 . Il en résulte facilement que les faces ne peuvent être que des triangles équilatéraux, des carrés ou des pentagones réguliers.
. Il en résulte facilement que les faces ne peuvent être que des triangles équilatéraux, des carrés ou des pentagones réguliers.
Une autre démonstration repose sur la formule d'Euler pour les polyèdres convexes : si on note ![]() le nombre de sommets,
le nombre de sommets, ![]() le nombre d'arêtes et
le nombre d'arêtes et ![]() le nombre de faces d'un tel polyèdre, Euler a remarqué que
le nombre de faces d'un tel polyèdre, Euler a remarqué que ![]() pour tout polyèdre convexe de l'espace.
pour tout polyèdre convexe de l'espace.
Chaque arête est commune à 2 faces et relie 2 sommets. On obtient ainsi, en comptant de deux manières le nombre d'arêtes, les relations
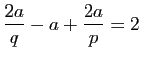
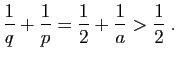
| Solide | |||
| Tétraèdre | 4 | 6 | 4 |
| Cube | 8 | 12 | 6 |
| Octaèdre | 6 | 12 | 8 |
| Dodécaèdre | 20 | 30 | 12 |
| Icosaèdre | 12 | 30 | 20 |
Une fois démontré qu'il ne peut exister plus de 5 types de polyèdres réguliers, il faut encore les construire. C'est élémentaire pour le cube, le tétraèdre et l'octaèdre, un peu moins pour le dodécaèdre et l'icosaèdre.
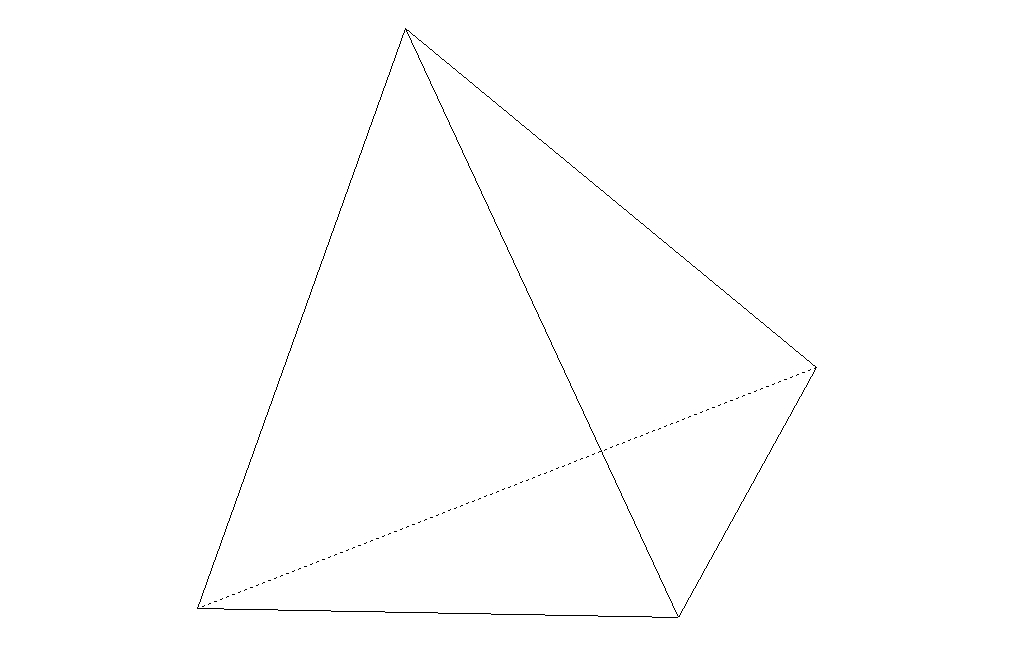
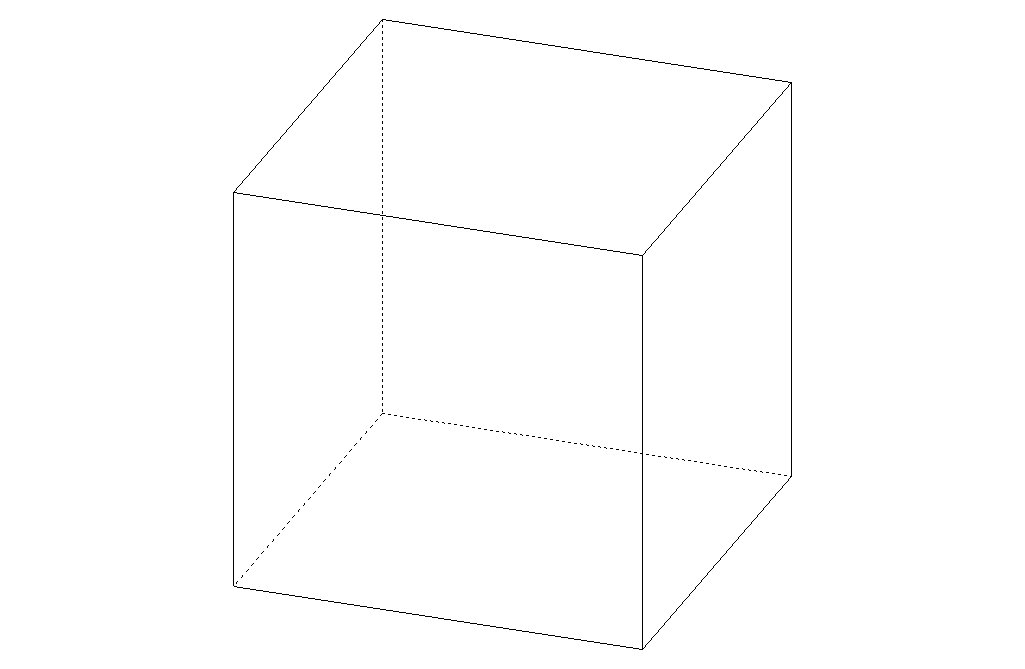
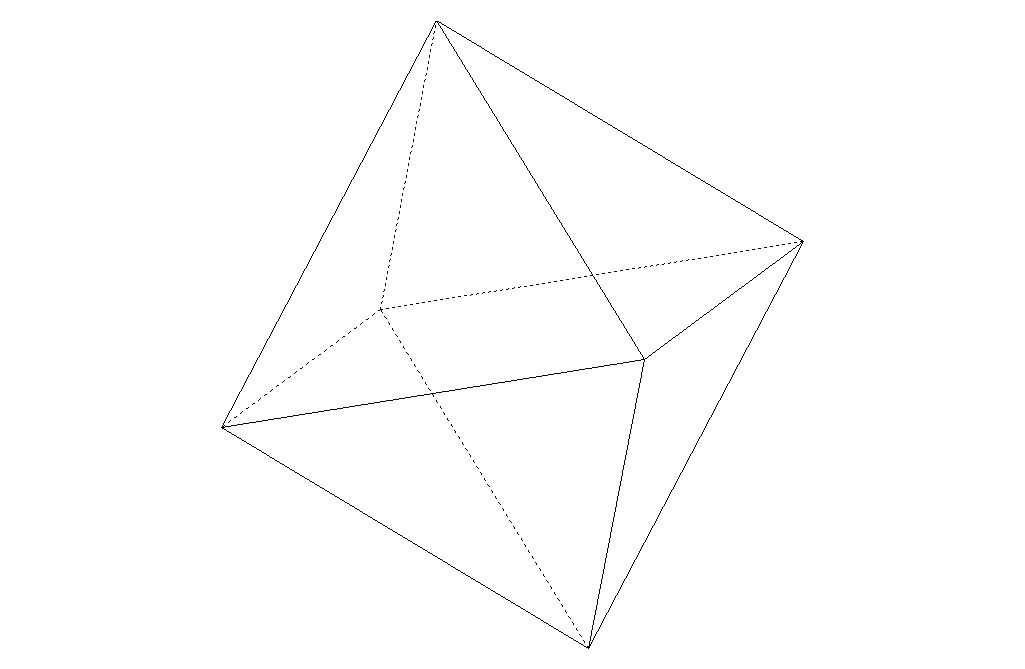
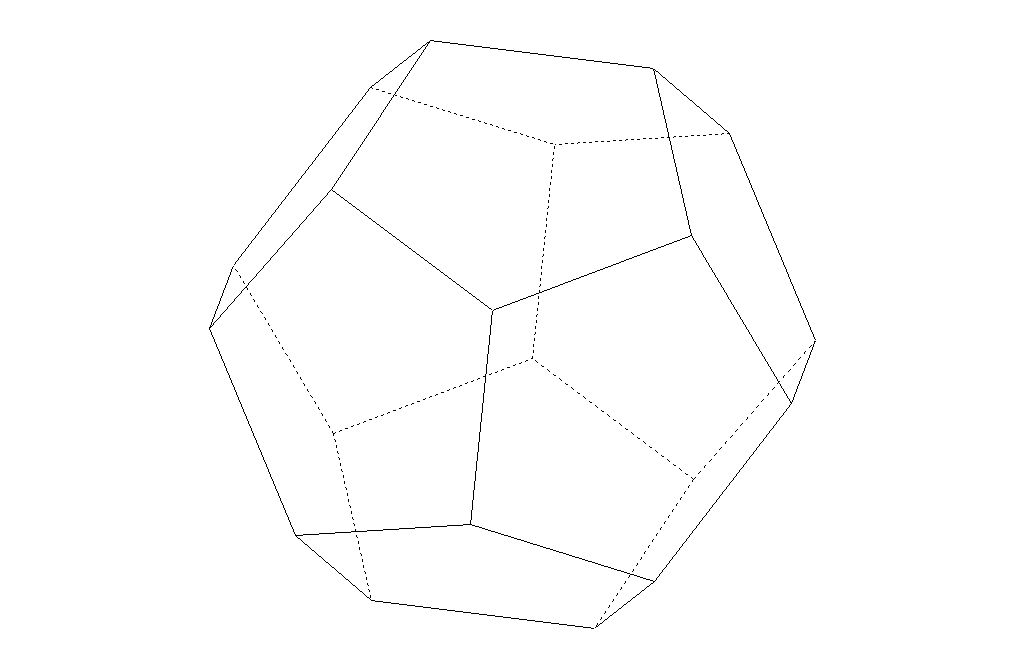
On remarque que ![]() et
et ![]() jouent des rôles symétriques dans les formules précédentes, ainsi que
jouent des rôles symétriques dans les formules précédentes, ainsi que ![]() et
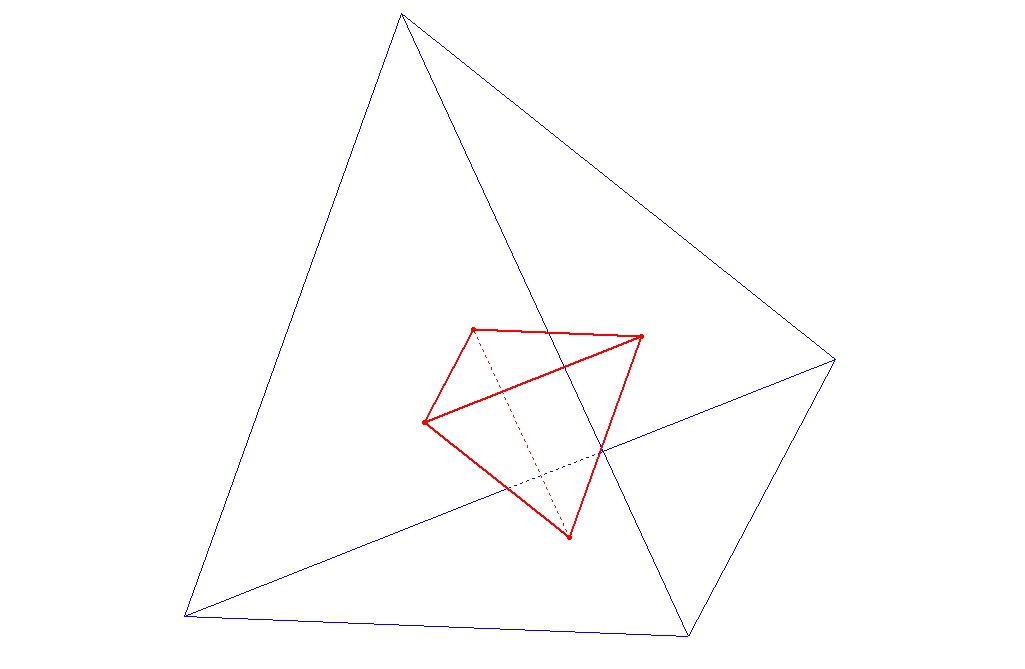
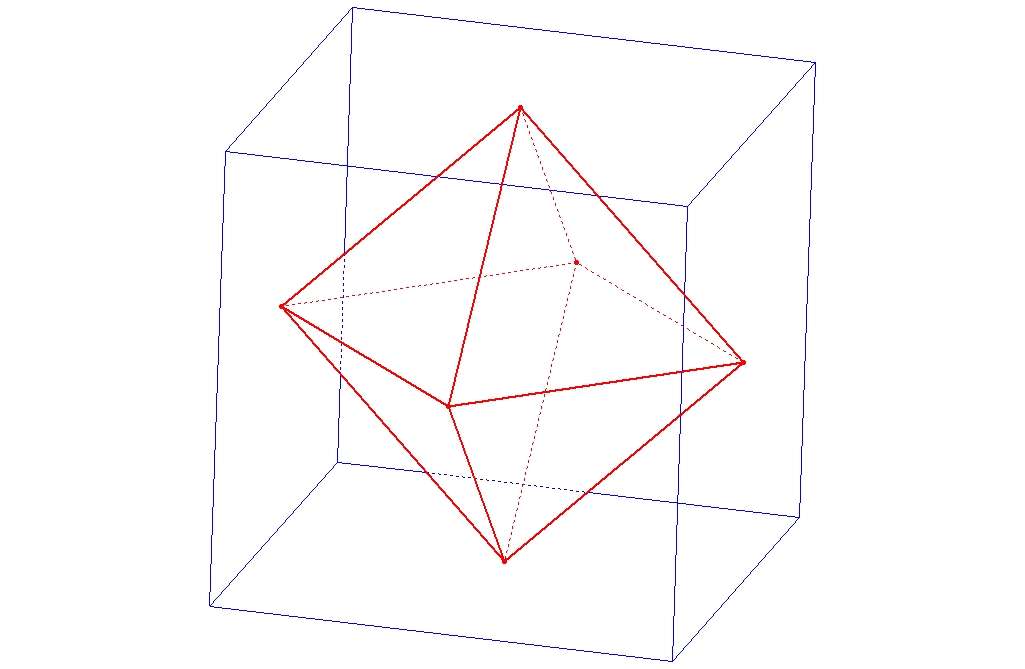
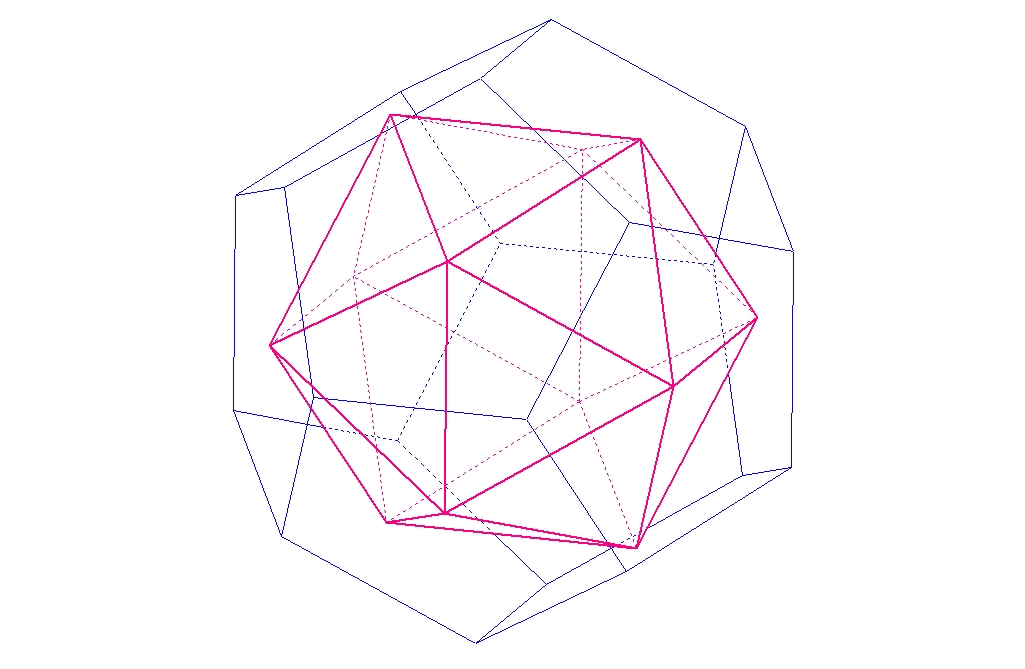
et ![]() . Géométriquement, cette remarque s'interprète de la façon suivante : les centres des faces d'un de ces polyèdres réguliers sont les sommets d'un autre polyèdre régulier, et en réitérant l'opération on retombe sur un polyèdre homothétique au polyèdre de départ. On obtient ainsi une dualité entre les polyèdres réguliers, le cube étant dual de l'octaèdre et l'icosaèdre du dodécaèdre, le tétraèdre étant quant à lui son propre dual.
. Géométriquement, cette remarque s'interprète de la façon suivante : les centres des faces d'un de ces polyèdres réguliers sont les sommets d'un autre polyèdre régulier, et en réitérant l'opération on retombe sur un polyèdre homothétique au polyèdre de départ. On obtient ainsi une dualité entre les polyèdres réguliers, le cube étant dual de l'octaèdre et l'icosaèdre du dodécaèdre, le tétraèdre étant quant à lui son propre dual.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales