Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
- Rappeler la définition de l'orthogonal d'une partie d'un espace vectoriel euclidien . Donner une relation entre les dimensions d'un et de son orthogonal.
- Rappeler les définitions du produit mixte et du produit vectoriel dans un espace vectoriel euclidien orienté de dimension 3. Donner une condition nécessaire et suffisante sur deux vecteurs pour que la norme de leur produit vectoriel soit nulle (resp. égale au produit de leurs normes).
- Énoncer le théorème de diagonalisation des endomorphismes symétriques d'un espace vectoriel euclidien . Caractériser la plus grande et la plus petite valeur propre d'un endomorphisme symétrique
 d'un tel espace
d'un tel espace  en fonction des produits scalaires
en fonction des produits scalaires
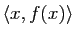 pour
pour 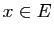 .
.
- Soient
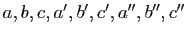 des réels. Montrer l'équivalence des deux propriétés :
des réels. Montrer l'équivalence des deux propriétés :
et
- Donner l'écriture complexe d'une similitude directe du plan complexe. Déterminer les éléments caractéristiques (rapport, angle, points fixes) d'une similitude directe donnée sous forme complexe.
Exercice 1 :
Soit  et
et 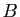 deux points distincts du plan affine euclidien
deux points distincts du plan affine euclidien  et
et 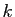 un réel strictement positif différent de 1. On se propose d'étudier l'ensemble
un réel strictement positif différent de 1. On se propose d'étudier l'ensemble 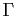 des points
des points 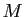 de
de  vérifiant
vérifiant
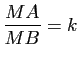 :
:
- Montrer qu'un point
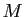 du plan appartient à
du plan appartient à 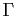 les vecteurs
les vecteurs
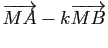 et
et
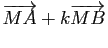 sont orthogonaux.
sont orthogonaux.
- Montrer qu'il existe un point
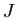 (resp.
(resp. 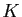 ) du plan et un seul tel que
) du plan et un seul tel que
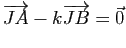 (resp.
(resp.
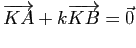 ). Exprimer, pour tout point
). Exprimer, pour tout point 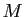 du plan, le vecteur
du plan, le vecteur
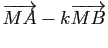 (resp.
(resp.
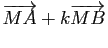 ) en fonction du vecteur
) en fonction du vecteur 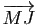 (resp.
(resp. 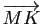 ).
).
- En déduire que
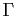 est un cercle dont on précisera le centre.
est un cercle dont on précisera le centre.
- Soit
 le barycentre du système pondéré
le barycentre du système pondéré
![$ [(A,1),\, (B,-k^2)]$](img1359.gif) . Exprimer, pour tout point
. Exprimer, pour tout point 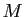 du plan,
du plan,
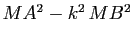 en fonction de
en fonction de 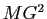 ,
, 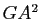 et
et 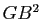 . Retrouver ainsi le résultat de la question précédente.
. Retrouver ainsi le résultat de la question précédente.
- Montrer que la puissance
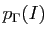 du milieu
du milieu 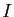 de
de ![$ [AB]$](img599.gif) par rapport au cercle
par rapport au cercle 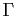 est égale à
est égale à 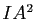 . En déduire que le cercle
. En déduire que le cercle 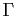 et le cercle de diamètre
et le cercle de diamètre ![$ [AB]$](img599.gif) sont orthogonaux.
sont orthogonaux.
- Montrer que tout cercle passant par les deux points
 et
et 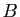 est orthogonal à
est orthogonal à 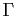 .
.
Exercice 2 :
Le but de cet exercice est d'étudier le groupe des isométries du tétraèdre régulier et en particulier de montrer que ce groupe est isomorphe au groupe
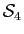 des permutations de quatre éléments. On considère donc un tétraèdre régulier
des permutations de quatre éléments. On considère donc un tétraèdre régulier 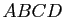 de l'espace affine euclidien
de l'espace affine euclidien  de dimension 3 et on note
de dimension 3 et on note  le groupe des isométries de
le groupe des isométries de  laissant globalement invariant l'ensemble
laissant globalement invariant l'ensemble
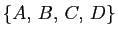 des sommets de ce tétraèdre. On note
des sommets de ce tétraèdre. On note 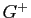 le sous-ensemble de
le sous-ensemble de  constitué des isométries directes et
constitué des isométries directes et 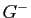 le sous-ensemble de
le sous-ensemble de  constitué des isométries indirectes.
constitué des isométries indirectes.
- Montrer qu'il existe un point
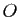 de
de  fixe par tout élément de
fixe par tout élément de  .
.
- Montrer que tout élément
 de
de  induit une permutation
induit une permutation
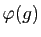 des sommets du tétraèdre et que l'application
des sommets du tétraèdre et que l'application 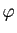 ainsi définie est un homomorphisme injectif du groupe
ainsi définie est un homomorphisme injectif du groupe  dans le groupe
dans le groupe
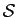 des permutations de ces sommets.
des permutations de ces sommets.
- Soit
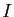 le milieu du segment
le milieu du segment ![$ [AB]$](img599.gif) . Montrer que le plan
. Montrer que le plan 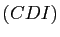 est le plan médiateur de
est le plan médiateur de ![$ [AB]$](img599.gif) . En déduire qu'il existe dans
. En déduire qu'il existe dans  une réflexion échangeant les points
une réflexion échangeant les points  et
et 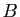 et laissant fixes
et laissant fixes 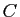 et
et 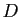 .
.
- Montrer que l'image
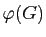 de
de 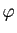 contient toutes les transpositions des sommets. En déduire que
contient toutes les transpositions des sommets. En déduire que 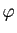 est surjectif. On rappelle qu'une transposition est une permutation échangeant deux éléments et laissant les autres fixes et que les transpositions engendrent le groupe symétrique.
est surjectif. On rappelle qu'une transposition est une permutation échangeant deux éléments et laissant les autres fixes et que les transpositions engendrent le groupe symétrique.
- En déduire les cardinaux de
 ,
, 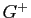 et
et 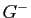 et montrer que l'image
et montrer que l'image
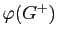 de
de 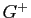 par
par 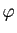 est égale au groupe alterné (sous-groupe de
est égale au groupe alterné (sous-groupe de
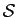 constitué des permutations de signature +1).
constitué des permutations de signature +1).
- Montrer que tous les éléments de
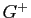 autres que l'identité sont des rotations. Préciser les axes et les angles de ces rotations.
autres que l'identité sont des rotations. Préciser les axes et les angles de ces rotations.
- Montrer que
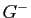 contient exactement 6 réflexions dont on précisera les plans. Donner la nature géométrique et l'ordre dans le groupe
contient exactement 6 réflexions dont on précisera les plans. Donner la nature géométrique et l'ordre dans le groupe  des autres éléments de
des autres éléments de 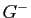 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
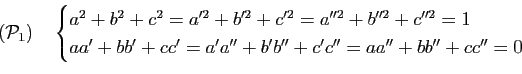
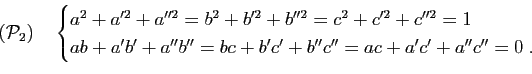
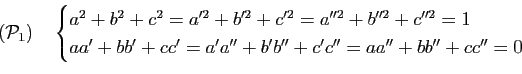
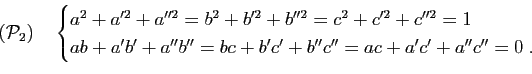
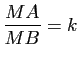 :
:
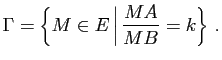
![]() des permutations de quatre éléments. On considère donc un tétraèdre régulier
des permutations de quatre éléments. On considère donc un tétraèdre régulier ![]() de l'espace affine euclidien
de l'espace affine euclidien ![]() de dimension 3 et on note
de dimension 3 et on note ![]() le groupe des isométries de
le groupe des isométries de ![]() laissant globalement invariant l'ensemble
laissant globalement invariant l'ensemble
![]() des sommets de ce tétraèdre. On note
des sommets de ce tétraèdre. On note ![]() le sous-ensemble de
le sous-ensemble de ![]() constitué des isométries directes et
constitué des isométries directes et ![]() le sous-ensemble de
le sous-ensemble de ![]() constitué des isométries indirectes.
constitué des isométries indirectes.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales