Section : Entraînement
Avant : Devoir
Après : Compléments

Corrigé du devoir

Questions de cours :  
  1. L'orthogonal d'une partie $ A$ d'un espace vectoriel euclidien $ E$ est l'ensemble des vecteurs de $ E$ orthogonaux à tout vecteur de $ A$ :

    $\displaystyle A^\perp=\{u\in E \mid \la u,x \ra=0 \quad \forall x \in A \} \; .$

    C'est un sous-espace vectoriel de $ E$.

    Si $ F$ est un sous-espace vectoriel de $ E$, on a $ \dim (F^\perp)=\dim (E) - \dim (F)$.

  2. Le produit mixte $ \mathrm{det}(u,v,w)$ de trois vecteurs $ u$, $ v$, $ w$ d'un espace vectoriel euclidien orienté de dimension 3 est le déterminant de ces trois vecteurs évalué dans une base orthonormée directe (ce déterminant ne dépend pas du choix d'une telle base).

    Le produit vectoriel de deux vecteurs $ u$ et $ v$ d'un tel espace $ E$ est l'unique vecteur $ u\wedge v$ vérifiant $ \mathrm{det}(u,v,x)=\la u\wedge v,x \ra$ pour tout vecteur $ x$ de $ E$.

  3. Pour tout endomorphisme symétrique $ f$ d'un espace vectoriel euclidien $ E$, il existe une base orthonormée de $ E$ constituée de vecteurs propres de $ f$. La matrice de $ f$ dans une telle base est donc diagonale.

    La plus grande et la plus petite des valeurs propres de $ f$ sont données par 

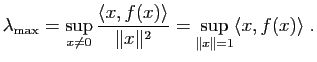
    $\displaystyle \lambda_{\mathrm{max}}=\sup\limits_{x\not = 0} \dfrac{\la x,f(x) \ra}{\Vert x\Vert^2} =\sup\limits_{ \Vert x\Vert =1} \la x,f(x) \ra \;.$

    resp.

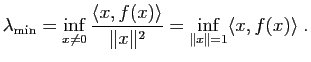
    $\displaystyle \lambda_{\mathrm{min}}=\inf\limits_{x\not = 0} \dfrac{\la x,f(x) \ra}{\Vert x\Vert^2} =\inf\limits_{ \Vert x\Vert =1} \la x,f(x) \ra \;.$

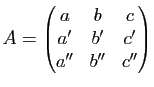  4. Soit $ A$ la matrice  $ A=\begin{pmatrix} a & b & c\\ a' & b' & c'\\ a'' & b'' & c'' \end{pmatrix}$. Les relations $ \mathcal P_1$ (resp. $ \mathcal P_2$) expriment que $ A\tr{A}=I_3$ (resp. $ \tr{A}A=I_3$). Elles sont donc vérifiées si et seulement si $ A$ est inversible et a pour inverse sa transposée, i.e. si et seulement si $ A$ est orthogonale, et sont donc équivalentes.

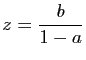  5. Toute similitude directe du plan complexe s'écrit sous la forme $ z\mapsto az+b$ pour un nombre complexe $ b$ et un nombre complexe non nul $ a$. Le rapport d'une telle similitude est $ \vert a\vert$ et son angle $ \Arg(a)$. Elle admet comme unique point fixe $ z=\dfrac{b}{1-a}$ si $ a\not =1$. Si $ a=1$ et $ b\not =0$, la similitude est une translation de vecteur non nul et n'admet pas de point fixe. Si $ a=1$ et $ b=0$, c'est l'identité et tout point est fixe.
Exercice 1 :
  1. Un point $ M$ de $ E$ appartient à $ \Gamma$ $ MA^2-k^2 MB^2=0$, soit encore $ (\vv{MA}-k\vv{MB}) \cdot (\vv{MA}+k\vv{MB})=0$.

  2. L'égalité $ \vv{JA}-k\vv{JB}=\0$ signifie que $ J$ est le barycentre du système pondéré $ [(A,1),\, (B,-k)]$. Ce barycentre existe et est unique puisque $ 1-k \not = 0$. On a alors, pour tout point $ M$ de $ E$ :

    $\displaystyle \vv{MA}-k\vv{MB}=(\vv{MJ}+\vv{JA})-k (\vv{MJ}+\vv{JB})=(1-k) \vv{MJ} \, .$

    De même, le point $ K$ est le barycentre du système pondéré $ [(A,1),\, (B,k)]$ et on a, pour tout point $ M$ de $ E$ :

    $\displaystyle \vv{MA}+k\vv{MB}=(\vv{MK}+\vv{KA})+k (\vv{MK}+\vv{KB})=(1+k) \vv{MK} \, .$

  3. L'orthogonalité des vecteurs $ \vv{MA}-k\vv{MB}$ et $ \vv{MA}+k\vv{MB}$ équivaut donc à l'orthogonalité des vecteurs $ \vv{MJ}$ et $ \vv{MK}$. Un point $ M$ de $ E$ appartient à $ \Gamma$ ces vecteurs sont orthogonaux, on en déduit que $ \Gamma$ est le cercle de diamètre $ [JK]$. Son centre est le milieu de ce segment et appartient donc à la droite $ (AB)$, puisque ces deux points sont situés sur cette droite ($ K$ appartient au segment $ [AB]$ et $ J$ au complémentaire de ce segment dans la droite).
  4. Le barycentre du système pondéré $ [(A,1),\, (B,-k^2)]$ est bien défini puisque $ 1-k^2 \not =0$. On a :

    $\displaystyle MA^2-k^2 \, MB^2$ $\displaystyle = (\vv{MG}+\vv{GA})^2-k^2 \, (\vv{MG}+\vv{GB})^2$    
      $\displaystyle =MG^2+2 \, \vv{MG}\cdot\vv{GA}+GA^2 -k^2 \, (MG^2+2 \, \vv{MG}\cdot\vv{GB}+GB^2)$    
      $\displaystyle =(1-k^2) \, MG^2+GA^2-k^2 \, GB^2$    

    puisque $ \vv{GA}-k^2 \, \vv{GB}=\0$.

    Un point $ M$ de $ E$ appartient à $ \Gamma$ $ MA^2-k^2 \, MB^2 =0$, i.e.

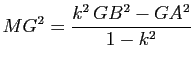
    $\displaystyle MG^2=\dfrac{k^2 \, GB^2-GA^2}{1-k^2}$

    ce qui montre que $ \Gamma$ est un cercle de centre $ G$ ($ \Gamma$ n'est pas vide puisqu'il contient les deux points $ J$ et $ K$). On pouvait vérifier directement que $ G$ est le milieu du segment $ [JK]$, cette propriété découle aussi des deux dernières questions.
  5. La puissance $ p_\Gamma(I)$ du milieu $ I$ de $ [AB]$ par rapport au cercle $ \Gamma$ est égale à $ \vv{IJ}\cdot \vv{IK}$, puisque la droite $ (AB)$ coupe le cercle $ \Gamma$ en $ J$ et $ K$.

    En faisant $ M=I$ dans le résultat de la question 2, on obtient les relations

    $\displaystyle (1-k) \, \vv{IJ}$ $\displaystyle =\vv{IA}-k \, \vv{IB}$    
    $\displaystyle (1+k) \, \vv{IK}$ $\displaystyle =\vv{IA}+k \, \vv{IB} \, .$    

    Il en résulte

    $\displaystyle (1-k^2) \, \vv{IJ}\cdot \vv{IK}$ $\displaystyle =(\vv{IA}-k \, \vv{IB}) \cdot (\vv{IA}+k \, \vv{IB})$    
      $\displaystyle =IA^2-k^2 \, IB^2$    
      $\displaystyle =(1-k^2) \, IA^2$    

    puisque $ IA=IB$, d'où $ p_\Gamma(I)=IA^2$, ce qui montre que le cercle $ \Gamma$ et le cercle de diamètre $ [AB]$ sont orthogonaux.
  6. La puissance du centre $ G$ du cercle $ \Gamma$ par rapport au cercle de diamètre $ [AB]$ est égale au carré $ R^2$ du rayon de $ \Gamma$, puisque ces deux cercles sont orthogonaux. Mais la puissance de $ G$ par rapport à tout cercle passant par les deux points $ A$ et $ B$ est égale à la puissance de $ G$ par rapport au cercle de diamètre $ [AB]$, puisqu'elle vaut $ \vv{GA}\cdot \vv{GB}$. Il en résulte que $ \Gamma$ est orthogonal à tout cercle passant par $ A$ et $ B$.

    \includegraphics[width=0.9\textwidth]{devoir1}


Exercice 2 :

  1. L'isobarycentre $ O$ des sommets $ A$, $ B$, $ C$, $ D$ du tétraèdre est fixe par tout élément de $ G$, puisqu'une isométrie est une transformation affine et qu'une transformation affine conserve les barycentres.

  2. Tout élément de $ G$ permute les sommets du tétraèdre et induit donc une permutation de l'ensemble $ \{A,B,C,D\}$. L'application $ \varphi$ qui associe à tout élément de $ G$ sa restriction à l'ensemble $ \{A,B,C,D\}$ est un homomorphisme du groupe $ G$ dans le groupe $ \mathcal S$ des permutations de ces sommets. Cet homorphisme est injectif, puisque $ (A,B,C,D)$ constitue un repère affine de $ E$ et qu'une transformation affine est entièrement déterminée par les images des points d'un repère affine.

  3. Le tétraèdre $ ABCD$ étant régulier, on a $ CA=CB$ et $ DA=DB$, ce qui montre que $ C$ et $ D$ appartiennent au plan médiateur du segment $ [AB]$. Le milieu $ I$ de $ [AB]$ appartient également à ce plan. Les trois points $ C,D,I$ ne sont pas alignés et déterminent donc un plan, qui est le plan médiateur de $ [AB]$. Ce plan est perpendiculaire en $ I$ à la droite $ (AB)$ et la symétrie orthogonale par rapport à ce plan échange les points $ A$ et $ B$. Elle laisse fixe les points $ C$ et $ D$ et a donc comme image par $ \varphi$ la transposition échangeant $ A$ et $ B$.

  4. En procédant de même avec les autres arêtes du tétraèdre, on voit que $ G$ contient 6 réflexions de plans les plans médiateurs des 6 arêtes, dont les images par $ \varphi$ sont les 6 transpositions que contient le groupe $ \mathcal S$. Ces transpositions engendrent le groupe $ \mathcal S$. Comme l'image $ \varphi (G)$ du groupe $ G$ par l'homomorphisme de groupes $ \varphi$ est un sous-groupe de $ \mathcal S$, cette image est égale à $ \mathcal S$. L'homomorphisme $ \varphi$ est donc surjectif ; comme il est injectif, c'est un isomorphisme de $ G$ sur $ \mathcal S$.

  5. Il en résulte que $ G$, étant en bijection avec $ \mathcal S$, a même cardinal que $ \mathcal S$, i.e. 4!=24. $ G$ est réunion disjointe de $ G^+$ et de $ G^-$ et ces deux ensembles ont le même nombre d'éléments : en effet $ G^-$ n'est pas vide, puisqu'il contient les 6 réflexions précédemment trouvées et l'application $ g\mapsto s\circ g$, où $ s$ est l'une quelconque de ces réflexions, est une bijection de $ G^+$ sur $ G^-$. Il en résulte que $ G^+$ et $ G^-$ ont tous deux 12 éléments.

  6. Les éléments de $ G^+$ autres que l'identité sont des déplacements de $ E$ ayant un point fixe $ O$, donc des rotations d'axes passant par $ O$. Pour chaque sommet du tétraèdre, la perpendiculaire à la face opposée à ce sommet passant par ce sommet rencontre la face opposée au centre de gravité de cette face. Les rotations d'angles $ \pm \dfrac{2\pi}{3}$ autour de cet axe appartiennent donc à $ G$. Leurs images par $ \varphi$ sont les 8 cycles de longueur 3 que contient $ \mathcal S$. Par ailleurs, les demi-tours d'axes les bimédianes du tétraèdres (droites joigant les milieux de deux arêtes opposées) appartiennent à $ G$, puisque ces bimédianes sont perpendiculaires aux arêtes dont elles joignent les milieux (par exemple si $ J$ est le milieu de $ [CD]$, la droite $ (IJ)$ est incluse à la fois dans le plan médiateur de $ [AB]$ et dans le plan médiateur de $ [CD]$). On obtient ainsi 3 demi-tours d'axes les 3 bimédianes, dont les images par $ \varphi$ sont les 3 produits de deux transpositions de supports disjoints que contient $ \mathcal S$. Le groupe $ G^+$ des déplacements conservant le tétraèdre contient donc 8 éléments d'ordre 3, 3 éléments d'ordre 2 et un élément d'ordre 1 (l'identité).

  7. On a déjà vu que $ G^-$ contenait 6 réflexions de plans les plans médiateurs des arêtes du tétraèdre. L'image par $ \varphi$ d'une réflexion est un élément d'ordre 2 de $ \mathcal S$, c'est-à-dire une transposition ou un produit de deux transpositions de supports disjoints. $ G$ ne peut donc contenir d'autre réflexions que les 6 déjà trouvées. Les autres éléments de $ G$ sont donc des antirotations d'axes et de plans passant par $ O$. Ils ont pour images par $ \varphi$ les 6 permutations circulaires des quatre sommets et sont donc d'ordre 4 dans $ G$. Si $ s\circ r=r \circ s$ est la décomposition canonique d'une telle antirotation, avec $ s$ une réflexion et $ r$ une rotation d'axe perpendiculaire au plan de la réflexion, $ (s\circ r)^2=r^2$ doit être un élément d'ordre 2 de $ G^+$, i.e. un des trois demi-tours d'axes les bimédianes. La rotation $ r$ a donc pour axe une bimédiane et pour angle $ \pm \dfrac{\pi}{2}$ et le plan de $ s$ est le plan perpendiculaire en $ O$ à cette bimédiane, i.e. le plan médiateur du segment joignant les milieux de deux arêtes opposées (ce plan contient les milieux des 4 autres arêtes).

Section : Entraînement
Avant : Devoir
Après : Compléments


         © UJF Grenoble, 2011                              Mentions légales