-
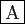
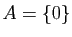 si et seulement si
si et seulement si 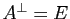 .
.
-
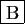
-
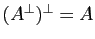 .
.
-
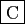
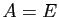 si et seulement si
si et seulement si
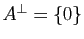 .
.
-
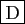
- Si
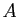 est un sous-espace vectoriel de
est un sous-espace vectoriel de 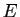 , alors
, alors
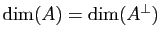 .
.
-
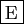
-
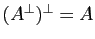 si et seulement si
si et seulement si 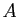 est un sous-espace vectoriel de
est un sous-espace vectoriel de 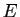 .
.
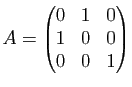 ;
;
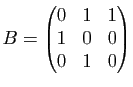 ;
;
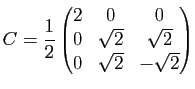 ;
;
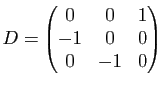 ;
;
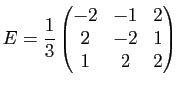 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales