Exercices

Exercice 1 Soit un espace vectoriel euclidien de dimension , $(e_1,\dots,e_n)$ une base orthonormale de , un hyperplan vectoriel de d'équation $\,a_1x_1+\cdots +a_nx_n = 0\,$ dans cette base. Donner la matrice dans la base $(e_1,\ldots ,e_n)$ des projections orthogonales sur $H^\perp$ et sur .

Exercice 2 1) Soit un vecteur non nul d'un espace vectoriel euclidien de dimension . Exprimer en fonction de et le projeté orthogonal d'un vecteur de sur l'hyperplan orthogonal à .

2) Soient $v_0,v_1,\dots , v_m$ vecteurs de vérifiant $\langle v_i,v_j\rangle <0$ pour tout couple d'indices distincts. Montrer que les projetés orthogonaux $v'_1,\dots, v'_m$ des vecteurs $v_1,\dots, v_m$ sur l'hyperplan orthogonal à vérifient $\langle v'_i,v'_j\rangle <0$ pour tout couple d'indices distincts.

3) En déduire par récurrence sur que $m\leq n$ .

4) Montrer qu'il existe vecteurs $v_0,v_1,\dots , v_n$ de vérifiant $\langle v_i,v_j\rangle <0$ pour tout couple d'indices distincts. La borne dans l'inégalité de la question précédente ne peut donc pas être améliorée.

Exercice 3 Soient et deux sous-espaces vectoriels d'un espace vectoriel euclidien . Montrer que les trois propriétés suivantes sont équivalentes:

(i): $F^\perp \subset G$ ;
(ii): $G^\perp \subset F$ ;
(iii): $F^\perp$ et $G^\perp$ sont orthogonaux.

Exercice 4 Soit et deux sous-espaces vectoriels d'un espace vectoriel euclidien tels que $F\subset G$ , et les projections orthogonales sur et . Montrer que $p_F \circ p_G=p_F$ .

Exercice 5 Soit trois vecteurs d'un espace vectoriel euclidien orienté de dimension 3. Montrer que que la famille est libre si et seulement si la famille $(u\wedge v, u\wedge w)$ est libre.

Exercice 6 Soit, dans un espace vectoriel euclidien , une tranformation orthogonale et un sous-espace vectoriel de tels que . Montrer que $f(F^\perp)=F^\perp$ .

Exercice 7 Soit, dans un plan vectoriel euclidien, une rotation vectorielle et une réflexion vectorielle .

1) Déterminer $s \circ r \circ s$ et $r \circ s \circ r$ .

2) Donner une condition nécessaire et suffisante pour que et commutent.

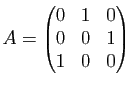Exercice 8 Soit, dans un espace vectoriel euclidien de dimension 3 rapporté à une base orthonormée, l'endomorphisme de matrice $A=\begin{pmatrix} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end{pmatrix}$ . Montrer que est une rotation vectorielle dont on précisera l'axe et l'angle.

Exercice 9 Soit, dans un espace vectoriel euclidien de dimension 3 rapporté à une base orthonormée, l'endomorphisme de matrice $\begin{pmatrix}0&1&0\\ 0&0&1\\ -1&0&0\end{pmatrix}$ . Montrer que est une antirotation dont on déterminera l'axe et l'angle.

Exercice 10 Dans un espace vectoriel euclidien de dimension 3, déterminer le produit de deux demi-tours. Montrer que toute rotation vectorielle peut s'écrire comme produit de deux demi-tours. Cette écriture est-elle unique ?

Exercice 11 1) Soit, dans un espace vectoriel euclidien de dimension 3, une réflexion vectorielle de plan , une rotation vectorielle d'axe et un vecteur directeur de 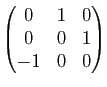. Montrer que si $s\circ r=r \circ s$ , alors $s(u)=\pm u$ et .

2) Donner une condition nécessaire et suffisante pour qu'une rotation vectorielle et une réflexion vectorielle commutent.

Exercice 12 On se place dans un espace vectoriel euclidien de dimension 3.

1) Soient et deux rotations vectorielles de même axe. Montrer que $r_1\circ r_2=r_2\circ r_1$ .

2) Soient et deux demi-tours d'axes et orthogonaux. Montrer que $r_1\circ r_2=r_2\circ r_1$ et déterminer cette rotation.

3) Soit une rotation différente de l'identité, et son axe. Soit $\Delta$ une droite vectorielle distincte de telle que $r(\Delta)=\Delta$ . Montrer que et $\Delta$ sont orthogonales et que est un demi-tour.

4) Soient et deux rotations vectorielles distinctes de l'identité d'axes et distincts. On suppose $r_1\circ r_2=r_2\circ r_1$ . Montrer que . En déduire que et sont deux demi-tours d'axes orthogonaux.

5) Donner une condition nécessaire et suffisante pour que deux rotations vectorielles commutent.

Exercice 13 1) Soit un endomorphisme d'un espace vectoriel euclidien . Montrer que les propriétés suivantes sont équivalentes :

(i): $\langle x,f(x)\rangle \; =0$ pour tout vecteur de ;
(ii): $\langle f(x),y\rangle \; =-\langle x,f(y)\rangle$ pour tout couple de vecteurs de ;
(iii): la matrice de dans toute base orthonormale de est antisymétrique ;
(iv): il existe une base orthonormale de dans laquelle la matrice de est antisymétrique ;
(v): .

Un endomorphisme vérifiant ces propriétés est dit antisymétrique.

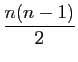2) Montrer que l'ensemble des endomorphismes antisymétriques d'un espace vectoriel euclidien de dimension est un sous-espace vectoriel $\mathcal A$ de dimension $\dfrac{n(n-1)}{2}$ de l'espace vectoriel $\mathcal L$ des endomorphismes de .

3) Soit $\mathcal S$ l'espace des endomorphismes symétriques de . Montrer que les sous-espaces vectoriels $\mathcal S$ et $\mathcal A$ sont supplémentaires dans $\mathcal L$ . Écrire la décomposition d'un endomorphisme de suivant ces deux sous-espaces.

4) Montrer que le noyau et l'image d'un endomorphisme antisymétrique sont des sous-espaces vectoriels supplémentaires orthogonaux.

5) Montrer que le déterminant de tout endomorphisme antisymétrique d'un espace vectoriel euclidien de dimension impaire est nul.

6) Déduire des deux questions précédentes que le rang d'un endomorphisme antisymétrique est toujours pair (on pourra considérer la restriction de cet endomorphisme à son image).

7) Décrire les endomorphismes antisymétriques d'un espace vectoriel euclidien de dimension 2.

8) Soit un endomorphisme antisymétrique d'un espace vectoriel euclidien orienté de dimension 3. Montrer qu'il existe un vecteur de et un seul tel que $f(x)=v\wedge x$ pour tout vecteur de . Exprimer le noyau et l'image de en fonction de .

9) Soient et deux vecteurs d'un espace vectoriel euclidien orienté de dimension 3. Discuter en fonction de et l'existence et le nombre de solutions de l'équation $u\wedge x=v$ .

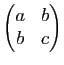Exercice 14 Montrer qu'une matrice réelle carrée d'ordre 2 symétrique $\begin{pmatrix} a&b\\ b&c \end{pmatrix}$ est définie positive si et seulement si et .

Exercice 15 On identifie, dans tout cet exercice, toute matrice réelle à lignes et colonnes à l'application linéaire de $\mathbb{R}^p$ dans $\mathbb{R}^n$ qui lui est associée. On identifie également tout vecteur de $\mathbb{R}^p$ à la matrice colonne de ses composantes.

1) Soit une matrice à lignes et colonnes et un vecteur de $\mathbb{R}^p$ . Exprimer $^t\!X \, ^t\!M M X$ en fonction de la norme euclidienne de .

2) Montrer que la matrice $^t\! M M$ est symétrique positive.

3) Comparer les noyaux, puis les rangs, de et $^t\! M M$ .

4) Montrer que $^t\! M M$ est définie positive si et seulement si les vecteurs colonnes de sont linéairement indépendants.

Exercice 16 Matrice de Gram

Soit un espace vectoriel euclidien de dimension et $v_1,\ldots ,v_p$ une famille de vecteurs de . On appelle matrice de Gram de $(v_1,\ldots ,v_p)$ la matrice Gram $(v_1,\ldots ,v_p)=(g_{i,j})_{i,j=1\ldots p}$ de coefficients

$\displaystyle g_{i,j} = \la v_i,v_j \ra$

et déterminant de Gram de cette famille le déterminant

$\displaystyle G(v_1,\ldots ,v_p)=\mathrm{det}\left(\mbox{Gram}(v_1,\ldots ,v_p)\right)$

de sa matrice de Gram.

1) Soit $(e_1,\dots,e_n)$ une base orthonormale de et la matrice des vecteurs $(v_1,\ldots ,v_p)$ dans cette base. Montrer que Gram $(v_1,\ldots ,v_p)=\, ^t\!M M$ . En déduire que $G(v_1,\ldots ,v_p)\geq 0$ .

2) Montrer que les vecteurs $v_1,\ldots ,v_p$ sont linéairement indépendants si et seulement si $G(v_1,\ldots ,v_p) > 0$ .

3) Soient $a\in E$ , un sous-espace vectoriel de et $(w_1,\ldots ,w_p)$ une base (non nécessairement orthonormée) de . Montrer que la distance de au sous-espace vectoriel est donnée par :

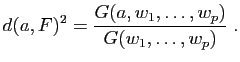
$\displaystyle d(a,F)^2=\frac{G(a,w_1,\ldots ,w_p)}{G(w_1,\ldots ,w_p)}\; .$

4) On suppose orienté de dimension 3. Montrer que $G(v_1,v_2)=\Vert v_1 \wedge v_{2}\Vert^2$ pour tout couple de vecteurs de .

5) Soient trois vecteurs unitaires de et $\alpha,\beta,\gamma$ trois éléments de $\,[0,\pi]\,$ tels que

$\displaystyle \la u_1,u_2 \ra=\cos\alpha,\quad \la u_2,u_3 \ra=\cos\beta,\quad \la u_3,u_1 \ra=\cos\gamma\; .$

Calculer et en déduire les inégalités

$\displaystyle \alpha+\beta+\gamma\leq 2\pi,\quad \alpha\leq \beta+\gamma,\quad \beta\leq \gamma+\alpha, \quad \gamma\leq \alpha+\beta \; .$

Interpréter géométriquement ces inégalités.

Exercice 17 Soit un espace vectoriel euclidien de dimension , $(v_1,\dots,v_n)$ une base de , la matrice de Gram de la famille $(v_1,\dots,v_n)$ , un endomorphisme de de matrice dans la base $(v_1,\dots,v_n)$ .

1) Exprimer en fonction de et de la matrice de l'endomorphisme adjoint de dans la base $(v_1,\dots,v_n)$ .

2) Montrer que est symétrique si et seulement si $GA=\tr{A}G$ .

Exercice 18 Quotient de Rayleigh

Soit une matrice symétrique réelle d'ordre . On définit, pour tout vecteur colonne non nul $X\in\mathbb{R}^n$ , le quotient de Rayleigh par

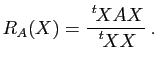
$\displaystyle R_A(X)=\dfrac{\tr{X}AX}{\tr{X}X} \; .$

1) Montrer que $R_A(\lambda X)=R_A(X)$ pour tout réel $\lambda$ non nul.

2) Montrer que la plus grande (resp. la plus petite) valeur propre $\lambda_{\min}$ (resp. $\lambda_{\max}$ ) de est donnée par

	$\displaystyle \lambda_{\max}=\max_{X\in\mathbb{R}^n,\; X\not=0}R_A(X)=\max_{X\in\mathbb{R}^n,\; \Vert X\Vert=1}R_A(X)$
	$\displaystyle \lambda_{\min}=\min_{X\in\mathbb{R}^n,\; X\not=0}R_A(X)=\min_{X\in\mathbb{R}^n,\; \Vert X\Vert=1}R_A(X) \; .$

Exercice 19 1) Montrer que toute matrice symétrique positive (i.e. vérifiant $^t\! X \, A\, X \geq 0$ pour tout ) possède une racine carrée symétrique positive (i.e. une matrice symétrique positive vérifiant ).

2) En déduire que toute matrice symétrique positive d'ordre est la matrice de Gram d'une famille de vecteurs.

Exercice 20 Inégalité de Hadamard

Soit $(v_1,\dots,v_n)$ une famille libre de vecteurs d'un espace vectoriel euclidien de dimension , $(e_1,\dots,e_n)$ une base orthonormale de et $(e'_1,\dots,e'_n)$ la base orthonormale de obtenue à partir de $(v_1,\dots,v_n)$ par le procédé d'orthonormalisation de Gram-Schmidt. On note

la matrice de passage de la base $(e_1,\dots,e_n)$ à la base $(v_1,\dots,v_n)$ ;
la matrice de passage de la base $(e_1,\dots,e_n)$ à la base $(e'_1,\dots,e'_n)$ ;
la matrice de passage de la base $(e'_1,\dots,e'_n)$ à la base $(v_1,\dots,v_n)$ .

1) Que peut-on dire des matrices et ?

2) Montrer que .

3) Comparer les matrices $^t\! M M$ et $^t\!T T$ .

4) En déduire une relation entre les normes des vecteurs colonnes de et celles des vecteurs colonnes de .

5) Exprimer la valeur absolue du déterminant de en fonction des coefficients diagonaux $t_{i,i}$ de .

6) En déduire que la valeur absolue du déterminant d'une matrice carrée réelle est inférieure ou égale au produit des normes euclidiennes de ses vecteurs colonnes et que la valeur absolue du déterminant de vecteurs d'un espace vectoriel euclidien orienté de dimension est inférieure ou égale au produit des normes de ces vecteurs. Interpréter ces inégalités en termes d'aire ou de volume quand ou . Dans quels cas a-t-on l'égalité ?

Exercice 21 Soit $A\in M_3(\mathbb{R})$ une matrice symétrique définie positive et l'ellipsoïde plein

$\displaystyle V=\{ (x_1,x_2,x_3)\in \mathbb{R}^3 \mid ^t\!X A X \leq 1\}$

où $X=\, ^t\!(x_1,x_2,x_3)$ . Exprimer en fonction des valeurs propres de le rayon de la plus petite boule de centre l'origine contenant et le rayon de la plus grande boule de centre l'origine contenue dans .

Exercice 22 Méthode des moindres carrés

Soit $A\in {\cal M}_{n,m}(\mathbb{R})$ une matrice réelle à lignes et colonnes et un vecteur de $\mathbb{R}^n$ . On identifiera à l'application linéaire de $\mathbb{R}^m$ dans $\mathbb{R}^n$ qui lui est naturellement associée et à la matrice colonne de ses composantes.

On dit que le vecteur colonne $U\in \mathbb{R}^m$ est solution du problème des moindres carrés associé au couple si

$\displaystyle \Vert AU-V\Vert=\min \{ \Vert AW-V\Vert \mid W\in \mathbb{R}^m\}\, .$

1) Montrer que $U\in \mathbb{R}^m$ est solution du problème des moindres carrés associé au couple si et seulement si est le projeté orthogonal de sur le sous-espace vectoriel $\mathrm{Im}\, A$ de $\mathbb{R}^n$ .

2) En déduire que $U\in \mathbb{R}^m$ est solution du problème des moindres carrés associé au couple si et seulement si est orthogonal à $\mathrm{Im}\, A$ , ou encore si et seulement si $^tAAU \,=\, ^tAV$ .

3) Montrer que si le rang de est , le problème des moindres carrés associé au couple admet une unique solution, et que si le rang de est strictement plus petit que , l'ensemble des solutions est un sous-espace affine de $\mathbb{R}^m$ de dimension rg.

4) On suppose le rang de égal à . Montrer que l'erreur $\delta=\Vert AU-V\Vert$ au sens des moindres carrés du problème associé à (dont $\U$ est l'unique solution) est donnée par :

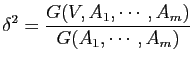
$\displaystyle \delta^2=\dfrac{G(V,A_1,\cdots,A_m)}{G(A_1,\cdots,A_m)}$

où $A_1,\cdots,A_m$ sont les vecteurs colonnes de et le déterminant de Gram.

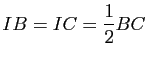Exercice 23 Soient et deux points d'un espace affine euclidien et et deux réels positifs vérifiant . Montrer qu'il existe un et un seul point de vérifiant et et que ce point appartient au segment . En particulier le milieu de est l'unique point de vérifiant $IB=IC=\dfrac{1}{2}BC$ .

Exercice 24 Fonction scalaire de Leibniz

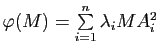Soit $(A_i,\lambda_i)_{i=1,\dots,n}$ un système de points pondérés d'un espace affine euclidien . On définit une fonction $\varphi$ de dans $\mathbb{R}$ par $\varphi(M)=\sum\limits_{i=1}^n \lambda_i MA_i^2$ .

1) On suppose 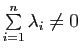$\sum\limits_{i=1}^n \lambda_i \not =0$ . Montrer que 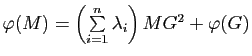$\varphi(M)=\left( \sum\limits_{i=1}^n \lambda_i \right) MG^2+\varphi(G)$ , où est le barycentre du système pondéré $(A_i,\lambda_i)_{i=1,\dots,n}$ .
En particulier, si est le milieu d'un segment , on obtient l'identité de la médiane :

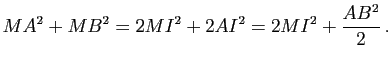
$\displaystyle MA^2+MB^2=2 MI^2+2 AI^2=2 MI^2+\dfrac{AB^2}{2}\, .$

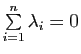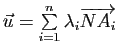2) On suppose $\sum\limits_{i=1}^n \lambda_i =0$ . Montrer que $\varphi(M)=2\vv{MN}\cdot \u +\varphi(N)$ pour tout couple de points de , où le vecteur $\u=\sum\limits_{i=1}^n \lambda_i \vv{NA_i}$ ne dépend pas du point .

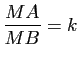3) Application : Soient et deux points d'un plan affine euclidien et un réel non nul. Déterminer l'ensemble des points de vérifiant (resp. , $\dfrac{MA}{MB}=k$ ).

Exercice 25 Le plan est rapporté à un repère orthonormé . Donner l'expression en coordonnées de la projection orthogonale sur la droite d'équation , puis de la symétrie orthogonale par rapport à cette même droite.

Exercice 26 Théorème des trois perpendiculaires

Soit un plan de l'espace affine euclidien de dimension et une droite incluse dans ce plan. On note (resp. ) la projection orthogonale sur (resp. ). Montrer que $p_D=p_D\circ p_P$ . Si est un point de , son projeté orthogonal sur et son projeté orthogonal sur , écrire une relation entre , et .

Exercice 27 L'espace est rapporté à un repère orthonormé. Donner des équations de la perpendiculaire commune aux droites d'équations

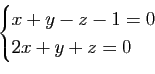
$\begin{displaymath}\begin{cases} x+y-z-1=0\\ 2x+y+z=0 \end{cases}\end{displaymath}$

et déterminée par le point de coordonnées et le vecteur directeur $\v_2$ de composantes . Calculer la distance de ces deux droites.

Exercice 28 Montrer qu'un point d'un espace affine euclidien est uniquement déterminé par ses distances aux points d'un repère affine, i.e. que si $(A_0,A_1,\dots,A_n)$ est un repère affine de , l'application $M \mapsto (MA_0, MA_1,\dots,MA_n)$ de dans $\mathbb{R}^{n+1}$ est injective.

Exercice 29 Soit un espace affine euclidien et la projection affine sur un sous-espace affine de dans la direction d'un sous-espace affine . Montrer que est 1-lipschitzienne (i.e. vérifie $p(M)p(N)\leq MN$ pour tout couple de points de ) si et seulement si est une projection orthogonale (i.e. si et seulement si et sont des sous-espaces vectoriels supplémentaires orthogonaux de ).

Exercice 30 L'espace affine euclidien de dimension 3 est rapporté à un repère orthonormé. Donner une condition nécessaire et suffisante pour que deux plans et d'équations respectives et soient perpendiculaires.

Exercice 31 Montrer que deux droites orthogonales de l'espace affine euclidien de dimension 3 se projettent orthogonalement sur un plan en deux droites orthogonales si et seulement si l'une de ces droites est parallèle à , l'autre n'étant pas orthogonale à .

Exercice 32 Soit, dans l'espace rapporté à un repère orthonormé, la droite d'équations

$\displaystyle x+4y+z-12=0,\quad 2x+2y-z-9=0$

et la droite définie par le point de coordonnées et le vecteur directeur $\v_2$ de composantes .

1) Donner un vecteur directeur de .

2) Donner un vecteur directeur de la perpendiculaire commune $\Delta$ à et .

3) Donner une équation cartésienne du plan défini par et $\Delta$ .

4) Donner une équation cartésienne du plan défini par et $\Delta$ .

5) Donner les coordonnées des pieds de la perpendiculaire commune $\Delta$ .

6) Calculer la distance de la droite à la droite .

Exercice 33 Dans l'espace affine euclidien de dimension rapporté à un repère orthonormé d'origine , on considère les trois points , , , avec $abc\not =0$ .

1) Ecrire l'équation du plan . Donner un vecteur normal à ce plan.

2) Montrer que le projeté orthogonal de sur le plan est l'orthocentre du triangle .

3) Ecrire l'équation de la sphère circonscrite au tétraèdre . Déterminer son rayon et les coordonnées de son centre $\Omega$ . Comparer les vecteurs $\vv{O\Omega}$ et $\vv{OG}$ , où est l'isobarycentre des sommets du tétraèdre.

Exercice 34 Soit un tétraèdre non aplati de l'espace affine euclidien de dimension 3. Montrer qu'il existe une sphère et une seule passant par les 4 points , , et . Cette sphère est appelée sphère circonscrite au tétraèdre.

Exercice 35 Dans l'espace rapporté à un repère orthonormé, on considère les deux sphères et d'équations respectives :

$\displaystyle x^2+y^2+z^2-2x+4y-6z-11=0$

$\displaystyle x^2+y^2+z^2-6x-4z+9=0\; .$

1) Donner pour chacune de ces sphères les coordonnées de son centre et son rayon.

2) Montrer que et sont tangentes. Donner les coordonnées de leur point de contact et l'équation de leur plan tangent en ce point.

3) Montrer qu'il existe exactement deux homothéties transformant en . Donner pour chacune de ces homothéties son rapport et les coordonnées de son centre.

Exercice 36 Soient, dans le plan affine euclidien rapporté à un repère orthonormé $(O,\vi,\vj)$ , et deux droites sécantes d'équations respectives et . Ecrire l'équation de la réunion des deux bissectrices de ces droites.

Exercice 37 Soient et deux plans de l'espace affine euclidien de dimension d'équations respectives et dans un repère orthonormé. Déterminer l'ensemble des points de équidistants de et .

Exercice 38 Montrer que, dans le plan affine euclidien rapporté à un repère orthonormé, la tangente en au cercle d'équation a pour équation .

Exercice 39 Montrer que par tout point du plan extérieur à un cercle de centre on peut mener deux tangentes à et que ces tangentes sont symétriques par rapport à la droite . Donner une construction de ces tangentes.

Exercice 40 Ecrire l'équation de l'axe radical de deux cercles donnés par leurs équations cartésiennes en repère orthonormé et . Vérifier que cet axe radical est perpendiculaire à la droite des centres.

Exercice 41 On suppose les cercles et sécants en et . Montrer que le faisceau de cercles engendré par et est exactement l'ensemble des cercles du plan passant par et .

Exercice 42 On suppose les cercles et tangents en un point . Montrer que le faisceau de cercles engendré par et est exactement l'ensemble des cercles du plan tangents en à et .

Exercice 43 Cercles orthogonaux

Soient, dans le plan affine euclidien, et deux cercles de centres respectifs et et de rayons respectifs et . Montrer l'équivalence des propriétés suivantes :

(i): les cercles et sont sécants et leurs tangentes en leurs points d'intersection sont orthogonales ;
(ii): ;
(iii): $p_{C}(O')=R'^2$ ;
(iv): $p_{C'}(O)=R^2$ .

Deux cercles et remplissant ces conditions sont dits orthogonaux.

Exercice 44 Faisceaux de cercles orthogonaux

1) Montrer qu'un cercle orthogonal à deux cercles d'un faisceau est orthogonal à tout cercle du faisceau.

2) En déduire que l'ensemble des cercles orthogonaux à tous les cercles d'un faisceau est un autre faisceau de cercles, et que l'axe radical de l'un ces faisceaux est la droite des centres de l'autre.

Exercice 45 Arc capable.

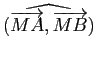Soient et deux points distincts du plan affine euclidien orienté et $\alpha$ un réel. Déterminer l'ensemble des points du plan tels que la mesure de l'angle orienté de vecteurs $\widehat{(\vv{MA},\vv{MB})}$ soit congrue à $\alpha$ modulo $\pi$ (resp. modulo $2\pi$ ). En déduire l'ensemble des points du plan tels que la mesure de l'angle géométrique $\wh{AMB}$ soit égale à $\alpha$ .

Exercice 46 Soient , , trois réels positifs. Montrer qu'il existe un triangle de longueurs de côtés , , si et seulement si on a la double inégalité : $\vert b-c\vert<a<b+c$ .

Exercice 47 Montrer qu'un triangle est isocèle en si et seulement si les angles géométriques $\hat B$ et $\hat C$ sont égaux. Un triangle est donc équilatéral si et seulement si ses trois angles sont égaux.

Exercice 48 1) Montrer que, pour tout quadruplet de points d'un espace affine euclidien , on a :

$\displaystyle \vv{MA}\cdot \vv{BC}+\vv{MB}\cdot \vv{CA}+\vv{MC}\cdot \vv{AB}=0\; .$

2) Redémontrer en utilisant cette relation que les hauteurs d'un triangle sont concourantes.

3) Montrer que si deux des trois couples d'arêtes opposées d'un tétraèdre sont constitués de droites orthogonales, le troisième couple l'est aussi.

Exercice 49 Tétraèdres orthocentriques

1) Soit, dans l'espace affine euclidien de dimension 3, un tétraèdre non aplati et , , , les projetés orthogonaux des sommets , , , sur les faces opposées (les droites , , , sont appelées hauteurs du tétraèdre).

Démontrer l'équivalence des deux propriétés :

(i): les droites et sont orthogonales ;
(ii): les droites et sont sécantes.

2) Montrer que les quatre hauteurs d'un tétraèdre sont concourantes si et seulement si toute arête de ce tétraèdre est orthogonale à l'arête opposée. Un tel tétraèdre est dit orthocentrique.

3) Montrer qu'un tétraèdre régulier est orthocentrique. Donner un exemple de tétraèdre orthocentrique qui n'est pas régulier.

Exercice 50 Cercle d'Euler

Soit dans le plan affine euclidien un triangle non aplati, son centre de gravité, son orthocentre, , , les milieux des côtés , et , $\Gamma$ le cercle circonscrit au triangle et son centre.

$\includegraphics[width=0.6\textwidth]{euler}$

1) Montrer que l'homothétie $h_{G,-1/2}$ de centre et de rapport transforme le triangle en le triangle .

2) Montrer que les points , et sont alignés. Écrire une relation entre les vecteurs $\overrightarrow{GH}$ et $\overrightarrow{GO}$ .

3) Soit $\Gamma '$ le cercle circonscrit au triangle et son centre. Montrer que $\Gamma '$ est l'image de $\Gamma$ par l'homothétie $h_{G,-1/2}$ , puis que est le milieu de . En déduire que l'homothétie de centre et de rapport transforme $\Gamma$ en $\Gamma '$ , puis que $\Gamma '$ passe par les milieux , et des segments , et .

4) Comparer les vecteurs $\overrightarrow{C'B'}$ et $\overrightarrow{B''C''}$ , puis les vecteurs $\overrightarrow{C'B''}$ et $\overrightarrow{B'C''}$ . Montrer que est un rectangle. En déduire que et sont des diamètres du cercle $\Gamma '$ .

5) Montrer que le cercle $\Gamma '$ passe par les pieds des hauteurs du triangle .

Exercice 51 Montrer que si un quadrilatère convexe possède un cercle inscrit, il vérifie .

$\includegraphics[width=6cm]{quad}$

Exercice 52 Cercle exinscrit et périmètre (théorème des trois tangentes)

$\includegraphics[width=0.8\textwidth]{troistangentes}$

Soit un triangle, , , les points de contact du cercle exinscrit dans l'angle en avec les côtés , et . Montrer que la somme est égale au périmètre du triangle . En déduire le théorème des trois tangentes : soit un point extérieur à un cercle $\Gamma$ , et les deux tangentes menées de à $\Gamma$ , un point de l'arc $\overset{\frown}{QR}$ du cercle $\Gamma$ situé du côté de , et les points d'intersection de la tangente en à $\Gamma$ avec les droites et ; alors le périmètre du triangle ne dépend pas de .

Exercice 53 Droites de Simson et de Steiner

Soit un triangle du plan affine euclidien. Montrer qu'un point du plan appartient au cercle circonscrit à si et seulement si ses projetés orthogonaux sur les trois côtés (resp. ses symétriques par rapport aux trois côtés) sont alignés. La droite qui les porte s'appelle la droite de Simson (resp. la droite de Steiner) de ce point.

$\includegraphics[width=0.8\textwidth]{simson}$

Exercice 54 Soit un triangle et , , trois points situés respectivement sur les côtés , et de ce triangle et différents des sommets. Montrer que les cercles circonscrits aux trois triangles , et ont un point commun.

$\includegraphics[width=0.8\textwidth]{pivot}$

Exercice 55 Montrer qu'un déplacement du plan qui admet deux points fixes distincts est l'identité. Que peut-on dire d'un antidéplacement du plan qui admet deux points fixes distincts ? d'une isométrie plane qui admet deux points fixes distincts ?

Exercice 56 Soit et deux couples de points distincts du plan affine euclidien vérifiant . Montrer qu'il existe un et seul déplacement (resp. un et un seul antidéplacement ) du plan vérifiant et (resp. et ). Construire géométriquement les éléments caractéristiques de et de .

Exercice 57 Soient et deux cercles du plan de centres et distincts et de rayons et distincts.

1) Montrer qu'il existe exactement deux homothéties transformant en . Indiquer une construction des centres de ces homothéties.

2) Déterminer l'ensemble des centres des similitudes directes transformant en .

Exercice 58 Soit un triangle, le rayon de son cercle circonscrit, son aire. On note le pied de la hauteur issue de et le point diamétralement opposé à sur le cercle circonscrit à .

1) Montrer que les triangles et sont semblables.

2) En déduire la relation $AB\times BC\times CA=4 \, R\, S$ .

Exercice 59 Hauteurs et triangle orthique

Soit un triangle non aplati du plan affine euclidien et , , les pieds des hauteurs.

1) Montrer que les côtés du triangle sont des bissectrices du triangle . On suppose que le triangle a tous ses angles aigus. Montrer que les hauteurs , et du triangle sont les bissectrices intérieures du triangle .

2) Soient , , trois points distincts situés respectivement sur les côtés , et du triangle et tels que les côtés du triangle soient des bissectrices du triangle et $f=s_{AB}\circ s_{CA}\circ s_{BC}$ la composée des réflexions d'axes ces côtés. Montrer que est une symétrie glissée laissant globalement invariante la droite . En déduire que cette droite est l'axe de la symétrie glissée , puis que les points , , sont les pieds des hauteurs du triangle .

Exercice 60 Soit une droite du plan affine euclidien et et deux points du plan situés d'un même côté de cette droite. Déterminer le point de la droite qui minimise la somme .

Exercice 61 Problème de Fagnano

Soit un triangle du plan affine euclidien dont tous les angles sont aigus. On cherche à déterminer un triangle de périmètre minimal inscrit dans le triangle , c'est-à-dire un triangle dont les sommets , et appartiennent respectivement aux côtés , et du triangle et tel que la somme soit minimale.

1) Montrer en utilisant l'exercice précédent que si , et sont trois points intérieurs aux côtés du triangle tels que le triangle soit solution de ce problème, alors les côtés du triangle sont les bissectrices extérieures du triangle . En déduire que les points , , sont les pieds des hauteurs du triangle .

2) Soit le pied de la hauteur issue de dans le triangle , et les symétriques de par rapport à et . Montrer que les points , , et sont alignés et que le périmètre du triangle est égal à . Exprimer ce périmètre en fonction de et de l'angle en du triangle . En déduire que le problème de minimisation admet une solution unique donnée par les pieds des hauteurs.

$\includegraphics[width=0.6\textwidth]{fagnano}$

Exercice 62 Isométries du rectangle et du losange

Déterminer le groupe des isométries planes conservant :

un carré ;
un rectangle qui n'est pas un carré ;
un losange qui n'est pas un carré ;
un parallélogramme qui n'est ni un rectangle ni un losange.

Exercice 63 L'espace affine euclidien de dimension 3 est rapporté à un repère orthonormé. Déterminer la nature géométrique de la transformation de qui à un point de coordonnées associe le point de coordonnées définies par :

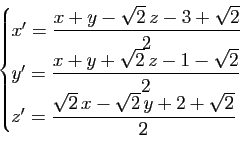
$\begin{displaymath}\begin{cases} x'=\dfrac{x+y-\sqrt{2} \, z-3+\sqrt{2}}{2}\\ y... ... z'=\dfrac{\sqrt{2}\, x-\sqrt{2}\, y+2+\sqrt{2}}{2} \end{cases}\end{displaymath}$

(on précisera les éléments caractéristiques de cette transformation).

Exercice 64 L'espace affine euclidien de dimension 3 est rapporté à un repère orthonormé. Déterminer la nature géométrique de la transformation de qui à un point de coordonnées associe le point de coordonnées définies par :

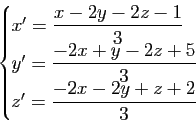
$\begin{displaymath}\begin{cases} x'=\dfrac{x-2y-2z-1}{3}\\ y'=\dfrac{-2x+y-2z+5}{3}\\ z'=\dfrac{-2x-2y+z+2}{3} \end{cases}\end{displaymath}$

(on précisera les éléments caractéristiques de cette transformation).

Exercice 65 Soit un espace affine euclidien de dimension 3, $(O,\vec i, \vec j ,\vec k)$ un repère orthonormé de , , , les points de définis par $\vv{OA}=\vec i$ , $\vv{OB}=\vec j$ , $\vv{OC}=\vec k$ . Déterminer le groupe des isométries de laissant globalement invariant l'ensemble $\{O, A, B, C\}$ . Préciser la nature géométrique des éléments de et écrire les matrices de leurs parties linéaires dans la base $(\vec i, \vec j , \vec k)$ de $\vv{E}$ . Montrer que est isomorphe au groupe des permutations de trois éléments.

Exercice 66 Soit un espace affine euclidien de dimension 3, $\vec i$ , $\vec j$ , $\vec k$ une base orthonormée de l'espace vectoriel $\vec E$ associé, et deux points de vérifiant $\overrightarrow{AB}=\vec k$ . On note la droite de vecteur directeur $\vec i$ passant par , la droite de vecteur directeur $\vec j$ passant par , et, pour , le retournement d'axe .

1) Écrire les matrices des parties linéaires de , , $s_2 \circ s_1$ et $s_1\circ s_2$ dans la base $(\vec i, \vec j , \vec k)$ .

2) Montrer que $f=s_2 \circ s_1$ est un vissage dont on précisera l'axe et le vecteur.

3) Calculer . Déterminer les images et de et par .

4) Soit le sous-groupe du groupe des isométries de engendré par et . Montrer qu'il existe une droite de globalement invariante par tout élément de .

5) Décrire géométriquement tous les éléments de .

Exercice 67 Isométries du cube, du tétraèdre et de l'octaèdre

Soit un cube de diagonales , , , dont le carré est une face. On se propose de déterminer le groupe des isométries de l'espace conservant ce cube et de comparer ce groupe aux groupes des isométries du tétraèdre et de l'octaèdre.

1) Montrer que tout élément de transforme toute diagonale du cube en une diagonale du cube. En déduire que tout élément de laisse globalement invariant l'ensemble des sommets du cube. Réciproquement, montrer que toute isométrie de l'espace laissant globalement invariant l'ensemble des sommets du cube conserve le cube.

$\includegraphics[width=0.45\textwidth]{tetraedres}$ $\includegraphics[width=0.45\textwidth]{octaedre}$

2) Soit $\varphi$ l'application de dans l'ensemble $\mathcal S$ des permutations des diagonales du cube qui à tout élément de associe la permutation induite sur l'ensemble des diagonales. Montrer que $\varphi$ est un morphisme de groupes et que sa restriction au sous-groupe des isométries directes de est injective.

3) Identifier les éléments de et montrer que $\varphi$ est un isomorphisme de sur $\mathcal S$ .

4) En considérant la symétrie centrale de centre le centre du cube, montrer que est isomorphe au produit direct de $\mathcal S$ par un groupe à 2 élements.

5) Soit et les deux tétraèdres réguliers dont les arêtes sont les diagonales des faces du cube. Montrer que l'ensemble des éléments de qui conservent est un sous-groupe de , et que est réunion disjointe de et de l'ensemble des éléments de qui échangent et . Retrouver ainsi la structure de (on rappelle que le groupe des isométries du tétraèdre régulier est isomorphe au groupe des permutations de 4 éléments).

6) Montrer que les ensembles des milieux des arêtes de et de sont les mêmes (ces milieux sont aussi les centres de gravité des faces du cube) et que ces milieux constituent les sommets d'un octaèdre régulier. Montrer que tout élément de conserve cet octaèdre. En déduire une injection naturelle du groupe du tétraèdre dans celui de l'octaèdre.

7) Montrer que les groupes des isométries du cube et de l'octaèdre sont isomorphes.

Exercice 68 Isométries de l'hélice circulaire

Soit, dans l'espace affine euclidien de dimension 3 rapporté à un repère orthonormé $(O,\vec i, \vec j ,\vec k)$ , l'hélice circulaire de représentation paramétrique $x=R \cos t, \; y= R \sin t, \; z=at$ , $t\in \mathbb{R}$ , où et sont deux réels strictement positifs donnés.

1) Montrer que toute isométrie de $\mathbb{R}$ est de la forme $t\longmapsto t+b$ ou $t\longmapsto 2b-t$ pour un certain réel .

2) Montrer que pour toute isométrie $\varphi$ de $\mathbb{R}$ , il existe un et un seul déplacement de qui transforme, pour tout $t\in \mathbb{R}$ , le point de paramètre de en le point de paramètre $\varphi(t)$ de . Un tel déplacement conserve donc l'hélice. Expliciter la nature géométrique de ce déplacement (on discutera suivant la valeur de $\varphi$ ).

3) Montrer que toute isométrie conservant l'hélice conserve l'axe du repère. En déduire que les déplacements décrits à la question précédente sont les seuls à conserver et que le groupe des déplacements de l'hélice est donc isomorphe au groupe des déplacements de la droite.

4) Montrer qu'il n'existe pas d'antidéplacement de qui conserve .

Exercice 69 Montrer qu'une application du plan complexe dans lui-même est affine si et seulement si elle est de la forme $f(z)=az+b\bar z+c$ pour 3 nombres complexes , et . Donner l'expression complexe de , ainsi qu'une condition nécessaire et suffisante portant sur et pour que soit bijective.

Exercice 70 Montrer que tout cercle du plan complexe est défini par une équation de la forme $z\bar z-a \bar z -\bar a z+c=0$ , où est un nombre complexe et un réel vérifiant $c-\vert a\vert^2<0$ . Montrer que réciproquement toute équation de ce type est celle d'un cercle.

Exercice 71 Soient et deux nombres complexes non nuls. Donner une condition nécessaire et suffisante pour que $\vert a+b\vert=\vert a\vert+\vert b\vert$ . Interpréter géométriquement cette condition.

Exercice 72 Soient , , trois points du plan complexe d'affixes respectives , , .

1) Donner une condition nécessaire et suffisante sur , , pour que l'origine soit le centre du cercle circonscrit au triangle .

2) Donner une condition nécessaire et suffisante sur , , pour que l'origine soit le centre de gravité du triangle .

3) Donner une condition nécessaire et suffisante pour que la somme de trois nombres complexes non nuls de même module soit nulle.

Exercice 73 Soient et les deux applications de $\mathbb{C}$ dans $\mathbb{C}$ définies par , . Donner la nature géométrique de , et $g\circ f$ (on précisera les éléments caractéristiques de chacune de ces transformations).

Exercice 74 Déterminer la nature géométrique et les éléments caractéristiques des applications et de $\mathbb{C}$ dans $\mathbb{C}$ définies par $f(z)=2j\bar{z}+j^2$ et $g(z)= j \bar{z}+j^2$ , où $j=e^{\frac{2i\pi}{3}}$ .

Exercice 75 Soient , , , quatre points distincts du plan d'affixes respectives , , , .

1) Montrer l'équivalence de :

(i): l'unique similitude directe transformant en et en admet un point fixe ;
(ii): l'unique similitude directe transformant en et en admet un point fixe.

2) On suppose cette condition remplie. Donner les expressions complexes de et de . Montrer que et ont même centre.

3) Retrouver géométriquement ce résultat.

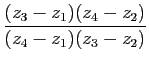Exercice 76 Montrer quatre points distincts d'affixes respectives , , , sont alignés ou cocycliques si et seulement si leur birapport $\dfrac{(z_3-z_1)(z_4-z_2)}{(z_4-z_1)(z_3-z_2)}$ est réel.

Exercice 77 Théorème de Ptolémée

Soient , , , quatre points du plan complexe, d'affixes respectives , , et .

1) Montrer qu'on a toujours l'inégalité :

$\displaystyle AC . BD \leq AB . CD+AD . BC \quad \quad (*)$

(le produit des longueurs des diagonales d'un quadrilatère est inférieur à la somme des produits des longueurs des côtés opposés).

2) Montrer qu'on a égalité dans si et seulement si les quatre points , , , sont cocycliques ou alignés dans cet ordre.

Exercice 78 Montrer que toute application linéaire non nulle d'un espace vectoriel euclidien dans lui-même qui préserve l'orthogonalité est une similitude.

Exercice 79 Donner une condition nécessaire et suffisante sur les affixes , , de trois points , , du plan complexe pour que le triangle soit équilatéral.

Exercice 80 On construit à l'extérieur d'un parallélogramme quatre carrés de bases les côtés et de centres , , , .

$\includegraphics[width=6cm]{carres}$

1) Calculer les affixes des points , , , en fonction des affixes de , , , .

2) En déduire que est un carré.

Exercice 81 À l'extérieur d'un triangle , on construit trois carrés de bases les côtés et de centres , , . Montrer que les segments et (resp. et , et ) sont orthogonaux et de même longueur. En déduire que les droites , et sont concourantes.

$\includegraphics[width=8cm]{vecten}$