-
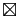 Deux vecteurs
Deux vecteurs  et
et  sont orthogonaux si et seulement si
sont orthogonaux si et seulement si
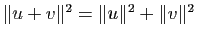 .
.
-
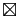 Deux vecteurs
Deux vecteurs  et
et  sont orthogonaux si et seulement si
sont orthogonaux si et seulement si
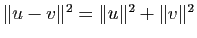 .
.
 Deux vecteurs
Deux vecteurs  et
et  ont même norme si et seulement si les vecteurs
ont même norme si et seulement si les vecteurs 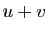 et
et 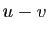 ont même norme.
ont même norme.
-
 Deux vecteurs
Deux vecteurs  et
et  ont même norme si et seulement si les vecteurs
ont même norme si et seulement si les vecteurs 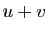 et
et 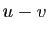 sont orthogonaux.
sont orthogonaux.
-
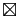 Deux vecteurs
Deux vecteurs  et
et  sont orthogonaux si et seulement si les vecteurs
sont orthogonaux si et seulement si les vecteurs 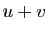 et
et 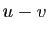 ont même norme.
ont même norme.
-
 Soient
Soient  et
et 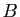 deux parties de
deux parties de  telles que
telles que
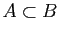 . Alors
. Alors
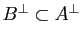 .
.
 Soient
Soient  et
et 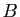 deux parties non vides de
deux parties non vides de  telles que
telles que
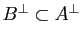 . Alors
. Alors
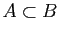 .
.
-
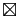 Soient
Soient  et
et 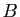 deux parties non vides de
deux parties non vides de  telles que
telles que
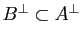 . Alors
. Alors
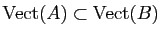 .
.
 Soient
Soient  et
et 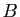 deux parties non vides de
deux parties non vides de  telles que
telles que
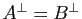 . Alors
. Alors 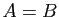 .
.
-
 Soient
Soient  et
et  deux sous-espaces vectoriels de
deux sous-espaces vectoriels de  tels que
tels que
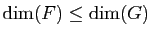 . Alors
. Alors
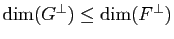 .
.
-
 Soient
Soient  et
et  deux sous-espaces vectoriels de
deux sous-espaces vectoriels de  . Alors
. Alors
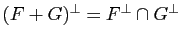 .
.
-
 Soient
Soient 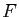 et
et  deux sous-espaces vectoriels de
deux sous-espaces vectoriels de  . Alors
. Alors
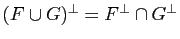 .
.
 Soient
Soient 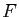 et
et  deux sous-espaces vectoriels de
deux sous-espaces vectoriels de  . Alors
. Alors
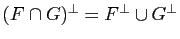 .
.
 Soient
Soient 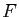 et
et  deux sous-espaces vectoriels de
deux sous-espaces vectoriels de  . Alors
. Alors
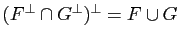 .
.
-
 Soient
Soient 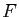 et
et  deux sous-espaces vectoriels de
deux sous-espaces vectoriels de  . Alors
. Alors
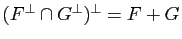 .
.
-
 Soient
Soient 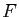 et
et  deux sous-espaces vectoriels supplémentaires de
deux sous-espaces vectoriels supplémentaires de  . Alors
. Alors 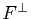 et
et 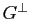 sont des sous-espaces vectoriels supplémentaires de
sont des sous-espaces vectoriels supplémentaires de  .
.
 Soient
Soient 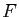 et
et  deux sous-espaces vectoriels de
deux sous-espaces vectoriels de  tels que
tels que 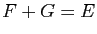 . Alors
. Alors
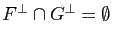 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales