Le groupe affine

Définition 21 Soit un espace affine. On appelle transformation affine de toute application affine bijective de dans lui-même. Les transformations affines de constituent un sous-groupe (pour la composition) du groupe des permutations de . Le groupe des transformations affines de est appelé groupe affine de , et noté .

Proposition 27 L'application $f \longmapsto \vec{f}$ est un homomorphisme surjectif du groupe affine dans le groupe linéaire $GL(\overrightarrow{E})$ (groupe des applications linéaires bijectives de $\overrightarrow{E}$ dans lui-même). Son noyau est le sous-groupe des translations de .

Il en résulte que le groupe des translations de

est un sous-groupe distingué de

Démonstration : La première assertion résulte de la relation 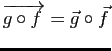$\overrightarrow{g\circ f }=\vec{g}\circ \vec{f}$ pour tout couple d'éléments de

et du fait que pour tout $\vec{f}\in GL(\overrightarrow{E})$ et tout couple

de points de

, il existe une transformation affine $f\in GA(E)$ et une seule de partie linéaire $\vec{f}$ vérifiant

. La seconde vient de ce qu'un élément

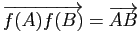est une translation si et seulement si sa partie linéaire $\vec{f}$ est l'identité de $\overrightarrow{E}$ . En effet la relation $\overrightarrow{f(A)f(B)}=\overrightarrow{AB}$ équivaut à la relation 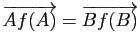$\overrightarrow{Af(A)}=\overrightarrow{Bf(B)}$ (le quadrilatère

est alors un parallélogramme). Elle est donc vraie pour tout couple

de points de

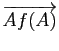si et seulement si le vecteur $\overrightarrow{Af(A)}$ ne dépend pas du point

. $\square$

Le groupe affine

opère sur

par l'application $(f,M)\longmapsto f(M)$ . Rappelons qu'on appelle alors stabilisateur d'un point

le sous-groupe $\Stab (O)$ de

constitué des transformations affines

laissant fixe le point

Proposition 28 Pour tout point de , la restriction de l'application $f \longmapsto \vec{f}$ à $\Stab (O)$ est un isomorphisme de $\Stab (O)$ sur le groupe linéaire $GL(\overrightarrow{E})$ .

Démonstration : L'application $f \longmapsto \vec{f}$ est un morphisme de groupes de

sur $GL(\overrightarrow{E})$ de noyau le groupe des translations de

(proposition 27). Sa restriction à $\Stab (O)$ est injective car une translation ayant un point fixe est l'identité et elle est surjective (pour tout $\vec{f}$ in

, l'application

dans

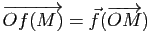définie par $\overrightarrow{Of(M)}=\vec{f}(\overrightarrow{OM})$ est l'unique élément de $\Stab (O)$ de partie linéaire $\vec{f}$ ). $\square$

Proposition 29 L'ensemble $\Fix (f)$ des points fixes d'une transformation affine de est, soit vide, soit un sous-espace affine de direction $\ker (\vec{f}-id_{\overrightarrow{E}})$ (c'est-à-dire le sous-espace propre de $\vec{f}$ associé à la valeur propre 1).

Démonstration : Soit

une origine dans

. Un point

est fixe par

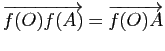si et seulement si $\overrightarrow{f(O)f(A)}=\overrightarrow{f(O)A}$ , i.e. si et seulement si 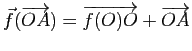$\vec{f}(\overrightarrow{OA})=\overrightarrow{f(O)O}+\overrightarrow{OA}$ , soit encore 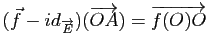$(\vec{f}-id_{\overrightarrow{E}})(\overrightarrow{OA})=\overrightarrow{f(O)O}$ . Si le vecteur 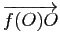$\overrightarrow{f(O)O}$ n'appartient pas à l'image de $\vec{f}-id_{\overrightarrow{E}}$ ,

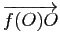n'admet pas de point fixe. Si $\overrightarrow{f(O)O}$ appartient à l'image de $\vec{f}-id_{\overrightarrow{E}}$ , il existe un point

fixe par

. Un point

est alors fixe par

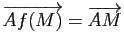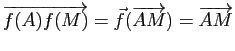si et seulement si $\overrightarrow{Af(M)}=\overrightarrow{AM}$ , i.e. $\overrightarrow{f(A)f(M)}=\vec{f}(\overrightarrow{AM})=\overrightarrow{AM}$ . L'ensemble des points fixes de

est alors le sous-espace affine de

passant par

de direction $\ker (\vec{f}-id_{\overrightarrow{E}})$ . $\square$

Proposition 30 Soit une transformation affine d'un espace affine . Les deux propriétés suivantes sont équivalentes :

(i): admet un point fixe et un seul ;
(ii): 1 n'est pas valeur propre de $\vec{f}$ .

Démonstration : L'implication $(i)\Rightarrow (ii)$ résulte immédiatement de la proposition 29. Montrons que si 1 n'est pas valeur propre de $\vec{f}$ , i.e. si $\vec{f}-id_{\overrightarrow{E}}$ est injective, alors

admet un point fixe et un seul. L'application linéaire $\vec{f}-id_{\overrightarrow{E}}$ étant injective et

de dimension finie, elle est bijective et il résulte de la démonstration de la proposition 29 que

admet un point fixe et un seul. $\square$

Toute transformation affine est composée d'une transformation affine ayant un point fixe et d'une translation. Plus précisément, si

est une transformation affine de

un point quelconque de

, $g=t_{\overrightarrow{f(O)O}}\circ f$ laisse

fixe et l'on a $f=t_{\overrightarrow{Of(O)}}\circ g$ . La proposition suivante étudie le cas où il existe une telle décomposition commutative.

Proposition 31 Soit une transformation affine d'un espace affine telle que le noyau et l'image de $\vec{f}-id_{\overrightarrow{E}}$ soient des sous-espaces vectoriels supplémentaires de $\overrightarrow{E}$ . Alors il existe une transformation affine de admettant un point fixe et une translation de telles que $f=t\circ g=g \circ t$ .

Démonstration : Soit

une origine dans

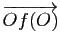. Le vecteur $\overrightarrow{Of(O)}$ se décompose en somme d'un vecteur $\u\in \mathrm{Ker}(\vec{f}-id_{\overrightarrow{E}})$ et d'un vecteur $\v\in\mathrm{Im}(\vec{f}-id_{\overrightarrow{E}})$ . Soit

un point de

tel que $(\vec{f}-id_{\overrightarrow{E}})(\overrightarrow{OA})=-\v$ , i.e. $\vec{f}(\overrightarrow{OA})=\overrightarrow{OA}-\v$ ,

la translation de vecteur $\u$ et $g= t^{-1}\circ f$ . L'égalité :

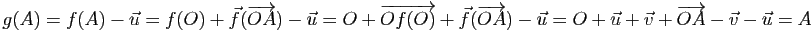
$\displaystyle g(A)=f(A)-\u =f(O)+\vec{f}(\overrightarrow{OA})-\u =O+\overrightarrow{Of(O)}+\vec{f}(\overrightarrow{OA})-\u =O+\u+\v+\overrightarrow{OA}-\v-\u=A$

$\displaystyle f(M+\u)=f(M)+\vec{f}(\u)=f(M)+\u$ pour tout point $M$ de $E$