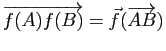 pour tout couple
pour tout couple Les transformations affines sont les transformations géométriques les plus utilisées en géométrie élémentaire. On verra en particulier au chapitre «Géométrie euclidienne» que toute similitude (et en particulier toute isométrie) est une transformation affine. On dira de fait qu'une propriété est affine si elle est conservée par toute transformation affine. En particulier, l'alignement, le parallélisme, le milieu sont des propriétés affines. Par contre l'orthogonalité, les angles, les longueurs ne sont pas des propriétés affines, car elles ne sont pas conservées par toutes les transformations affines (bien qu'elles soient conservées par les isométries).
Définition et premières propriétés
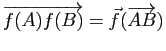 pour tout couple
pour tout couple
Cette propriété peut encore s'écrire
![]() pour tout point
pour tout point ![]() de
de ![]() et tout vecteur
et tout vecteur
![]() .
.
L'application ![]() est alors uniquement déterminée, puisque pour tout vecteur
est alors uniquement déterminée, puisque pour tout vecteur ![]() de
de
![]() , il existe un (en fait une infinité de) couple
, il existe un (en fait une infinité de) couple ![]() de points de
de points de ![]() tel que
tel que
![]() . On l'appelle application linéaire associée à
. On l'appelle application linéaire associée à ![]() , ou partie linéaire de
, ou partie linéaire de ![]() .
.
Une application affine est entièrement déterminée par sa partie linéaire et l'image d'un point, puisque
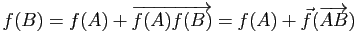 pour tout point
pour tout point ![]() de
de ![]() .
.
Réciproquement, si ![]() et
et ![]() sont deux espaces affines,
sont deux espaces affines, ![]() un point de
un point de ![]() ,
, ![]() un point de
un point de ![]() et
et ![]() une application linéaire de
une application linéaire de
![]() dans
dans
![]() , il existe une (et une seule) application affine
, il existe une (et une seule) application affine ![]() de
de ![]() dans
dans ![]() de partie linéaire
de partie linéaire ![]() vérifiant
vérifiant ![]() .
.
Exemples :
Si ![]() est une application quelconque de
est une application quelconque de ![]() dans
dans ![]() , on ne peut en général pas lui associer d'application de
, on ne peut en général pas lui associer d'application de
![]() dans
dans
![]() indépendamment du choix d'une origine : en effet, on peut bien définir, pour tout point
indépendamment du choix d'une origine : en effet, on peut bien définir, pour tout point ![]() de
de ![]() , une application
, une application ![]() de
de
![]() dans
dans
![]() par
par
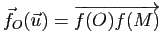 pour tout vecteur
pour tout vecteur ![]() de
de
![]() , où
, où ![]() est l'unique point de
est l'unique point de ![]() tel que
tel que
![]() , mais cette application
, mais cette application ![]() dépend en général du choix de
dépend en général du choix de ![]() . Cependant, il suffit que cette application soit linéaire pour un point
. Cependant, il suffit que cette application soit linéaire pour un point ![]() de
de ![]() pour que
pour que ![]() soit affine comme le montre la proposition suivante :
soit affine comme le montre la proposition suivante :
Démonstration : On a, pour tout couple ![]() de points de
de points de ![]() :
:
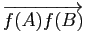 |
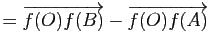 |
|
Composition
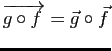 .
.En particulier, on ne change pas la partie linéaire d'une application affine en la composant (à droite ou à gauche) avec une translation.
Démonstration : Il suffit de remarquer que, pour tout couple ![]() de points de l'espace de départ de
de points de l'espace de départ de ![]()
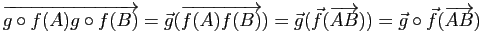
Caractérisation en termes de barycentres
Démonstration : Si ![]() est affine et si
est affine et si ![]() est le barycentre du système
est le barycentre du système
![]() , l'égalité
, l'égalité
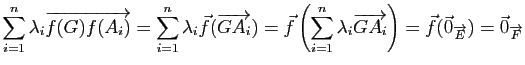
Réciproquement, montrons que si ![]() conserve les barycentres, l'application
conserve les barycentres, l'application ![]() considérée à la proposition 20 est linéaire pour tout point
considérée à la proposition 20 est linéaire pour tout point ![]() de
de ![]() . Soient donc
. Soient donc ![]() et
et ![]() deux vecteurs de
deux vecteurs de
![]() ,
, ![]() et
et ![]() deux réels,
deux réels, ![]() et
et ![]() les points de
les points de ![]() définis par
définis par
![]() ,
,
![]() , et
, et ![]() le point de
le point de ![]() défini par
défini par
![]() . Le point
. Le point ![]() est le barycentre du système pondéré
est le barycentre du système pondéré
![]() . Il en résulte que
. Il en résulte que ![]() est le barycentre du système pondéré
est le barycentre du système pondéré
![]() , d'où
, d'où
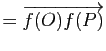 |
||
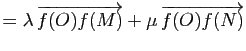 |
||
Démonstration : Il suffit de remarquer que, d'après la proposition précédente, l'image par une application affine ![]() d'un segment
d'un segment ![]() est le segment
est le segment
![]() .
.![]()
Image et image réciproque d'un sous-espace affine
Démonstration : Soit ![]() un sous-espace affine de
un sous-espace affine de ![]() et
et ![]() un point de
un point de ![]() . L'égalité
. L'égalité
![]() implique
implique
Soit ![]() un sous-espace affine de
un sous-espace affine de ![]() . Si
. Si ![]() n'est pas vide, soit
n'est pas vide, soit ![]() un point de
un point de ![]() . Un point
. Un point ![]() de
de ![]() appartient à
appartient à ![]() si et seulement si
si et seulement si ![]() appartient à
appartient à ![]() , i.e. si et seulement si
, i.e. si et seulement si
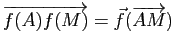 appartient à
appartient à
![]() , ou encore si et seulement si
, ou encore si et seulement si
![]() appartient au sous-espace vectoriel
appartient au sous-espace vectoriel
![]() de
de
![]() , ce qui montre que
, ce qui montre que ![]() est le sous-espace affine de
est le sous-espace affine de ![]() passant par
passant par ![]() et de direction
et de direction
![]() .
.![]()
En particulier :
Démonstration : Une application affine ![]() d'un espace affine
d'un espace affine ![]() dans un espace affine
dans un espace affine ![]() est injective si et seulement si pour tout couple
est injective si et seulement si pour tout couple ![]() de points de
de points de ![]() ,
, ![]() équivaut à
équivaut à ![]() . Mais
. Mais ![]() équivaut à
équivaut à
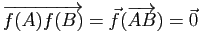 , i.e. à
, i.e. à
![]() et
et ![]() équivaut à
équivaut à
![]() . Il en résulte que
. Il en résulte que ![]() est injective si et seulement si
est injective si et seulement si
![]() , i.e. si et seulement si
, i.e. si et seulement si ![]() est injective.
est injective.
De même ![]() est surjective si et seulement si
est surjective si et seulement si ![]() . Mais
. Mais ![]() est un sous-espace affine de
est un sous-espace affine de ![]() de direction
de direction
![]() ; c'est donc
; c'est donc ![]() si et seulement si
si et seulement si
![]() , i.e. si et seulement si
, i.e. si et seulement si ![]() est surjective.
est surjective.![]()
Expression dans un repère
1) Repère cartésien
Démonstration : Il suffit de remarquer que
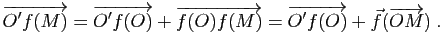
Changement de repère
En appliquant cette formule au cas où ![]() et
et ![]() , on obtient les formules de changement de repère : si
, on obtient les formules de changement de repère : si
![]() et
et
![]() sont deux repères cartésiens de
sont deux repères cartésiens de ![]() , et si
, et si ![]() (resp.
(resp. ![]() ) est le vecteur colonne des coordonnées d'un point
) est le vecteur colonne des coordonnées d'un point ![]() dans le repère
dans le repère
![]() (resp.
(resp.
![]() ), on obtient
), on obtient ![]() , où
, où ![]() est la matrice de passage de la base
est la matrice de passage de la base
![]() à la base
à la base
![]() et
et ![]() le vecteur colonne des coordonnées de l'origine
le vecteur colonne des coordonnées de l'origine ![]() du nouveau repère
du nouveau repère
![]() dans l'ancien repère
dans l'ancien repère
![]() . Il suffit pour le voir d'appliquer la formule précédente en prenant
. Il suffit pour le voir d'appliquer la formule précédente en prenant ![]() , l'espace
, l'espace ![]() étant au départ muni du repère
étant au départ muni du repère
![]() , et à l'arrivée du repère
, et à l'arrivée du repère
![]() . Les vecteurs colonnes de la matrice de passage sont obtenus en exprimant les vecteurs de la nouvelle base
. Les vecteurs colonnes de la matrice de passage sont obtenus en exprimant les vecteurs de la nouvelle base
![]() de
de
![]() dans l'ancienne base
dans l'ancienne base
![]() .
.
Formes affines et hyperplans
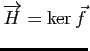 . Plus généralement, toutes les lignes de niveau de
. Plus généralement, toutes les lignes de niveau de 2) Repère affine
Démonstration : L'unicité est évidente : si
![]() sont les coordonnées barycentriques normalisées (
sont les coordonnées barycentriques normalisées (
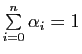 ) du point
) du point ![]() de
de ![]() dans le repère affine
dans le repère affine
![]() , son image par
, son image par ![]() est le point
est le point
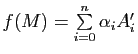 de
de ![]() puisqu'une application affine conserve les barycentres.
puisqu'une application affine conserve les barycentres.
Pour démontrer l'existence, il suffit de vérifier que l'application ![]() de
de ![]() dans
dans ![]() qui à tout point
qui à tout point
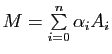 (où
(où
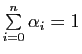 ) associe le point
) associe le point
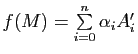 de
de ![]() est affine, et pour cela de vérifier qu'elle conserve les barycentres. Cette propriété résulte de l'associativité du barycentre.
est affine, et pour cela de vérifier qu'elle conserve les barycentres. Cette propriété résulte de l'associativité du barycentre.
L'application ![]() est surjective si et seulement si tout point de
est surjective si et seulement si tout point de ![]() peut s'écrire comme barycentre des points
peut s'écrire comme barycentre des points
![]() et elle est injective si et seulement si cette écriture est unique. Ces deux conditions signifient que
et elle est injective si et seulement si cette écriture est unique. Ces deux conditions signifient que
![]() est un repère affine de
est un repère affine de ![]() .
. ![]()
En particulier deux applications affines qui coïncident sur un repère affine sont égales :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales