Section : Cours
Avant : Repérage
Après : Applications affines

Convexité

Définition

Définition 13   Soient $ A$ et $ B$ deux points d'un espace affine $ E$. Le segment $ AB$, noté $ [AB]$, est l'ensemble des barycentres de $ A$ et $ B$ affectés de coefficients tous deux positifs, i.e. $ [AB]=\{ \alpha A+ (1-\alpha) B\mid \alpha\in[0,1]\}$.

Définition 14   Une partie $ C$ d'un espace affine $ E$ est dite convexe si pour tout couple $ (A,B)$ de points de $ C$ le segment $ [AB]$ est inclus dans $ C$.

Exemples :

Proposition 14   Une partie $ C$ d'un espace affine $ E$ est convexe si et seulement si tout barycentre de points de $ C$ affectés de coefficients tous positifs appartient à $ C$.

Démonstration : Si tout barycentre de points de $ C$ affectés de coefficients tous positifs appartient à $ C$, pour tout couple $ (A,B)$ de points de $ C$ le segment $ [AB]$ est inclus dans $ C$ puisque ce segment est l'ensemble des barycentres de $ A$ et $ B$ affectés de coefficients tous deux positifs. $ C$ est donc convexe.

Réciproquement, si $ C$ est convexe, on démontre par récurrence sur $ n$ que tout barycentre de $ n$ points de $ C$ affectés de coefficients tous positifs appartient à $ C$ : la propriété est vraie pour $ n=2$ par hypothèse ; si elle est vraie pour $ n$ et si $ A_1,\dots,A_{n+1}$ sont $ n+1$ points de $ C$ affectés des coefficients tous positifs $ \alpha_1,\dots,\alpha_{n+1}$, le barycentre $ G$ de ce système de points pondérés est barycentre du système $ [(G',\alpha_1+\dots+\alpha_n),(A_{n+1},\alpha_{n+1})]$ où $ G'$ est le barycentre du système $ (A_i,\alpha_i)_{i=1,\dots,n}$ ; $ G'$ appartient à $ C$ par l'hypothèse de récurrence et $ G$ appartient au segment $ [G'A_{n+1}]$ qui est inclus dans $ C$ car $ C$ est convexe.$ \square$

Proposition 15   Toute intersection de convexes est convexe.

Démonstration : Soit $ \mathcal C$ une famille quelconque de convexes et $ \Gamma=\bigcap\limits_{c\in\mathcal C} C$. Pour tout couple $ (A,B)$ de points de $ \Gamma$ et tout $ C\in \mathcal C$, $ A$ et $ B$ appartiennent à $ C$, donc le segment $ [A,B]$ est inclus dans $ C$. Il en résulte que $ [A,B]$ est inclus dans $ \Gamma$.$ \square$

Remarque : une intersection de convexes peut être vide, mais avec la définition que nous avons choisie l'ensemble vide est convexe.

Enveloppe convexe

Cette stabilité par intersection permet, comme dans le cas des sous-espaces affines, de poser la définition suivante :

Définition 15   Soit $ A$ une partie non vide d'un espace affine $ E$. On appelle enveloppe convexe de $ A$ l'intersection de tous les convexes de $ E$ contenant $ A$.

Proposition 16   L'enveloppe convexe d'une partie non vide $ A$ d'un espace affine $ E$ est le plus petit convexe de $ E$ contenant $ A$. C'est aussi l'ensemble de tous les barycentres de points de $ A$ affectés de coefficients tous positifs.

Démonstration : Soit $ A$ une partie non vide d'un espace affine $ E$ et $ \mathcal C_A$ la famille de tous les convexes de $ E$ contenant $ A$. L'enveloppe convexe $ \Conv (A)=\bigcap\limits_{C\in\mathcal C_A} C$ de $ A$ est convexe comme intersection de convexes et contient $ A$. Tout convexe $ C$ contenant $ A$ appartient à $ \mathcal C_A$ et contient donc $ \Conv (A)$, ce qui montre que $ \Conv (A)$ est le plus petit convexe de $ E$ contenant $ A$.

Soit $ \hat A$ l'ensemble de tous les barycentres de points de $ A$ affectés de coefficients tous positifs. Tout point $ M$ de $ A$ est barycentre de la famille à un élément $ (A,1)$ et appartient donc à $ \hat A$. Par ailleurs, $ \hat A$ est convexe par associativité du barycentre. Il en résulte que $ \Conv (A)$ est inclus dans $ \hat A$.

Soit $ C$ un convexe contenant $ A$. Tout point de $ \hat A$ est barycentre à coefficients tous positifs de points de $ C$, donc appartient à $ C$. Il en résulte que $ \hat A$ est inclus dans $ C$ pour tout $ C\in\mathcal C_A$, et est donc inclus dans $ \Conv (A)$, d'où $ \hat A=\Conv (A)$.$ \square$

Exemples : l'enveloppe convexe de deux points $ A$ et $ B$ est le segment $ [AB]$ ; l'enveloppe convexe de 3 points $ A$, $ B$, $ C$ du plan est le triangle plein $ ABC$.

Demi-espaces, régionnement

L'exemple des demi-droites n'est qu'un cas particulier d'un exemple fondamental de convexes : les demi-espaces. Si $ E$ est un espace affine de dimension $ n$ et $ H$ un hyperplan affine, $ H$ sépare l'espace en deux, comme le montre la proposition suivante :

Proposition 17   Soit $ E$ un espace affine et $ H$ un hyperplan affine de $ E$. La relation $ \mathcal R$ définie par « $ A\mathcal R B$ si et seulement si $ [AB]\cap H=\emptyset$» est une relation d'équivalence sur le complémentaire $ E\setminus H$ de $ H$ dans $ E$ qui partage $ E\setminus H$ en exactement deux classes.

Ces classes sont appelés demi-espaces ouverts délimités par $ H$. Les demi-espaces fermés sont obtenus en prenant leurs réunions avec $ H$. Si deux points $ A$ et $ B$ sont en relation par $ \mathcal R$, on dit que $ A$ et $ B$ sont du même côté de $ H$.

Démonstration : Soit $ (O,\vec e_1,\dots ,\vec e_n)$ un repère cartésien de $ E$ dont l'origine $ O$ appartient à $ H$ et les vecteurs $ \vec e_1,\dots,\vec e_{n-1}$ appartiennent à l'hyperplan vectoriel $ \overrightarrow{H}$. L'hyperplan $ H$ admet $ x_n=0$ comme équation cartésienne dans ce repère. Soient $ A$ et $ B$ deux points de $ E$ n'appartenant pas à $ H$, de coordonnées respectives $ (a_1,\dots,a_n)$ et $ (b_1,\dots,b_n)$ dans ce repère. On a donc $ a_n b_n \not =0$. Tout point $ M$ du segment $ [AB]$ s'écrit $ \alpha A+(1-\alpha)B$ pour un $ \alpha\in[0,1]$. Ce point appartient à $ H$ si et seulement si $ \alpha a_n+(1-\alpha) b_n=0$, soit encore $ \alpha (b_n-a_n)=b_n$. Cette équation en $ \alpha$ admet une solution dans $ [0,1]$ si et seulement si $ a_n$ et $ b_n$ sont de signes opposés. Le segment $ [AB]$ rencontre donc $ H$ si et seulement si $ a_nb_n<0$. Autrement dit, $ A\mathcal R B$ si et seulement si $ a_n$ et $ b_n$ sont de même signe. Il en résulte immédiatement que la relation $ \mathcal R$ est une relation d'équivalence sur $ E\setminus H$ et que les deux classes d'équivalence pour $ \mathcal R$ sont $ \{M\in E \mid x_n>0\}$ et $ \{M\in E \mid x_n<0\}$.$ \square$

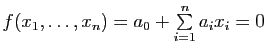Si $ f(x_1,\dots,x_n)=a_0+\sum\limits_{i=1}^n a_ix_i=0$ est une équation cartésienne de $ H$, ces demi-espaces sont définis par les inéquations $ f(x_1,\dots,x_n)>0$ et $ f(x_1,\dots,x_n)<0$.

Polyèdres convexes

Définition 16   On appelle polyèdre convexe toute partie bornée non vide d'un espace affine qui peut s'écrire comme intersection d'un nombre fini de demi-espaces fermés.

Dans le plan, on retrouve la notion usuelle de polygone convexe plein. Dans l'espace de dimension 3, un polyèdre est un solide convexe d'intérieur non vide (s'il n'est pas contenu dans un plan). On remarque que cette définition exclut le cas des dièdres ou des trièdres, qui sont intersection de deux ou trois demi-espaces fermés mais ne sont pas bornés.

On aurait pu donner une autre définition d'un polyèdre convexe, comme le montre la proposition suivante, que nous ne démontrerons pas :

Proposition 18   Une partie d'un espace affine $ E$ est un polyèdre convexe si et seulement si elle est l'enveloppe convexe d'un nombre fini de points de $ E$.

Il résulte immédiatement de la définition que toute intersection d'un polyèdre convexe et d'un sous-espace affine est vide ou est un polyèdre convexe (un sous-espace affine peut s'écrire comme intersection d'un nombre fini d'hyperplans affines et un hyperplan affine est l'intersection des deux demi-espaces fermés qu'il limite). De même toute intersection d'un nombre fini de polyèdres convexes est vide ou est un polyèdre convexe.

Un exemple de polyèdre convexe en dimension quelconque est le $ n$-simplexe

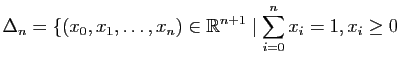$\displaystyle \Delta_n=\{(x_0,x_1,\dots,x_n)\in \mathbb{R}^{n+1} \mid \sum_{i=0}^{n} x_i=1, x_i \geq 0$    pour tout $\displaystyle i=0,\dots, n\} \; .$

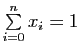($ \Delta_n$ est une partie de $ \mathbb{R}^{n+1}$, mais il est inclus dans l'hyperplan d'équation $ \sum\limits_{i=0}^{n} x_i=1$, si bien que sa dimension intrinsèque est $ n$.)

Polyèdres dans l'espace de dimension 3

Théorème 1   Théorème de structure des polyèdres convexes

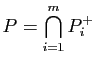Pour tout polyèdre convexe d'intérieur non vide $ P$ de l'espace de dimension 3, il existe une écriture minimale (au sens du nombre de termes) $ \displaystyle P=\bigcap_{i=1}^m P_i^+$ de $ P$ comme intersection de demi-espaces fermés. Cette écriture est unique à l'ordre près. L'intersection de $ P$ avec chacun des plans $ P_i$ est un polygone convexe plein d'intérieur non vide dans $ P_i$. Ces polygones sont appelés faces du polyèdre. Les côtés de ces polygones sont appelés arêtes du polyèdre et leurs sommets sommets du polyèdre.

Théorème 2   Formule d'Euler

Pour tout polyèdre convexe $ P$ de l'espace de dimension 3, on a :

$\displaystyle s-a+f=2$

où $ s$ est le nombre de sommets, $ a$ le nombre d'arêtes et $ f$ le nombre de faces de $ P$.

Nous ne démontrerons pas ces deux théorèmes (voir néanmoins la section 3.6 dans la partie Compléments), pas plus que la proposition suivante.

Proposition 19   Tout polyèdre convexe est l'enveloppe convexe de ses sommets.

Définition 17   On appelle tétraèdre (plein) l'enveloppe convexe de quatre points non coplanaires.

Un tétraèdre possède 4 sommets, 4 faces et 6 arêtes. Ses faces sont des triangles. Si ces triangles sont tous équilatéraux, le tétraèdre est dit régulier. Un tétraèdre est donc régulier si et seulement si toutes ses arêtes ont même longueur (cette définition, comme d'autres qui suivront, suppose l'espace affine muni d'une structure euclidienne).

Définition 18   Soit $ (A,\vec{i},\vec{j},\vec{k})$ un repère cartésien (non nécessairement orthonormé) de l'espace. On appelle parallélépipède (plein) construit sur ce repère l'ensemble des points de l'espace dont les trois coordonnées dans ce repère appartiennent toutes à l'intervalle $ [0,1]$.

Figure 2: Parallélépipède
\includegraphics[width=8cm]{figures/parallelepipede}

Un parallélépipède a 8 sommets, 6 faces et 12 arêtes. Ses faces sont des parallélogrammes. Les sommets du parallélépipède construit sur un repère cartésien sont les points de coordonnées toutes égales à 0 ou 1 dans ce repère, ses faces sont portées par les plans d'équations $ x=0$, $ x=1$, $ y=0$, $ y=1$, $ z=0$, $ z=1$.

Un parallélépipède dont les faces sont des rectangles est appelé parallélépipède rectangle.

Un cube est un parallélépipède dont les faces sont des carrés.

Figure 3: Pyramide et prisme
\includegraphics[width=0.45\textwidth]{figures/pyramide} \includegraphics[width=0.45\textwidth]{figures/prisme}

Une pyramide est l'enveloppe convexe d'un polygone plan convexe non aplati, appelé base de la pyramide, et d'un point $ S$ (le sommet de la pyramide) n'appartenant pas au plan de ce polygone.

Une pyramide dont la base a $ n$ sommets a $ n+1$ faces, $ 2n$ arêtes et $ n+1$ sommets. Un tétraèdre est une pyramide ayant pour base un triangle.

Une pyramide régulière est une pyramide dont la base est un polygone régulier convexe et dont le sommet appartient à la droite perpendiculaire à la base menée par le centre de ce polygone.

Un prisme est l'enveloppe convexe de deux polygones plans convexes, appelés bases du prisme, déduits l'un de l'autre par une translation de vecteur n'appartenant pas à la direction commune de leurs plans. Le prisme est dit droit si le vecteur de la translation est orthogonal aux plans des bases.

Un prisme dont les bases ont chacune $ n$ sommets a $ n+2$ faces, $ 3n$ arêtes et $ 2n$ sommets. Toutes les faces d'un prisme autres que les bases sont des parallélogrammes. Si le prisme est droit, ces faces sont des rectangles. Un parallélépipède est un prisme ayant pour base un parallélogramme.


Section : Cours
Avant : Repérage
Après : Applications affines


         © UJF Grenoble, 2011                              Mentions légales