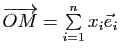 . Ces nombres sont appelés coordonnées cartésiennes de
. Ces nombres sont appelés coordonnées cartésiennes de 1) Coordonnées cartésiennes
Repères cartésiens
On a déjà remarqué que le choix d'une origine ![]() permet d'identifier un espace affine
permet d'identifier un espace affine ![]() de dimension
de dimension ![]() à sa direction
à sa direction
![]() , c'est-à-dire à un espace vectoriel. Le choix d'une base
, c'est-à-dire à un espace vectoriel. Le choix d'une base
![]() de
de
![]() permet d'identifier cet espace vectoriel à
permet d'identifier cet espace vectoriel à
![]() . Le couple
. Le couple
![]() est appelé repère cartésien de
est appelé repère cartésien de ![]() . Pour tout point
. Pour tout point ![]() de
de ![]() , il existe alors un unique
, il existe alors un unique ![]() -uplet
-uplet
![]() de réels vérifiant
de réels vérifiant
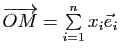 . Ces nombres sont appelés coordonnées cartésiennes de
. Ces nombres sont appelés coordonnées cartésiennes de ![]() dans le repère
dans le repère
![]() . Si
. Si ![]() , on notera souvent ces coordonnées
, on notera souvent ces coordonnées ![]() et, si
et, si ![]() ,
, ![]() .
.
Mesure algébrique
Un repère cartésien d'une droite affine ![]() est un couple
est un couple ![]() , où
, où ![]() est un point de
est un point de ![]() et
et ![]() un vecteur non nul de
un vecteur non nul de
![]() (on dit que
(on dit que ![]() est un vecteur directeur de
est un vecteur directeur de ![]() ). Si
). Si ![]() et
et ![]() sont deux points de
sont deux points de ![]() , le vecteur
, le vecteur
![]() s'écrit de manière unique
s'écrit de manière unique
![]() pour un réel
pour un réel ![]() . Ce réel
. Ce réel ![]() est appelé mesure algébrique de
est appelé mesure algébrique de ![]() et noté
et noté
![]() . La mesure algébrique
. La mesure algébrique
![]() dépend donc du choix d'un vecteur directeur de
dépend donc du choix d'un vecteur directeur de ![]() : si on remplace
: si on remplace ![]() par
par
![]() , où
, où ![]() est un réel non nul, toutes les mesures algébriques sur
est un réel non nul, toutes les mesures algébriques sur ![]() sont divisées par
sont divisées par ![]() . Mais le rapport
. Mais le rapport
![]() de mesures algébriques de couples de points de
de mesures algébriques de couples de points de ![]() ne dépend pas du choix du vecteur directeur : il est donc défini de manière intrinsèque.
ne dépend pas du choix du vecteur directeur : il est donc défini de manière intrinsèque.
Equation d'un hyperplan
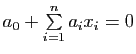 , où les
, où les 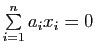 dans la base
dans la base
Il en résulte que deux hyperplans ![]() et
et ![]() , d'équations respectives
, d'équations respectives
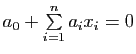 et
et
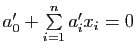 , sont parallèles si et seulement si les
, sont parallèles si et seulement si les ![]() -uplets
-uplets
![]() et
et
![]() de réels sont proportionnels.
de réels sont proportionnels.
Démonstration : Soit ![]() un hyperplan de
un hyperplan de ![]() ,
, ![]() un point de
un point de ![]() de coordonnées
de coordonnées
![]() dans le repère
dans le repère
![]() , et
, et
![]() , où les
, où les ![]() sont des réels non tous nuls, une équation de l'hyperplan vectoriel
sont des réels non tous nuls, une équation de l'hyperplan vectoriel
![]() dans la base
dans la base
![]() de
de
![]() . Un point
. Un point ![]() de
de ![]() de coordonnées
de coordonnées
![]() appartient à
appartient à ![]() si et seulement si le vecteur
si et seulement si le vecteur
![]() appartient à
appartient à
![]() , i.e. si et seulement si
, i.e. si et seulement si
![]() . Il en résulte que
. Il en résulte que
![]() , où
, où
![]() , est une équation de
, est une équation de ![]() dans le repère
dans le repère
![]() .
.
Réciproquement, soient
![]() des réels vérifiant
des réels vérifiant
![]() et
et ![]() un point de coordonnées
un point de coordonnées
![]() vérifiant
vérifiant
![]() (un tel point existe puisque
(un tel point existe puisque
![]() ne sont pas tous nuls). L'équation
ne sont pas tous nuls). L'équation
![]() s'écrit encore
s'écrit encore
![]() et signifie que le vecteur
et signifie que le vecteur
![]() appartient à l'hyperplan vectoriel
appartient à l'hyperplan vectoriel
![]() d'équation
d'équation
![]() . Cette équation est donc celle de l'hyperplan affine passant par
. Cette équation est donc celle de l'hyperplan affine passant par ![]() et de direction
et de direction
![]() .
.
Deux hyperplans affines d'équations
![]() et
et
![]() sont parallèles s'ils ont même direction, i.e. si les hyperplans vectoriels d'équations
sont parallèles s'ils ont même direction, i.e. si les hyperplans vectoriels d'équations
![]() et
et
![]() sont confondus, ou encore si et seulement si les
sont confondus, ou encore si et seulement si les ![]() -uplets
-uplets
![]() et
et
![]() de réels sont proportionnels. Ils sont confondus si
de réels sont proportionnels. Ils sont confondus si
![]() et
et
![]() sont proportionnels, sinon ils sont strictement parallèles.
sont proportionnels, sinon ils sont strictement parallèles.![]()
Equations de droites et de plans en dimensions 2 et 3
Une droite a donc, dans un repère cartésien du plan, une équation de la forme ![]() , avec
, avec
![]() , et un plan, dans un repère cartésien de l'espace, une équation de la forme
, et un plan, dans un repère cartésien de l'espace, une équation de la forme
![]() , avec
, avec
![]() .
.
Attention : une droite de l'espace est représentée par un système de deux équations (celles de deux plans distincts la contenant).
2) Coordonnées barycentriques
Une autre façon de repérer les points dans un espace affine consiste à les écrire comme barycentres de points d'un repère : par exemple, si ![]() et
et ![]() sont deux points distincts d'une droite
sont deux points distincts d'une droite ![]() , tout point de
, tout point de ![]() s'écrit comme barycentre de
s'écrit comme barycentre de ![]() et
et ![]() , et cette écriture est unique à condition de normaliser les coefficients en imposant à leur somme de valoir 1.
, et cette écriture est unique à condition de normaliser les coefficients en imposant à leur somme de valoir 1.
Démonstration : Si (i) est vérifiée, et si ![]() appartenait au sous-espace affine engendré par
appartenait au sous-espace affine engendré par
![]() ,
, ![]() serait barycentre des points
serait barycentre des points
![]() affectés de coefficients
affectés de coefficients
![]() de somme non nulle (proposition 8), d'où
de somme non nulle (proposition 8), d'où
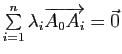 ; la famille
; la famille
![]() ne serait donc pas libre, ce qui contredirait (i).
ne serait donc pas libre, ce qui contredirait (i).
De même, si (i) était vérifiée, et si ![]() appartenait au sous-espace affine engendré par
appartenait au sous-espace affine engendré par
![]() ,
, ![]() serait barycentre de ces points affectés de coefficients
serait barycentre de ces points affectés de coefficients
![]() de somme non nulle ; le vecteur
de somme non nulle ; le vecteur
![]() serait donc combinaison linéaire des vecteurs
serait donc combinaison linéaire des vecteurs
![]() et on conclut comme précédemment.
et on conclut comme précédemment.
On a donc montré que (i) impliquait (ii).
Si (i) n'est pas vérifiée, la famille de ![]() vecteurs
vecteurs
![]() n'étant pas une base de
n'étant pas une base de ![]() n'est pas libre, puisque
n'est pas libre, puisque ![]() est la dimension de
est la dimension de ![]() . Il existe donc des réels
. Il existe donc des réels
![]() non tous nuls tels que
non tous nuls tels que
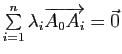 .
Si
.
Si
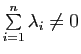 , cette relation montre que
, cette relation montre que ![]() est barycentre des points
est barycentre des points
![]() et appartient donc au sous-espace affine engendré par ces points. Si
et appartient donc au sous-espace affine engendré par ces points. Si
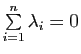 , en supposant
, en supposant
![]() pour fixer les idées, on aurait
pour fixer les idées, on aurait
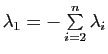 , d'où
, d'où
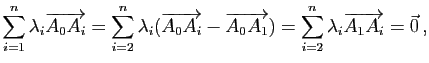
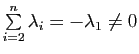 ) et appartient donc au sous-espace affine de
) et appartient donc au sous-espace affine de
Remarque : La condition (i) fait jouer un rôle particulier au point ![]() ; l'équivalence avec la seconde condition montre qu'en fait tous les points
; l'équivalence avec la seconde condition montre qu'en fait tous les points ![]() jouent le même rôle : on aurait donc pu rajouter dans l'énoncé
jouent le même rôle : on aurait donc pu rajouter dans l'énoncé ![]() conditions équivalentes à la première en permutant
conditions équivalentes à la première en permutant ![]() avec l'un des points
avec l'un des points
![]() .
.
Attention : un repère affine d'un espace affine ![]() de dimension
de dimension ![]() est donc une famille de
est donc une famille de ![]() points de
points de ![]() (2 points distincts pour une droite, les sommets d'un triangle non aplati pour un plan, les sommets d'un tétraèdre non aplati pour l'espace de dimension 3).
(2 points distincts pour une droite, les sommets d'un triangle non aplati pour un plan, les sommets d'un tétraèdre non aplati pour l'espace de dimension 3).
Démonstration : Soit
![]() une famille de réels de somme 1. Le point
une famille de réels de somme 1. Le point ![]() est barycentre du système pondéré
est barycentre du système pondéré
![]() si et seulement si
si et seulement si
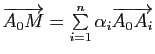 .
Or la famille
.
Or la famille
![]() étant une base de
étant une base de
![]() , il existe un
, il existe un ![]() -uplet
-uplet
![]() de réels et un seul tel que
de réels et un seul tel que
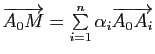 . Le point
. Le point ![]() est donc barycentre du système pondéré
est donc barycentre du système pondéré
![]() où
où
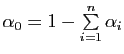 . Si
. Si ![]() est barycentre du système pondéré
est barycentre du système pondéré
![]() avec
avec
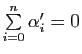 , alors
, alors
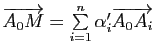 , d'où
, d'où
![]() pour
pour
![]() et
et
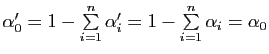 .
.![]()
Le point ![]() s'écrit donc
s'écrit donc
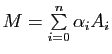 , avec
, avec
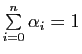 . Par homogénéité du barycentre,
. Par homogénéité du barycentre, ![]() est aussi barycentre du système
est aussi barycentre du système
![]() pour tout réel non nul
pour tout réel non nul ![]() . On dit parfois que les
. On dit parfois que les
![]() constituent un système de coordonnées barycentriques homogènes de
constituent un système de coordonnées barycentriques homogènes de ![]() dans le repère affine
dans le repère affine
![]() ; les
; les ![]() sont alors appelés coordonnées barycentriques réduites ou normalisées de
sont alors appelés coordonnées barycentriques réduites ou normalisées de ![]() dans ce repère.
dans ce repère.
La figure GeoGebra donne les coordonnées barycentriques normalisées du point ![]() dans le repère affine
dans le repère affine ![]() . Vous pouvez déplacer le point
. Vous pouvez déplacer le point ![]() et déformer le triangle
et déformer le triangle ![]() .
.
La démonstration de la proposition 12 montre que l'on passe très facilement des coordonnées cartésiennes dans un repère
![]() aux coordonnées barycentriques dans le repère affine
aux coordonnées barycentriques dans le repère affine
![]() : si
: si
![]() sont les coordonnées cartésiennes de
sont les coordonnées cartésiennes de ![]() dans le repère
dans le repère
![]() , alors
, alors
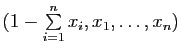 sont les coordonnées barycentriques de
sont les coordonnées barycentriques de ![]() dans le repère affine
dans le repère affine
![]() .
.
Réciproquement, si
![]() sont les coordonnées barycentriques de
sont les coordonnées barycentriques de ![]() dans le repère affine
dans le repère affine
![]() , les coordonnées cartésiennes de
, les coordonnées cartésiennes de ![]() dans le repère cartésien
dans le repère cartésien
![]() sont
sont
![]() .
.
On en déduit immédiatement l'équation barycentrique d'un hyperplan affine.
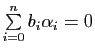 , où
, où
Démonstration : On a vu à la proposition 10 que tout hyperplan affine admettait dans le repère cartésien
![]() une équation de la forme
une équation de la forme
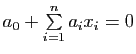 , où
, où
![]() sont des réels non tous nuls et
sont des réels non tous nuls et
![]() les coordonnées cartésiennes d'un point générique
les coordonnées cartésiennes d'un point générique ![]() . En remarquant que
. En remarquant que
![]() pour
pour
![]() et
et
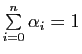 , cette équation s'écrit
, cette équation s'écrit
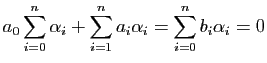
On remarque que cette équation est valable tant pour des coordonnées barycentriques normalisées (
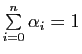 ) que pour des coordonnées barycentriques quelconques (
) que pour des coordonnées barycentriques quelconques (
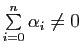 ).
).
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales