Sous-espaces affines

Définition 7 Une partie d'un espace affine est un sous-espace affine de s'il existe un point de tel que $\overrightarrow{F}=\{ \overrightarrow{AM} \mid M\in F\}$ soit un sous-espace vectoriel de $\overrightarrow{E}$ .

Notation 2 Pour tout point de et tout sous-espace vectoriel $\overrightarrow{F}$ de $\overrightarrow{E}$ , l'ensemble

$\displaystyle \Aff (A,\overrightarrow{F})=\{ A+\u\mid \u\in\overrightarrow{F}\}$

est un sous-espace affine de . On l'appellera sous-espace affine de passant par de direction $\overrightarrow{F}$ . Si $\u$ est un vecteur non nul de $\overrightarrow{E}$ , on notera $D(A,\u)$ la droite affine passant par et de direction la droite vectorielle $\mathbb{R}\u$ . De même, si $\u$ et $\v$ sont deux vecteurs linéairement indépendants, on notera $P(A,\u,\v)$ le plan affine passant par et de direction le plan vectoriel $\mathbb{R}\u\oplus\mathbb{R}\v$ engendré par les deux vecteurs $\u$ et $\v$ .

Proposition 5 Soit $F=\Aff (A,\overrightarrow{F})$ un sous-espace affine de . On a alors, pour tout point de , $\{ \overrightarrow{BM} \mid M\in F\}=\overrightarrow{F}$ .

Démonstration : Puisque

appartient à

, le vecteur $\overrightarrow{AB}$ appartient à $\overrightarrow{F}$ . Or $\overrightarrow{BM}=\overrightarrow{AM}-\overrightarrow{AB}$ et l'application $\u\mapsto \u-\overrightarrow{AB}$ est une bijection de $\overrightarrow{F}$ sur $\overrightarrow{F}$ , puisque $\overrightarrow{F}$ est un sous-espace vectoriel de $\overrightarrow{E}$ . Il en résulte que

$\displaystyle \{ \overrightarrow{BM} \mid M\in F\}=\{ \overrightarrow{AM}-\over... ...{ \u-\overrightarrow{AB} \mid \u\in \overrightarrow{F}\}=\overrightarrow{F}\; .$

Le sous-espace vectoriel $\overrightarrow{F}$ de $\overrightarrow{E}$ ne dépend donc pas du choix de

dans

. On l'appelle direction du sous-espace affine

. La restriction de l'application $(M,N) \longmapsto \overrightarrow{MN}$ à $F\times F$ munit

d'une structure naturelle d'espace affine de direction $\overrightarrow{F}$ . Sa dimension $\dim(F)$ est celle de $\overrightarrow{F}$ .

Un sous-espace affine de dimension 0 est constitué d'un point, un sous-espace affine de dimension 1 est une droite, un sous-espace affine de dimension 2 un plan.

Démonstration : Si

est un sous-espace affine de

un point de

et $(A_i,\lambda_i)_{i=1,\dots,n}$ un système de points pondérés de

de poids total non nul, le barycentre

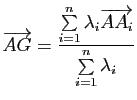de ce système vérifie $\overrightarrow{AG}=\dfrac{\sum\limits_{i=1}^n \lambda_i\overrightarrow{AA_i}}{\sum\limits_{i=1}^n \lambda_i}$ . Il en résulte que $\overrightarrow{AG}$ appartient à $\overrightarrow{F}$ , puisque $\overrightarrow{F}$ est un sous-espace vectoriel de $\overrightarrow{E}$ , et donc que

appartient à

Réciproquement, soit

une partie non vide de

telle que tout barycentre de points de

affectés de coefficients quelconques (de somme non nulle) appartient à

, et

un point de

. Pour tout couple

de points de

et tout couple $(\lambda,\mu)$ de réels, le point

défini par $\overrightarrow{AP}=\lambda \overrightarrow{AM}+\mu \overrightarrow{AN}$ est le barycentre du système de points pondérés $[(A, 1-\lambda-\mu), (M,\lambda), (N,\mu)]$ et appartient donc à

. Il en résulte que $\overrightarrow{F}=\{ \overrightarrow{AM} \mid M\in F\}$ est un sous-espace vectoriel de $\overrightarrow{E}$ ( $\vec{0}=\overrightarrow{AA}$ appartient à $\overrightarrow{F}$ , qui n'est donc pas vide), et donc que

est un sous-espace affine de

. $\square$

Définition 9 Deux sous-espaces affines et d'un même espace affine sont dits parallèles s'ils ont même direction : $\overrightarrow{F}=\overrightarrow{G}$ .

Le parallélisme est une relation d'équivalence sur l'ensemble des sous-espaces affines de

. Deux sous-espaces affines parallèles, au sens de cette définition, ont même dimension.

Si deux sous-espaces affines

d'un même espace affine

vérifient $\overrightarrow{F}\subset \overrightarrow{G}$ , on dit que

est parallèle à

(ou parfois faiblement parallèle à

); cette relation n'est naturellement pas symétrique.

Proposition 7 L'intersection de toute famille (finie ou infinie) de sous-espaces affines d'un même espace affine est soit vide, soit un sous-espace affine de direction l'intersection des directions de ces sous-espaces affines.

Démonstration : Soit $(F_i)_{i\in I}$ une famille de sous-espaces affines de

. Si l'intersection $\bigcap\limits_{i\in I} F_i$ de cette famille est vide, il n'y a rien à démontrer. Sinon, soit

un point de cette intersection. Pour tout $i\in I$ , un point

appartient à

si et seulement si le vecteur $\overrightarrow{AM}$ appartient à la direction $\overrightarrow{F}_i$ de

, puisque

appartient à

. Il en résulte que

appartient à $\bigcap\limits_{i\in I} F_i$ si et seulement si $\overrightarrow{AM}$ appartient au sous-espace vectoriel $\bigcap\limits_{i\in I} \overrightarrow{F}_i$ de $\overrightarrow{E}$ , ce qui montre que $\bigcap\limits_{i\in I} F_i$ est un sous-espace affine de

de direction $\bigcap\limits_{i\in I} \overrightarrow{F}_i$ . $\square$

Définition 10 Soit une partie non vide d'un espace affine . On appelle sous-espace affine engendré par l'intersection de tous les sous-espaces affines de contenant .

Proposition 8 Le sous-espace affine engendré par une partie non vide d'un espace affine est le plus petit (au sens de l'inclusion) sous-espace affine de contenant . C'est aussi l'ensemble de tous les barycentres de tous les systèmes de points pondérés de affectés de coefficients quelconques (de somme non nulle).

Démonstration : Soit

une partie non vide de

le sous-espace affine de

engendré par

est non vide, car il contient

, et c'est un sous-espace affine, comme intersection de sous-espaces affines . Par définition, il est inclus dans tout sous-espace affine de

contenant

, c'est donc bien le plus petit sous-espace affine de

contenant

Soit

l'ensemble de tous les barycentres de tous les systèmes de points pondérés de

affectés de coefficients quelconques (de somme non nulle).

n'est pas vide, car il contient

(considérer un système réduit à un point), et tout barycentre d'un système de points pondérés de

appartient encore à

par associativité du barycentre. Il résulte de la proposition 6 que

est un sous-espace affine de

. Comme il contient

, il contient

. Mais

est un sous-espace affine de

et tout point de

appartient à

. Il en résulte que tout barycentre de points de

appartient à

, donc que

est inclus dans

. On a donc

. $\square$

Proposition 9 Soient et deux sous-espaces affines d'un espace affine , un point de et un point de . L'intersection $F \cap G$ est non vide si et seulement si le vecteur $\overrightarrow{AB}$ appartient à la somme $\overrightarrow{F}+ \overrightarrow{G}$ des directions de ces deux sous-espaces. En particulier, si $\overrightarrow{F}$ et $\overrightarrow{G}$ sont deux sous-espaces vectoriels supplémentaires de $\overrightarrow{E}$ , l'intersection $F \cap G$ consiste en un point.

Démonstration : Si l'intersection $F \cap G$ n'est pas vide, soit

un point de cette intersection. Le vecteur $\overrightarrow{AI}$ appartient à $\overrightarrow{F}$ et le vecteur $\overrightarrow{IB}$ à $\overrightarrow{G}$ . Il en résulte que le vecteur $\overrightarrow{AB}=\overrightarrow{AI}+\overrightarrow{IB}$ appartient à $\overrightarrow{F}+ \overrightarrow{G}$ .

Réciproquement, si $\overrightarrow{AB}$ appartient à $\overrightarrow{F}+ \overrightarrow{G}$ , il existe un vecteur $\u$ de $\overrightarrow{F}$ et un vecteur $\v$ de $\overrightarrow{G}$ tels que $\overrightarrow{AB}=\u+\v$ . Soit

le point de

défini par $\overrightarrow{AI}=\u$ . Le point

appartient à

puisque $\overrightarrow{AI}$ appartient à $\overrightarrow{F}$ . L'égalité

Dans le cas où $\overrightarrow{F}$ et $\overrightarrow{G}$ sont des sous-espaces vectoriels supplémentaires de $\overrightarrow{E}$ , tout vecteur de $\overrightarrow{E}$ , en particulier le vecteur $\overrightarrow{AB}$ , appartient à $\overrightarrow{E}=\overrightarrow{F}+ \overrightarrow{G}$ . L'intersection $F \cap G$ n'est donc pas vide, et sa direction est $\overrightarrow{F}\cap \overrightarrow{G}= \{\vec{0}\}$ (proposition 7). Cette intersection est donc réduite à un point. $\square$