La notion de barycentre est essentielle en géométrie affine. Elle joue un rôle identique à celui que tient la notion de combinaison linéaire en algèbre linéaire.
À tout système de points pondérés de ![]() , on associe une fonction
, on associe une fonction ![]() de
de ![]() dans
dans
![]() , appelée fonction vectorielle de Leibniz du système, par :
, appelée fonction vectorielle de Leibniz du système, par :
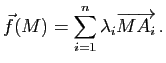
Démonstration : Soit ![]() un point fixé de
un point fixé de ![]() . On a pour tout point
. On a pour tout point ![]() de
de ![]() :
:
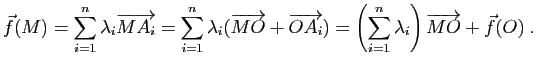
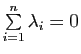 , alors
, alors
![$ \overrightarrow{OM}=\dfrac{1}{\sum\limits_{i=1}^n \lambda_i} \left[ \vec{f}(O)-\u\right]$](img87.gif) .
.
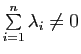 . On appelle barycentre de ce système l'unique point
. On appelle barycentre de ce système l'unique point 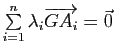 .
.
Le barycentre d'un système de points pondérés n'est donc défini que si le poids total du système n'est pas nul.
Propriétés du barycentre
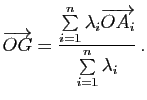
Démonstration : Les deux premières propriétés sont évidentes. Pour démontrer la troisième, soit ![]() le barycentre du système pondéré
le barycentre du système pondéré
![]() . Il suffit de considérer (en réordonnant éventuellement les points) le cas où les points que l'on regroupe sont
. Il suffit de considérer (en réordonnant éventuellement les points) le cas où les points que l'on regroupe sont
![]() avec
avec
![]() . En notant
. En notant ![]() le barycentre du système pondéré
le barycentre du système pondéré
![]() , on a alors
, on a alors
![]() et
et
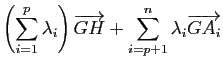 |
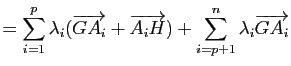 |
|
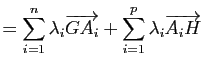 |
||
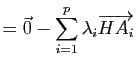 |
||
La dernière propriété provient de la relation
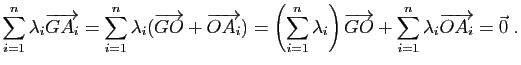
La notion de milieu est donc purement affine et ne fait pas appel à la notion de distance, ce qui n'empêche naturellement pas le milieu ![]() d'un couple
d'un couple ![]() de points d'être caractérisé, en géométrie euclidienne, par la double égalité
de points d'être caractérisé, en géométrie euclidienne, par la double égalité
![]() .
.
Notations de Grassmann
Si
![]() est un système de points pondérés d'un espace affine
est un système de points pondérés d'un espace affine ![]() de poids total
de poids total
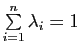 , le barycentre
, le barycentre ![]() de ce système vérifie
de ce système vérifie
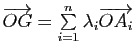 pour tout point
pour tout point ![]() de
de ![]() . On le notera
. On le notera
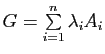 .
.
On définit ainsi sans se référer à une origine un calcul sur les points qui satisfait aux règles habituelles du calcul vectoriel. Par exemple, si ![]() est l'isobarycentre des sommets d'un triangle
est l'isobarycentre des sommets d'un triangle ![]() , on peut écrire
, on peut écrire
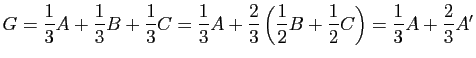
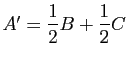 est le milieu de
est le milieu de
Mais attention : cette notation (parfois appelée notation de Grassmann) n'a de sens que pour un système de points pondérés de poids total 1. L'écriture ![]() ou
ou ![]() (où
(où ![]() est un point) n'a pas de sens.
est un point) n'a pas de sens.
On a par ailleurs vu, en étudiant la fonction vectorielle de Leibniz, que si
![]() est un système de points pondérés de poids total nul :
est un système de points pondérés de poids total nul :
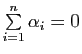 , le vecteur
, le vecteur ![]() défini par
défini par
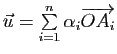 ne dépend pas du choix de
ne dépend pas du choix de ![]() . On peut donc noter également
. On peut donc noter également
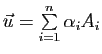 . Par exemple, si
. Par exemple, si ![]() ,
,
![]() et
et
![]() ,
, ![]() est le vecteur
est le vecteur
![]() .
Mais une expression telle que
.
Mais une expression telle que ![]() , ou
, ou ![]() , ou
, ou
![]() , ne représente ni un point ni un vecteur.
, ne représente ni un point ni un vecteur.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales