Section : Compléments
Avant : Desargues dans le plan et
Après : La formule d'Euler pour les

Birapport

On a vu à l'exercice 32 qu'étant donné deux triplets $ (D_1,D_2,D_3)$ et $ (D'_1,D'_2,D'_3)$ de droites distinctes et concourantes d'un même plan affine, il existait toujours une transformation affine de ce plan transformant $ D_1$ en $ D'_1$, $ D_2$ en $ D'_2$ et $ D_3$ en $ D'_3$. Du point de vue de la géométrie affine, tous les triplets de droites distinctes et concourantes sont donc équivalents (de même que tous les triangles non aplatis le sont, puisque, étant donné deux triangles non aplatis $ ABC$ et $ A'B'C'$, il existe toujours une transformation affine du plan et une seule transformant $ A$ en $ A'$, $ B$ en $ B'$ et $ C$ en $ C'$).

Il n'en va plus de même si on considère des quadruplets de droites concourantes. On peut en effet associer à tout tel quadruplet un nombre, appelé birapport ou rapport anharmonique des quatre droites, qui est invariant par toute transformation affine.

On commence par définir le birapport $ [A,B,C,D]$ de quatre points distincts alignés $ A$, $ B$, $ C$, $ D$ comme le réel

$\displaystyle [A,B,C,D]=\dfrac{\overline {AC} \; \overline {BD}}{\overline {AD} \; \overline {BC}}\; .$

Ce réel ne dépend pas du choix du vecteur directeur de la droite portant ces points, mais il dépend de l'ordre des points.

Soit maintenant, dans un plan affine $ E$, quatre droites distinctes concourantes en un même point $ O$ et coupant deux droites $ \Delta$ et $ \Delta'$ en des points $ A$, $ B$, $ C$, $ D$ et $ A'$, $ B'$, $ C'$, $ D'$. Orientons $ E$ et munissons-le d'un produit scalaire. Soit alors $ H$ le projeté orthogonal de $ O$ sur $ \Delta$ et $ \v$ un vecteur directeur unitaire de $ \Delta$ tel que le système $ (\overrightarrow{OH},\v)$ soit direct. On a alors, en prenant les déterminants dans une base orthonormée directe :

$\displaystyle \mathrm{det}(\overrightarrow{OA},\overrightarrow{OC})$ $\displaystyle =OA \times OC \times \sin(\overrightarrow{OA},\overrightarrow{OC})$    
  $\displaystyle =\mathrm{det}(\overrightarrow{OH}+\overrightarrow{HA},\overrightarrow{OH}+\overrightarrow{HC})$    
  $\displaystyle =\mathrm{det}(\overrightarrow{OH},\overrightarrow{HC})+\mathrm{det}(\overrightarrow{HA},\overrightarrow{OH})$    
  $\displaystyle =\mathrm{det}(\overrightarrow{OH},\overrightarrow{AH}+\overrightarrow{HC})$    
  $\displaystyle =\mathrm{det}(\overrightarrow{OH},\overrightarrow{AC})$    
  $\displaystyle =OH\times \overline {AC} ,$    

ce nombre étant le double de l'aire algébrique du triangle $ OAC$.

\includegraphics[width=0.6\textwidth]{figures/birapport}

Il en résulte que

$\displaystyle [A,B,C,D]=\dfrac{\sin(\overrightarrow{OA},\overrightarrow{OC}) \;... ...{OA},\overrightarrow{OD}) \; \sin(\overrightarrow{OB},\overrightarrow{OC})}\; .$

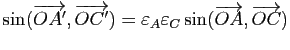Mais $ \sin(\overrightarrow{OA'},\overrightarrow{OC'})=\varepsilon_A \varepsilon_C \sin(\overrightarrow{OA},\overrightarrow{OC})$, où $ \varepsilon_A$ (resp. $ \varepsilon_C$) vaut $ 1$ si les points $ A$ et $ A'$ (resp. $ C$ et $ C'$) sont du même côté de $ O$, $ -1$ sinon. En écrivant des formules analogues pour les autres termes, on en déduit que $ [A,B,C,D]=[A',B',C',D']$. Ce nombre ne dépend donc pas de la sécante $ \Delta$. On l'appelle birapport des quatre droites $ (OA)$, $ (OB)$, $ (OC)$, $ (OD)$. Comme toute transformation affine conserve les rapports de mesures algébriques pour des points alignés, elle conserve a fortiori le birapport.


Section : Compléments
Avant : Desargues dans le plan et
Après : La formule d'Euler pour les


         © UJF Grenoble, 2011                              Mentions légales