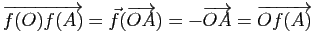
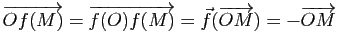
On pouvait naturellement aussi se contenter d'appliquer la proposition 32 au cas particulier ![]() .
.
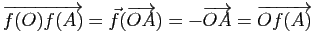
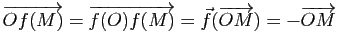
On pouvait naturellement aussi se contenter d'appliquer la proposition 32 au cas particulier ![]() .
.
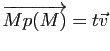 . Les coordonnées de
. Les coordonnées de
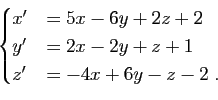
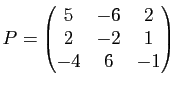
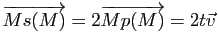 , où
, où
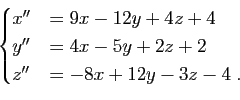
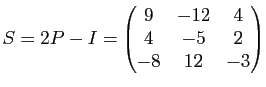
 |
 |
|
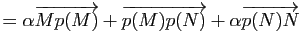 |
||
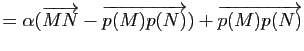 |
||
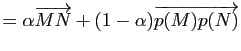 |
||
Il en résulte immédiatement par récurrence que la composée d'un nombre pair de symétries centrales est une translation.
Montrons par récurrence sur ![]() que
que
![]() pour
pour
![]() . On vient de voir que la propriété est vraie pour
. On vient de voir que la propriété est vraie pour ![]() . Si elle est vraie pour
. Si elle est vraie pour ![]() , comme
, comme ![]() est le milieu de
est le milieu de
![]() , on a
, on a
![]() , d'où
, d'où
![]() . De même
. De même
![]() .
.
L'application ![]() étant entièrement déterminée par les points
étant entièrement déterminée par les points
![]() , il en résulte que la donnée de ces points détermine
, il en résulte que la donnée de ces points détermine ![]() et, par récurrence, tous les points
et, par récurrence, tous les points ![]() , puisque
, puisque
![]() . L'application
. L'application ![]() est donc injective.
est donc injective.
Elle est également surjective, puisque, si ![]() sont les points précédemment définis,
sont les points précédemment définis, ![]() est le milieu de
est le milieu de
![]() pour tout
pour tout
![]() , et
, et ![]() le milieu de
le milieu de ![]() . L'application
. L'application ![]() est donc bijective.
est donc bijective.
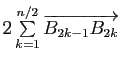 . Par ailleurs, la relation
. Par ailleurs, la relation
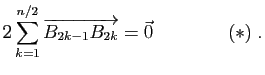
Soit
![]() un
un ![]() -uplet de points vérifiant la relation
-uplet de points vérifiant la relation ![]() et
et ![]() un point quelconque de
un point quelconque de ![]() . Définissons par récurrence des points
. Définissons par récurrence des points
![]() par
par
![]() pour
pour
![]() . Pour tout
. Pour tout
![]() ,
, ![]() est donc le milieu de
est donc le milieu de
![]() et il résulte de la relation
et il résulte de la relation ![]() que
que ![]() est l'identité, d'où
est l'identité, d'où
![]() .
. ![]() est donc le milieu de
est donc le milieu de ![]() et le
et le ![]() -uplet
-uplet
![]() est l'image par
est l'image par ![]() du
du ![]() -uplet
-uplet
![]() .
.
Il en résulte que l'image de ![]() est exactement l'ensemble des
est exactement l'ensemble des ![]() -uplets de points
-uplets de points
![]() vérifiant la relation
vérifiant la relation ![]() .
.
L'application ![]() n'est pas injective puisque le choix de
n'est pas injective puisque le choix de ![]() dans la construction précédente est arbitraire.
dans la construction précédente est arbitraire.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales