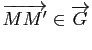 ). On peut donc définir une application
). On peut donc définir une application
Soit ![]() un espace affine,
un espace affine, ![]() un sous-espace affine de
un sous-espace affine de ![]() et
et
![]() un sous-espace vectoriel de
un sous-espace vectoriel de
![]() supplémentaire de
supplémentaire de
![]() . Il résulte de la proposition 9 que, pour tout point
. Il résulte de la proposition 9 que, pour tout point ![]() de
de ![]() , l'intersection
, l'intersection
![]() de
de ![]() et du sous-espace affine
et du sous-espace affine
![]() de direction
de direction
![]() passant par
passant par ![]() est constituée d'un point
est constituée d'un point ![]() et d'un seul (ce point
et d'un seul (ce point ![]() est l'unique point de
est l'unique point de ![]() vérifiant
vérifiant
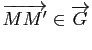 ). On peut donc définir une application
). On peut donc définir une application ![]() de
de ![]() dans lui-même par
dans lui-même par ![]() . Cette application est appelée projection sur
. Cette application est appelée projection sur ![]() parallèlement à
parallèlement à
![]() ou dans la direction
ou dans la direction
![]() .
.
Soit alors ![]() le symétrique de
le symétrique de ![]() par rapport à
par rapport à ![]() : on a donc
: on a donc
![]() . L'application
. L'application ![]() de
de ![]() dans lui-même qui à
dans lui-même qui à ![]() associe
associe ![]() est appelée symétrie par rapport à
est appelée symétrie par rapport à ![]() parallèlement à
parallèlement à
![]() ou dans la direction
ou dans la direction
![]() .
.
Plus généralement, pour tout réel ![]() , on définit l'affinité de base
, on définit l'affinité de base ![]() , de direction
, de direction
![]() et de rapport
et de rapport ![]() comme l'application qui au point
comme l'application qui au point ![]() associe le point
associe le point ![]() défini par
défini par
![]() . La projection et la symétrie sont donc des cas particuliers d'affinités correspondant respectivement à
. La projection et la symétrie sont donc des cas particuliers d'affinités correspondant respectivement à ![]() et
et ![]() .
.
Remarques :
Rappels d'algèbre linéaire : projections et symétries vectorielles.
Soit
![]() un espace vectoriel de dimension finie et
un espace vectoriel de dimension finie et
![]() et
et
![]() deux sous-espaces vectoriels supplémentaires de
deux sous-espaces vectoriels supplémentaires de
![]() . Tout vecteur
. Tout vecteur ![]() de
de
![]() s'écrit de manière unique sous la forme
s'écrit de manière unique sous la forme
![]() , avec
, avec
![]() (
(![]() ). Les deux applications
). Les deux applications
![]() et
et ![]() de
de
![]() dans lui-même définies par
dans lui-même définies par
![]() (
(![]() ) sont linéaires et vérifient les relations :
) sont linéaires et vérifient les relations :
Les deux applications ![]() et
et ![]() de
de
![]() dans lui-même définies par
dans lui-même définies par
![]() ,
,
![]() sont appelées symétrie par rapport à
sont appelées symétrie par rapport à
![]() (resp.
(resp.
![]() ) de direction (ou parallèlement à)
) de direction (ou parallèlement à)
![]() (resp.
(resp.
![]() ).
).
Elles sont linéaires, bijectives et vérifient les relations :
Réciproquement, si ![]() est une application linéaire de
est une application linéaire de
![]() dans lui-même vérifiant
dans lui-même vérifiant
![]() , les deux sous-espaces vectoriels
, les deux sous-espaces vectoriels
![]() et
et
![]() de
de
![]() sont supplémentaires et
sont supplémentaires et ![]() est la projection sur
est la projection sur
![]() parallèlement à
parallèlement à
![]() .
.
De même, si ![]() est une application linéaire de
est une application linéaire de
![]() dans lui-même vérifiant
dans lui-même vérifiant
![]() (on dit que
(on dit que ![]() est involutive),
est involutive), ![]() admet exactement les deux valeurs propres +1 et -1 (sauf si
admet exactement les deux valeurs propres +1 et -1 (sauf si
![]() , auquel cas elle n'admet qu'une valeur propre), et les noyaux des applications linéaires
, auquel cas elle n'admet qu'une valeur propre), et les noyaux des applications linéaires
![]() et
et
![]() (i.e. les sous-espaces propres de
(i.e. les sous-espaces propres de ![]() correspondant à ces deux valeurs propres) sont des sous-espaces vectoriels supplémentaires de
correspondant à ces deux valeurs propres) sont des sous-espaces vectoriels supplémentaires de
![]() ;
; ![]() est alors la symétrie par rapport au premier parallèlement au second.
est alors la symétrie par rapport au premier parallèlement au second.
Démonstration : Soient ![]() et
et ![]() deux points quelconques de
deux points quelconques de ![]() ,
, ![]() et
et ![]() leurs projetés sur
leurs projetés sur ![]() dans la direction
dans la direction
![]() ,
, ![]() et
et ![]() leurs symétriques par rapport à
leurs symétriques par rapport à ![]() dans la direction
dans la direction
![]() . Par la relation de Chasles, on a
. Par la relation de Chasles, on a
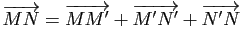 . Mais le vecteur
. Mais le vecteur
![]() appartient à
appartient à
![]() et le vecteur
et le vecteur
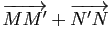 appartient à
appartient à
![]() comme somme de deux vecteurs de
comme somme de deux vecteurs de
![]() . On a donc
. On a donc
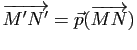 par définition de la projection vectorielle
par définition de la projection vectorielle ![]() , ce qui montre que
, ce qui montre que ![]() est affine de partie linéaire
est affine de partie linéaire ![]() .
.
De même l'égalité
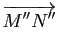 |
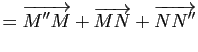 |
|
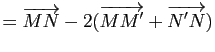 |
||
La démonstration pour l'affinité est analogue.![]()
Une projection, étant affine, conserve les rapports de mesures algébriques sur une même droite. La partie directe du théorème de Thalès ne fait que traduire cette propriété :
Soient ![]() ,
, ![]() ,
, ![]() trois droites parallèles distinctes d'un plan affine
trois droites parallèles distinctes d'un plan affine ![]() coupant deux droites
coupant deux droites ![]() et
et ![]() respectivement en
respectivement en ![]() ,
, ![]() ,
, ![]() et
et ![]() ,
, ![]() ,
, ![]() . Alors
. Alors
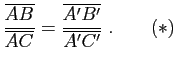
Réciproquement, soient ![]() ,
, ![]() ,
, ![]() trois droites distinctes d'un plan affine
trois droites distinctes d'un plan affine ![]() coupant deux droites
coupant deux droites ![]() et
et ![]() respectivement en
respectivement en ![]() ,
, ![]() ,
, ![]() et
et ![]() ,
, ![]() ,
, ![]() . On suppose
. On suppose ![]() et
et ![]() parallèles,
parallèles, ![]() et
et ![]() distincts et
distincts et
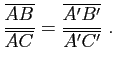
Démonstration : La partie directe du théorème résulte immédiatement du caractère affine de la projection ![]() sur
sur ![]() dans la direction commune des droites
dans la direction commune des droites ![]() ,
, ![]() ,
, ![]() : si
: si ![]() est un vecteur directeur de
est un vecteur directeur de ![]() et si les mesures algébriques sur
et si les mesures algébriques sur ![]() sont définies à partir de ce vecteur, les relations
sont définies à partir de ce vecteur, les relations
![]() ,
,
![]() impliquent
impliquent
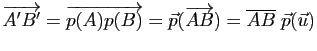 ,
,
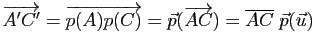 . En définissant les mesures algébriques sur
. En définissant les mesures algébriques sur ![]() en prenant
en prenant
![]() comme vecteur directeur (ce vecteur n'est pas nul, et on rappelle que les rapports de mesures algébriques sur une droite ne dépendent pas du choix du vecteur directeur), la relation
comme vecteur directeur (ce vecteur n'est pas nul, et on rappelle que les rapports de mesures algébriques sur une droite ne dépendent pas du choix du vecteur directeur), la relation ![]() en résulte immédiatement.
en résulte immédiatement.
Réciproquement, supposons la relation ![]() vérifiée. La parallèle à
vérifiée. La parallèle à ![]() menée par
menée par ![]() coupe la droite
coupe la droite ![]() en un point
en un point ![]() qui vérifie
qui vérifie
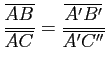 par la partie directe du théorème. Il en résulte
par la partie directe du théorème. Il en résulte
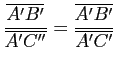 , d'où
, d'où
![]() et
et ![]() , ce qui montre que
, ce qui montre que ![]() est parallèle à
est parallèle à ![]() .
.![]()
La partie directe du théorème de Thalès ne faisant que traduire le caractère affine des projections, on peut énoncer un théorème analogue en toute dimension, en particulier dans l'espace de dimension 3 :
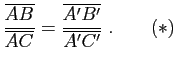
Mais le théorème de Thalès dans l'espace n'admet pas de réciproque analogue à celle du théorème de Thalès dans le plan : si on suppose les plans ![]() et
et ![]() parallèles et la relation
parallèles et la relation ![]() vérifiée, on ne peut en déduire que
vérifiée, on ne peut en déduire que ![]() est parallèle à
est parallèle à ![]() et
et ![]() . On a cependant :
. On a cependant :
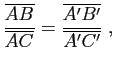
Démonstration : Si les droites ![]() et
et ![]() sont parallèles, les droites
sont parallèles, les droites ![]() et
et ![]() sont coplanaires et
sont coplanaires et ![]() est parallèle à
est parallèle à ![]() et
et ![]() par le théorème de Thalès dans le plan.
par le théorème de Thalès dans le plan.
Sinon, soient ![]() ,
, ![]() ,
, ![]() les plans passant respectivement par
les plans passant respectivement par ![]() ,
, ![]() ,
, ![]() de direction le plan vectoriel engendré par les vecteurs
de direction le plan vectoriel engendré par les vecteurs
![]() et
et
![]() . Ces trois plans sont parallèles et la droite
. Ces trois plans sont parallèles et la droite ![]() (resp.
(resp. ![]() ) est incluse dans
) est incluse dans ![]() (resp.
(resp. ![]() ) de sorte que
) de sorte que ![]() (resp.
(resp. ![]() ) coupe
) coupe ![]() en
en ![]() (resp.
(resp. ![]() ). Le plan
). Le plan ![]() coupe
coupe ![]() en un point
en un point ![]() qui vérifie
qui vérifie
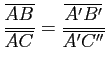 d'après le théorème direct. Il en résulte
d'après le théorème direct. Il en résulte
![]() , d'où
, d'où ![]() . La droite
. La droite ![]() est donc incluse dans
est donc incluse dans ![]() .
.![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales