- sinus hyperbolique l'application de
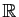 dans
dans
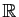 , définie par :
, définie par :
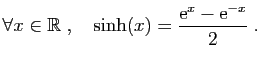
- cosinus hyperbolique l'application de
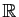 dans
dans
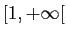 , définie par :
, définie par :
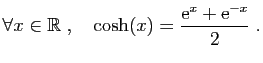
- tangente hyperbolique
l'application de
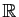 dans
dans ![$ ]-\!1,1[$](img292.gif) , définie par :
, définie par :
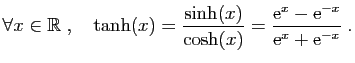
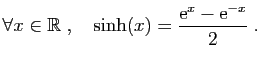
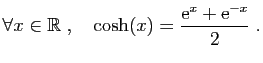
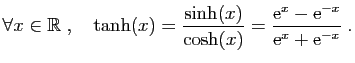
![\begin{displaymath}
\begin{array}{\vert c\vert c\vert c\vert c\vert}
\hline
\mul...
...{\mathrm{e}^{x}+\mathrm{e}^{-x}}{2}} [2ex]
\hline
\end{array}\end{displaymath}](img301.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales