Comme les fonctions circulaires, les fonctions hyperboliques ont
leurs réciproques, qui servent elles aussi aux calculs de
primitives (figure 9).
Figure 9:
Fonctions hyperboliques et leurs réciproques.
|
|
Elles sont moins importantes que leurs analogues circulaires,
car elles s'expriment de façon relativement simple
à l'aide du logarithme.
Démonstration : Résolvons l'équation
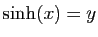 .
.
L'équation
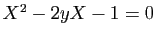 a deux racines réelles, dont seule
a deux racines réelles, dont seule
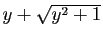 est positive. Donc
est positive. Donc
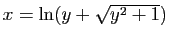 .
Résolvons l'équation
.
Résolvons l'équation
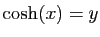 .
.
Pour
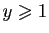 ,
l'équation
,
l'équation
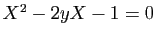 a deux racines réelles, dont seule
a deux racines réelles, dont seule
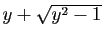 est supérieure à
est supérieure à 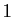 .
Donc
.
Donc
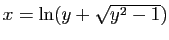 .
Résolvons l'équation
.
Résolvons l'équation
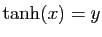 .
.
puisque
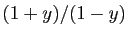 est strictement positif pour
est strictement positif pour
![$ y\in ]-\!1,1[ $](img328.gif) .
. Ici encore, le principal intérêt
réside dans les dérivées.
Ici encore, le principal intérêt
réside dans les dérivées.
Proposition 7
Les fonctions
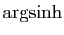 ,
,
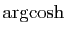 et
et
 sont dérivables sur leur domaine de définition.
sont dérivables sur leur domaine de définition.
-
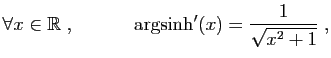
-
![$ \forall x\in ]1,+\infty[\;,\quad\! \arg\!\cosh'(x)=
\displaystyle{\frac{1}{\sqrt{x^2-1}}}\;,$](img333.gif)
-
![$ \forall x\in ]-\!1,1[\;,\quad \arg\!\tanh'(x)=
\displaystyle{\frac{1}{1-x^2}}\;.$](img334.gif)
Démonstration : On peut dériver directement l'expression en logarithme
ou bien appliquer la formule donnant la dérivée d'une fonction
réciproque.
 Définir une primitive de
Définir une primitive de 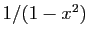 uniquement sur
uniquement sur ![$ ]-\!1,1[$](img292.gif) est un
tantinet réducteur, puisque la fonction :
est un
tantinet réducteur, puisque la fonction :
a pour dérivée
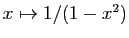 en tout point de
en tout point de
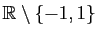 .
.
De même, définir une primitive de
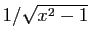 seulement sur
seulement sur
![$ ]1,+\infty[$](img343.gif) ne suffit pas, puisque la
fonction
ne suffit pas, puisque la
fonction
a pour dérivée
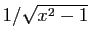 sur
sur
![$ ]-\!\infty,-1[$](img345.gif) et sur
et sur
![$ ]1,+\infty[$](img343.gif) .
C'est une raison suffisante pour vous conseiller de ne pas
trop surcharger votre mémoire vive avec les
fonctions hyperboliques réciproques.
.
C'est une raison suffisante pour vous conseiller de ne pas
trop surcharger votre mémoire vive avec les
fonctions hyperboliques réciproques.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
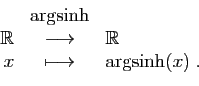
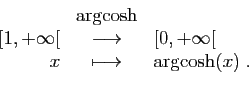
![\begin{displaymath}
\begin{array}{rcl}
&\arg\!\tanh&\\
{]-\!1,1[}&\longrightarrow&\mathbb{R}\\
x&\longmapsto&\arg\!\tanh(x)\;.
\end{array}\end{displaymath}](img308.gif)
![$ \forall x\in ]-\!1,1[\;,\quad \arg\!\tanh(x)=
\displaystyle{\frac{1}{2}\ln\left(\frac{1+x}{1-x}\right)}\;.$](img311.gif)
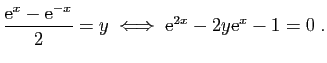
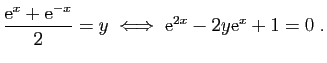
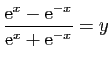
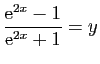
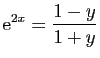
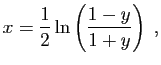
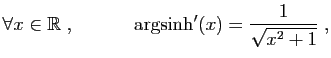
![$ \forall x\in ]1,+\infty[\;,\quad\! \arg\!\cosh'(x)=
\displaystyle{\frac{1}{\sqrt{x^2-1}}}\;,$](img333.gif)
![$ \forall x\in ]-\!1,1[\;,\quad \arg\!\tanh'(x)=
\displaystyle{\frac{1}{1-x^2}}\;.$](img334.gif)
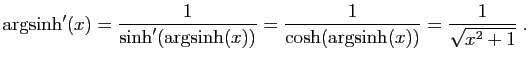
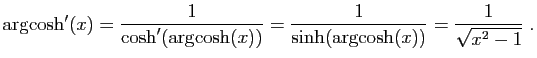
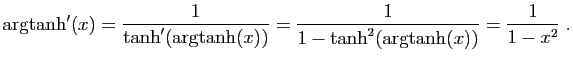
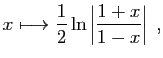
![]() seulement sur
seulement sur
![]() ne suffit pas, puisque la
fonction
ne suffit pas, puisque la
fonction
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales