Il se trouve que le facteur par lequel on multiplie la fonction
puissance de base 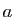 pour obtenir sa dérivée,
cette constante que nous avons sournoisement notée
pour obtenir sa dérivée,
cette constante que nous avons sournoisement notée
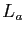 dans le théorème 1, est le logarithme
naturel, ou logarithme népérien de
dans le théorème 1, est le logarithme
naturel, ou logarithme népérien de 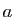 .
.
Définition 2
Soit 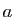 un réel strictement positif. On appelle
logarithme naturel de
un réel strictement positif. On appelle
logarithme naturel de
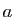 , et on note
, et on note 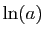 la dérivée en 0 de la fonction
la dérivée en 0 de la fonction
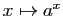 .
.
Théorème 2
- Pour tout
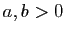 , on a :
, on a :
- Pour tout
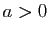 et
et
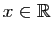 , on a :
, on a :
- La fonction
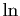 est strictement croissante, et :
est strictement croissante, et :
Démonstration : Nous reprenons la notation de la section précédente pour les
fonctions puissances : 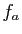 désigne la fonction
désigne la fonction
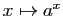 .
.
- Soient
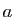 et
et 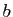 deux réels strictement
positifs. Considérons la fonction
deux réels strictement
positifs. Considérons la fonction  . On a :
. On a :
On calcule la dérivée de  en 0, en dérivant le
produit
en 0, en dérivant le
produit 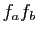 :
:
- Soit
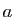 un réel strictement positif et soient
un réel strictement positif et soient
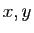 deux réels quelconques.
deux réels quelconques.
Fixons 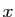 , dérivons par rapport à
, dérivons par rapport à 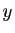 et prenons la dérivée en
0.
On obtient :
et prenons la dérivée en
0.
On obtient :
soit
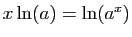 .
.
- Fixons
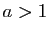 . D'après le point 2(b) du
théorème 1, la fonction
. D'après le point 2(b) du
théorème 1, la fonction
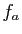 est strictement croissante.
On en déduit d'une part que
est strictement croissante.
On en déduit d'une part que 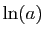 est strictement
positif, d'autre part que
est strictement
positif, d'autre part que 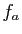 est
une bijection de
est
une bijection de
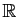 dans
dans
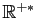 .
La relation
.
La relation
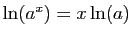 montre que la fonction réciproque de
montre que la fonction réciproque de 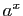 est la fonction qui à
est la fonction qui à
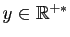 associe
associe
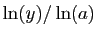 . Cette fonction est donc
strictement croissante et bijective de
. Cette fonction est donc
strictement croissante et bijective de
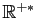 dans
dans
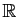 .
Les limites en
.
Les limites en 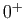 et
et 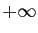 se déduisent aussi du
point 2(b) du théorème 1.
se déduisent aussi du
point 2(b) du théorème 1.
 Il nous reste à définir la fonction exponentielle, qui est la
réciproque du logarithme. D'après le point 3 du
théorème 2, il existe un réel unique, strictement
supérieur à 1, dont le logarithme vaut
Il nous reste à définir la fonction exponentielle, qui est la
réciproque du logarithme. D'après le point 3 du
théorème 2, il existe un réel unique, strictement
supérieur à 1, dont le logarithme vaut 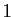 . On le note
. On le note
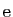 .
.
Définition 3
On appelle exponentielle, et on note 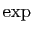 , la fonction qui à
, la fonction qui à
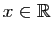 associe
associe
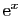 , où
, où
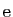 est l'unique réel
tel que
est l'unique réel
tel que
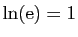 .
.
Ainsi, on pourra noter l'exponentielle de
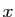 indifféremment
indifféremment
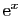 ou
ou 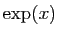 (la
seconde notation est préférable pour les grosses formules).
(la
seconde notation est préférable pour les grosses formules).
Théorème 3
L'exponentielle est la réciproque du logarithme. Les deux fonctions
sont strictement croissantes et dérivables.
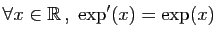
et
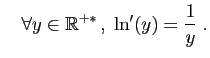
Démonstration : Puisque
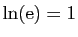 , on a
, on a
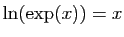 , par le point 2 du
théorème 2. La dérivée de l'exponentielle est
donnée par le point 4 du théorème 1. On
dérive le logarithme comme une fonction réciproque :
, par le point 2 du
théorème 2. La dérivée de l'exponentielle est
donnée par le point 4 du théorème 1. On
dérive le logarithme comme une fonction réciproque :
 La figure 2 montre les graphes des fonctions
La figure 2 montre les graphes des fonctions
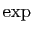 et
et 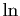 . Comme elles sont réciproques l'une de l'autre, leurs
graphes sont symétriques par rapport à la première bissectrice.
. Comme elles sont réciproques l'une de l'autre, leurs
graphes sont symétriques par rapport à la première bissectrice.
Figure:
Fonctions 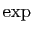 et
et 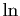 .
.
|
|
Comme nous l'avons vu dans la démonstration du théorème
2, le couple de fonctions réciproques
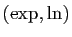 n'est qu'un cas particulier. Pour tout
n'est qu'un cas particulier. Pour tout 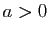 , la fonction puissance de
base
, la fonction puissance de
base 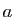 admet pour réciproque la fonction
admet pour réciproque la fonction
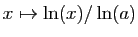 , que l'on appelle le logarithme en base
, que l'on appelle le logarithme en base 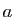 .
.
À part le logarithme en base
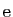 , qui est le logarithme naturel,
les deux bases les plus utilisées sont
, qui est le logarithme naturel,
les deux bases les plus utilisées sont 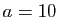 (logarithme décimal)
et
(logarithme décimal)
et 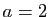 (logarithme binaire). Par définition, le logarithme en base
(logarithme binaire). Par définition, le logarithme en base
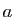 de
de 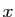 est le nombre
est le nombre 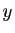 tel que
tel que 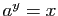 . Ainsi :
. Ainsi :
Il est facile de passer du logarithme en base 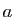 au logarithme
naturel, de même qu'il est facile de passer de l'exponentielle à
une autre fonction puissance, par la formule :
au logarithme
naturel, de même qu'il est facile de passer de l'exponentielle à
une autre fonction puissance, par la formule :
Nous terminons cette section par deux résultats d'approximation de
l'exponentielle. Le premier se redémontre facilement, le second est
absolument fondamental et doit être connu par c ur.
ur.
Théorème 4
Pour tout réel 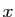 ,
,
Démonstration : Pour la première limite, écrivons :
Or  et
et 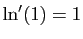 . On en déduit :
. On en déduit :
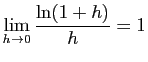
et donc,

Comme la fonction 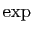 est continue, ceci entraîne bien :
est continue, ceci entraîne bien :
Nous démontrons la seconde formule à partir de la première, en
utilisant la formule du binôme de Newton.
Supposons d'abord
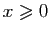 .
Fixons
.
Fixons
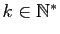 : pour tout
: pour tout
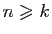 :
:
Or pour 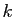 fixé :
fixé :
En passant à la limite en 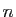 , on en déduit que pour tout
, on en déduit que pour tout 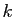 :
:
Dans cette inégalité, le membre de droite est le terme général
d'une suite croissante et majorée (par
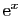 ),
donc il converge, et :
),
donc il converge, et :
D'autre part, observons que pour tout
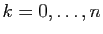 ,
,
Donc :
Puisque nous savons que le membre de droite converge, on en déduit
par passage à la limite :
D'où le résultat, pour 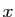 positif ou nul.
positif ou nul.
Pour 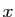 négatif,
l'astuce consiste à faire disparaître les termes impairs en
prenant la demi-somme de
négatif,
l'astuce consiste à faire disparaître les termes impairs en
prenant la demi-somme de
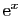 et
et
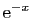 (nous verrons plus loin que cette demi-somme est le cosinus
hyperbolique de
(nous verrons plus loin que cette demi-somme est le cosinus
hyperbolique de 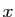 ).
).
Le même raisonnement que précédemment montre que :
Par linéarité de la limite, on en déduit alors que :
 Les résultats d'approximation permettent de calculer les
exponentielles avec une précision arbitraire. Voici le nombre
Les résultats d'approximation permettent de calculer les
exponentielles avec une précision arbitraire. Voici le nombre
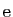 arrondi à la cinquantième décimale.
arrondi à la cinquantième décimale.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
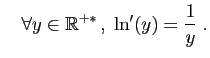
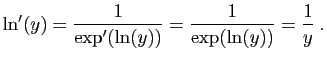
![]() n'est qu'un cas particulier. Pour tout
n'est qu'un cas particulier. Pour tout ![]() , la fonction puissance de
base
, la fonction puissance de
base ![]() admet pour réciproque la fonction
admet pour réciproque la fonction
![]() , que l'on appelle le logarithme en base
, que l'on appelle le logarithme en base ![]() .
.
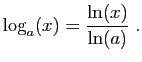
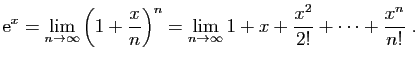
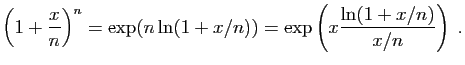
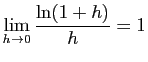 et donc,
et donc, 
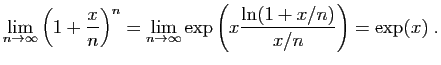
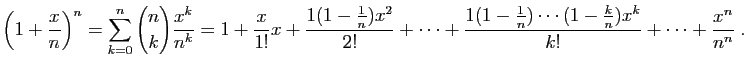
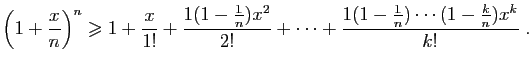
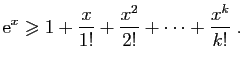
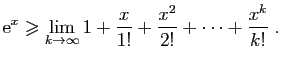
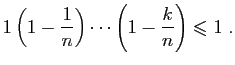
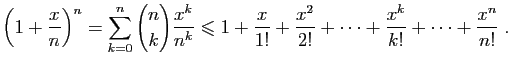
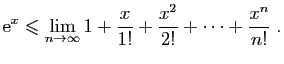
![]() négatif,
l'astuce consiste à faire disparaître les termes impairs en
prenant la demi-somme de
négatif,
l'astuce consiste à faire disparaître les termes impairs en
prenant la demi-somme de
![]() et
et
![]() (nous verrons plus loin que cette demi-somme est le cosinus
hyperbolique de
(nous verrons plus loin que cette demi-somme est le cosinus
hyperbolique de ![]() ).
).
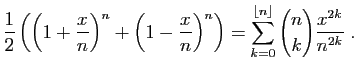

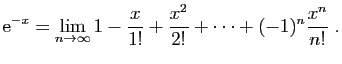
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales