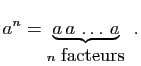
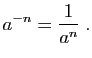
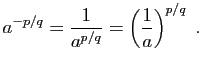
si ![]() , alors
, alors
![]() ,
,
si ![]() , alors
, alors
![]() .
.
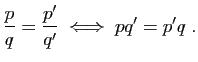
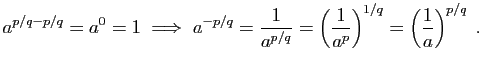
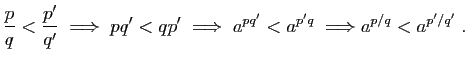
Passons au cas ![]() .
Soient
.
Soient ![]() et
et ![]() deux réels tels que
deux réels tels que ![]() . Il existe un rationnel
. Il existe un rationnel
![]() tel que
tel que ![]() .
Soient
.
Soient ![]() et
et ![]() les suites
des approximations décimales par défaut de
les suites
des approximations décimales par défaut de ![]() et
et ![]() . Il existe
un certain rang
. Il existe
un certain rang ![]() tel que pour tout
tel que pour tout
![]() ,
,
![]() . Pour
. Pour ![]() , les suites
, les suites ![]() et
et ![]() sont
croissantes. et
sont
croissantes. et
![]() . Par
passage à la limite,
. Par
passage à la limite,
![]() .
Donc
.
Donc
![]() est strictement croissante pour
est strictement croissante pour ![]() .
Toute fonction croissante admet une limite en
.
Toute fonction croissante admet une limite en ![]() et en
et en
![]() . Pour identifier ces limites, il suffit de considérer une
suite tendant vers
. Pour identifier ces limites, il suffit de considérer une
suite tendant vers ![]() et une suite tendant vers
et une suite tendant vers ![]() , par
exemple les suites d'entiers
, par
exemple les suites d'entiers ![]() et
et ![]() . Or :
. Or :
Pour ![]() , inutile de refaire les démonstrations : il suffit
d'utiliser la formule
, inutile de refaire les démonstrations : il suffit
d'utiliser la formule
![]() , conséquence de
(1).
, conséquence de
(1).
Nous allons d'abord montrer que pour tout
![]() :
:
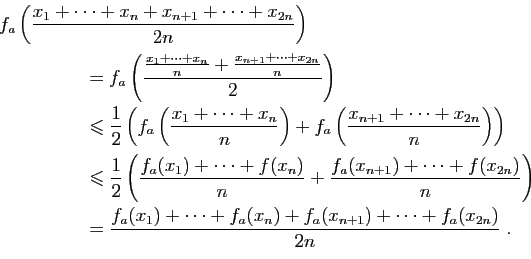
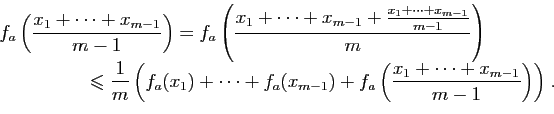
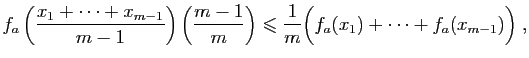
Soient ![]() et
et ![]() deux entiers positifs tels que
deux entiers positifs tels que ![]() , et
, et ![]() deux
réels tels que
deux
réels tels que ![]() . Appliquons (3) pour
. Appliquons (3) pour ![]() ,
,
![]() , et
, et
![]() . On obtient :
. On obtient :
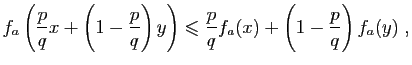
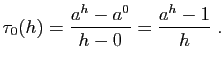
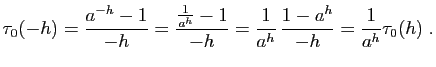
Pour en déduire la dérivabilité en un
point ![]() quelconque de
quelconque de
![]() , il suffit d'appliquer une fois de plus
la propriété (1) :
, il suffit d'appliquer une fois de plus
la propriété (1) :
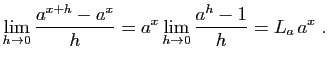
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales