Les définitions et résultats de cette section sont énoncés
pour la dimension 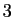 , afin de ne pas compliquer les notations. Ils se
généralisent facilement en dimension quelconque.
, afin de ne pas compliquer les notations. Ils se
généralisent facilement en dimension quelconque.
Soit
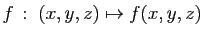 une
application de
une
application de
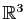 dans
dans
 . Etant donné un point de
coordonnées
. Etant donné un point de
coordonnées 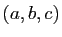 dans
dans
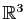 , on
définit
, on
définit  applications partielles en
applications partielles en 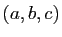 .
.
Nous souhaitons dériver ces trois applications. Or on ne peut
dériver une fonction de
 dans
dans
 que si elle est définie
au voisinage du point où on souhaite la dériver,
c'est-à-dire sur un intervalle ouvert contenant ce point. Ceci nous
amène à introduire la définition suivante.
que si elle est définie
au voisinage du point où on souhaite la dériver,
c'est-à-dire sur un intervalle ouvert contenant ce point. Ceci nous
amène à introduire la définition suivante.
Le cube de centre 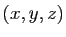 et de côté
et de côté 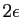 doit être vu
comme un voisinage de
doit être vu
comme un voisinage de 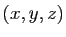 . Dorénavant les fonctions que
nous considérons sont définies sur un domaine ouvert
. Dorénavant les fonctions que
nous considérons sont définies sur un domaine ouvert 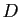 inclus
dans
inclus
dans
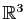 .
Si les
applications partielles sont dérivables, leurs dérivées
s'appellent les dérivées partielles de
.
Si les
applications partielles sont dérivables, leurs dérivées
s'appellent les dérivées partielles de  en
en 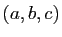 .
.
Pour calculer la dérivée partielle par rapport à 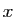 , il suffit
de dériver en
, il suffit
de dériver en 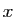 l'expression de
l'expression de  , en traitant les autres
variables comme des constantes paramétriques.
, en traitant les autres
variables comme des constantes paramétriques.
Supposons par exemple que  soit l'application qui à
soit l'application qui à 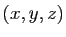 associe la surface du parallélépipède dont les longueurs
d'arêtes sont
associe la surface du parallélépipède dont les longueurs
d'arêtes sont 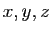 .
.
Voici ses trois dérivées partielles.
Nous éviterons systématiquement les cas pathologiques en supposant
que les dérivées partielles sont des fonctions continues.
Définition 4
Soit  une application définie sur un domaine ouvert
une application définie sur un domaine ouvert 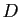 de
de
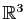 , à valeurs dans
, à valeurs dans
 .
On dit que
.
On dit que  est continûment différentiable sur
est continûment différentiable sur
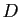 si les dérivées partielles
si les dérivées partielles
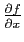 ,
,
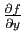 , et
, et
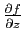 ,
vues comme des fonctions de
,
vues comme des fonctions de
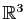 dans
dans
 sont continues en tout
point de
sont continues en tout
point de 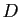 .
.
Si elles sont continues, les dérivées partielles permettent
d'approcher la fonction par une application linéaire au voisinage
d'un point. Le résultat qui suit est l'analogue pour les fonctions
de deux variables d'un développement limité d'ordre 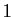 .
.
Ce théorème dit que les variations de la fonction  autour du
point
autour du
point 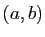 peuvent être approchées par une application
linéaire, la différentielle
de
peuvent être approchées par une application
linéaire, la différentielle
de  .
.
La différentielle peut être vue comme l'application qui à un vecteur
associe son produit scalaire par le vecteur des dérivées partielles,
qu'on appelle le gradient de  au point
au point 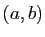 ,
et que l'on note
,
et que l'on note
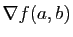 (prononcez :
«nabla»).
En physique, on interprète
(prononcez :
«nabla»).
En physique, on interprète 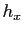 et
et 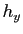 comme de petites
variations des variables
comme de petites
variations des variables 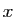 et
et 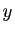 , et on les note plutôt
, et on les note plutôt
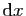 et
et
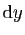 . Si on note
. Si on note
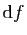 la différentielle de
la différentielle de  , ceci
justifie l'écriture abrégée suivante.
, ceci
justifie l'écriture abrégée suivante.
Le théorème
2 donne une approximation de 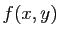 sous la forme :
sous la forme :
La surface d'équation
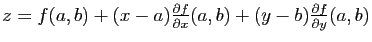 est celle du plan tangent
à la surface
est celle du plan tangent
à la surface 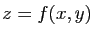 au point
au point
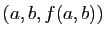 (cf.
figure 5). Pour rappeler cette
interprétation géométrique, la différentielle de
(cf.
figure 5). Pour rappeler cette
interprétation géométrique, la différentielle de  au point
au point
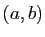 porte aussi le nom d'application linéaire tangente.
porte aussi le nom d'application linéaire tangente.
Figure 5:
Plan tangent à une surface en un point.
|
|
Une application de
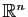 dans
dans
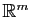 est continûment
différentiable si ses
est continûment
différentiable si ses 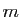 applications coordonnées le sont, au sens
de la définition 4. La différentielle en un point de
applications coordonnées le sont, au sens
de la définition 4. La différentielle en un point de
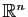 est une application linéaire de
est une application linéaire de
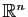 dans
dans
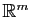 . Sa
matrice est la matrice jacobienne. Ici encore nous donnons la
définition en dimension réduite pour des raisons de clarté.
. Sa
matrice est la matrice jacobienne. Ici encore nous donnons la
définition en dimension réduite pour des raisons de clarté.
On ne distinguera pas en général la matrice jacobienne au point
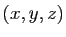 de l'application de
de l'application de
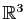 dans l'ensemble des matrices qui
à
dans l'ensemble des matrices qui
à 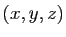 associe cette matrice jacobienne. Nous reprenons les
exemples de la section précédente, en donnant pour chacun la
matrice jacobienne.
Surface d'un rectangle en fonction de sa longueur et sa largeur :
associe cette matrice jacobienne. Nous reprenons les
exemples de la section précédente, en donnant pour chacun la
matrice jacobienne.
Surface d'un rectangle en fonction de sa longueur et sa largeur :
Surface d'un parallélépipède en fonction de ses trois dimensions :
Surface et volume
d'un parallélépipède en fonction de ses trois dimensions :
Coordonnées polaires d'un point du plan :
Coordonnées cylindriques d'un point de l'espace :
Coordonnées sphériques d'un point de l'espace :
Pour le calcul des différentielles, on est souvent amené à
utiliser la règle de dérivation selon laquelle
la différentielle d'une fonction composée est la composée
des différentielles.
Voici un exemple. Considérons l'application  , de
, de
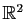 dans
dans
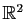 , qui aux coordonnées polaires d'un point du plan associe ses
coordonnées cartésiennes.
, qui aux coordonnées polaires d'un point du plan associe ses
coordonnées cartésiennes.
Considérons maintenant la fonction 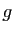 , de
, de
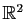 dans
dans
 qui
à
qui
à 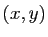 associe
associe 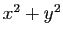 .
.
La matrice jacobienne de 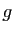 au point
au point
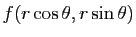 est
donc
est
donc
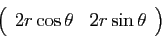 .
Le produit des deux est :
.
Le produit des deux est :
Effectivement, la composée 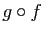 est la fonction de
est la fonction de
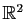 dans
dans
 qui à
qui à
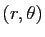 associe
associe 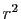 . En pratique, on calcule
rarement les différentielles sous forme matricielle. On écrira
plutôt :
. En pratique, on calcule
rarement les différentielles sous forme matricielle. On écrira
plutôt :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() une
application de
une
application de
![]() dans
dans
![]() . Etant donné un point de
coordonnées
. Etant donné un point de
coordonnées ![]() dans
dans
![]() , on
définit
, on
définit ![]() applications partielles en
applications partielles en ![]() .
.
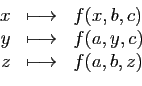
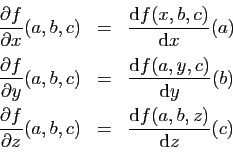
![]() soit l'application qui à
soit l'application qui à ![]() associe la surface du parallélépipède dont les longueurs
d'arêtes sont
associe la surface du parallélépipède dont les longueurs
d'arêtes sont ![]() .
.
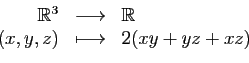
![\begin{displaymath}
\begin{array}{rcl}
\displaystyle{\frac{\partial f}{\partial ...
...partial z}(a,b,c)}&=&
\displaystyle{2(a+b)} [2ex]
\end{array}\end{displaymath}](img65.gif)
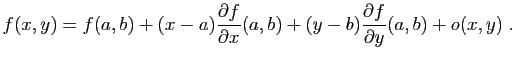
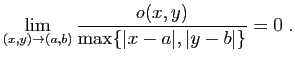
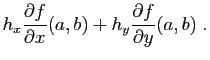
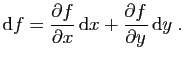
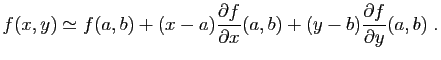
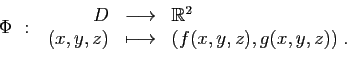
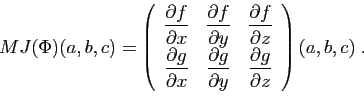
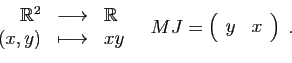
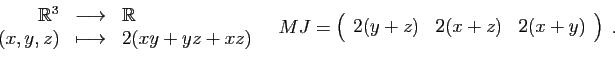
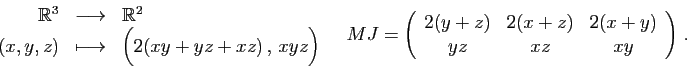
![\begin{displaymath}
\begin{array}{rcl}
\mathbb{R}^{+*}\times ]0,2\pi[&\longright...
...a&-r\sin\theta\\
\sin\theta&r\cos\theta
\end{array}\right)\;.
\end{displaymath}](img96.gif)
![\begin{displaymath}
\begin{array}{rcl}
\mathbb{R}^{+*}\times ]0,2\pi[\times \mat...
...\
\sin\theta&r\cos\theta& 0\\
0&0& 1
\end{array}\right)\;.
\end{displaymath}](img97.gif)
![\begin{displaymath}
\begin{array}{rcl}
\mathbb{R}^{+*}\times ]0,2\pi[\times ]-\f...
...os\theta ,\;y=r\cos\phi\sin\theta
,\;z=r\sin\phi
\end{array}\end{displaymath}](img98.gif)
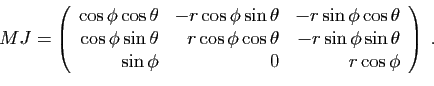
![\begin{displaymath}
f :\;\left\{\begin{array}{rcl}
\mathbb{R}^{+*}\times ]0,2\p...
...a&-r\sin\theta\\
\sin\theta&r\cos\theta
\end{array}\right)\;.
\end{displaymath}](img105.gif)
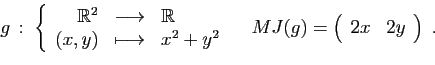
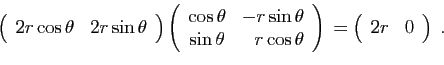
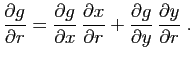
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales