-
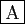
- L'application
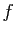 est définie sur
est définie sur
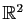 .
.
-
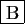
- L'application
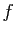 est continue sur
est continue sur
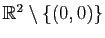 .
.
-
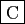
- L'application
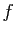 est continue sur
est continue sur
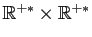 .
.
-
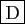
- L'application
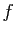 est continûment différentiable sur
est continûment différentiable sur
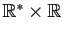 .
.
-
- L'application
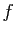 est continûment différentiable sur
est continûment différentiable sur
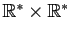 .
.
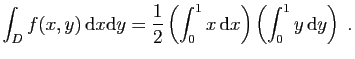
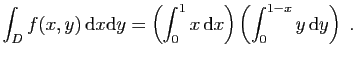
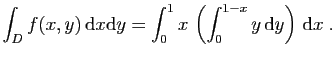
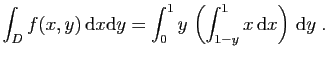
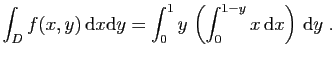
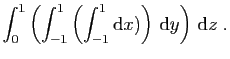
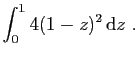
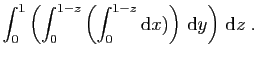
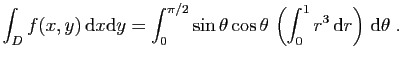
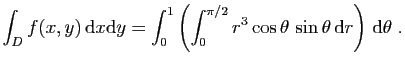
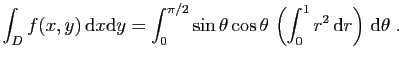
![$ \displaystyle{
\int_D f(x,y) \mathrm{d}x\mathrm{d}y =
\Big[-\frac{\cos 2\theta }{4}\Big]_0^{\pi}\times
\Big[ \frac{r^4}{4}\Big]_{-1}^1\;.
}$](img553.gif)
![$ \displaystyle{
\int_D f(x,y) \mathrm{d}x\mathrm{d}y =
\Big[-\frac{\cos 2\theta }{4}\Big]_0^{\pi/2}\times
\Big[ \frac{r^4}{4}\Big]_0^1\;.
}$](img554.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales