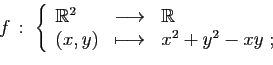
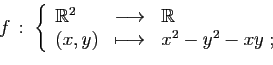
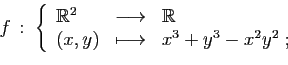
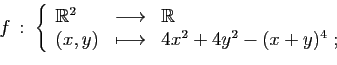
- Calculer le gradient de
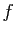 .
.
- Donner l'équation du plan tangent à la surface d'équation
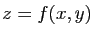 ,
aux points
,
aux points 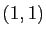 ,
, 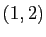 ,
, 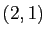 .
.
- Déterminer les points critiques de
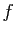 .
.
- Calculer la matrice hessienne de
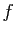 .
.
- Soit
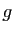 l'application de
l'application de
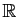 dans
dans
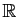 qui à
qui à 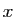 associe
associe
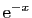 .
Calculer directement, puis en utilisant les dérivées partielles de
.
Calculer directement, puis en utilisant les dérivées partielles de 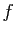 ,
la dérivée de l'application
de
,
la dérivée de l'application
de
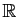 dans
dans
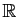 qui à
qui à 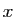 associe
associe 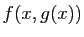 .
.
- Pour chacun des points critiques de
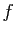 , donner les
conclusions tirées de l'examen de la matrice hessienne.
, donner les
conclusions tirées de l'examen de la matrice hessienne.
- Pour chacun des points critiques de
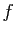 , dire s'il
s'agit ou non d'un extremum global de
, dire s'il
s'agit ou non d'un extremum global de 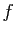 .
.
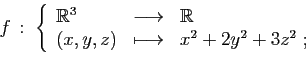
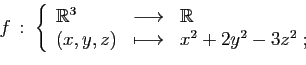
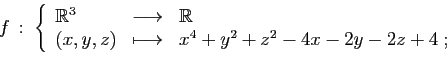
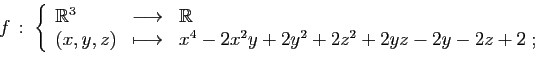
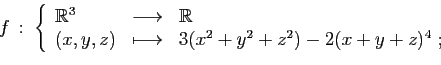
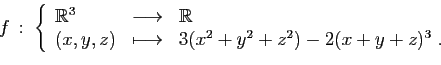
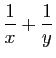
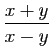
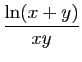
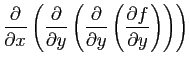
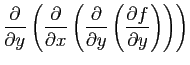
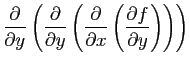
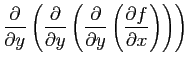
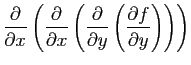
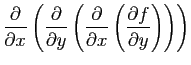
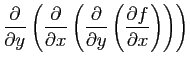
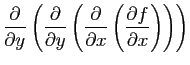
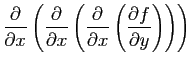
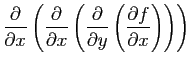
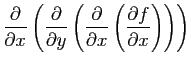
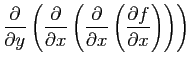
![\begin{displaymath}
\Phi(x,y)=(u,v) :\;
\left\{
\begin{array}{lcl}
u&=&\displaystyle{x+y} [2ex]
v&=&\displaystyle{x-y}\;.
\end{array}\right.
\end{displaymath}](img490.gif)
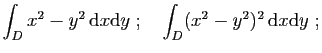
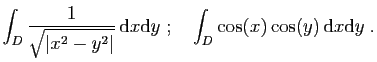
![\begin{displaymath}
\Phi(x,y)=(u,v) :\;
\left\{
\begin{array}{lcl}
u&=&\display...
...y^2}} [2ex]
v&=&\displaystyle{x^2+y^2}\;.
\end{array}\right.
\end{displaymath}](img494.gif)
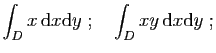
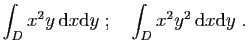
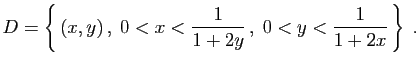
![\begin{displaymath}
\Phi(x,y)=(u,v) :\;
\left\{
\begin{array}{lcl}
u&=&\display...
...]
v&=&\displaystyle{\frac{y(1+x)}{1-xy}}\;.
\end{array}\right.
\end{displaymath}](img498.gif)
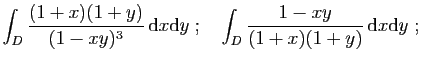
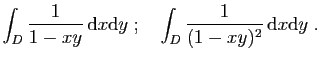
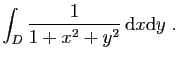
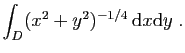
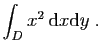
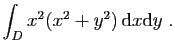
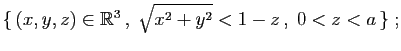
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales