Section : Cours
Avant : Fonctions holomorphes
Après : Propriétés élémentaires des fonctions holomorphes


Théorie de Cauchy locale

Le but de cette section est de prouver une première version de la formule de Cauchy, qui est un des éléments clé de la théorie des fonctions holomorphes. Nous en déduirons l'équivalence entre dérivabilité complexe et analyticité pour les fonctions d'une variable complexe. Cette équivalence est spécifique au domaine complexe, en effet toute fonction analytique d'une variable réelle est bien sûr dérivable, mais il existe des fonctions dérivables d'une variable réelle et même de classe $ \mathcal{C}^\infty$ qui ne sont pas analytiques comme par exemple la fonction définie sur $ \mathbb{R}$ par $ f(x)=\mathrm{e}^{-\frac{1}{x^2}}$ pour $ x\neq 0$ et $ f(0)=0$.

Intégrales curvilignes

Définition 3   Soit $ U$ un ouvert de $ \mathbb{R}^2$, on appelle chemin de classe $ \mathcal {C}^1$ ( ou arc paramétré de classe $ \mathcal {C}^1$) de $ U$ une application $ \gamma : [a,b]\to U$ de classe $ \mathcal {C}^1$. On supposera toujours que $ a<b$, l'origine de $ \gamma$ est le point $ \gamma(a)$, l'extrémité de $ \gamma$ est le point $ \gamma(b)$, le chemin est fermé si $ \gamma(a)=\gamma(b)$. L'image de $ \gamma$ (c'est-à-dire l'ensemble des points $ \gamma(t), t\in [a,b])$ sera notée $ \Gamma$.

Figure 2: Chemin de classe $ \mathcal {C}^1$.
\includegraphics[width=6cm]{cheminc1}

Exemples

1) L'application $ \gamma : [0,2\pi]\to \mathbb{C}$ définie par $ \gamma(t)=\mathrm{e}^{\mathrm{i}t}$ est un chemin fermé et $ \Gamma=\{z\in\mathbb{C} \vert \vert z\vert=1\}$

2) L'application $ \widetilde{\gamma} : [0,3\pi]\to \mathbb{C}$ définie par $ \gamma(t)=\mathrm{e}^{\mathrm{i}t}$ n'est pas un chemin fermé, son origine est $ 1$ et son extrémité est $ -1$, et $ \widetilde{\Gamma}=\Gamma$ mais $ \widetilde{\gamma}\neq\gamma$.

Définition 4   Deux chemins $ ([a,b],\gamma)$ et $ ([c,d],\delta)$ sont dits équivalents s'il existe une application $ \varphi : [a,b]\to[c,d]$ vérifiant les conditions suivantes :

i) $ \varphi$ est bijective, croissante et de classe $ \mathcal {C}^1$ ainsi que $ \varphi^{-1}$

ii) $ \gamma=\delta\circ\varphi$.

Définition 5   Soit $ ([a,b],\gamma)$ un chemin de classe $ \mathcal {C}^1$ et $ f$ une fonction continue sur $ \Gamma$. L'intégrale de $ f$ sur $ \gamma$, notée $ \int_\gamma f(z) \mathrm{d}z$, est définie par

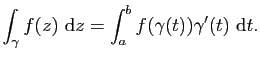
$\displaystyle \int_\gamma f(z) \mathrm{d}z=\int_a^b f(\gamma(t))\gamma'(t) \mathrm{d}t.$

Proposition 3   Si $ ([a,b],\gamma)$ et $ ([c,d],\delta)$ sont deux chemins équivalents et si $ f$ est une fonction continue sur $ \Gamma$, on a

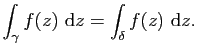
$\displaystyle \int_\gamma f(z) \mathrm{d}z=\int_\delta f(z) \mathrm{d}z.$

Démonstration : La formule du changement de variable dans les intégrales donne

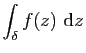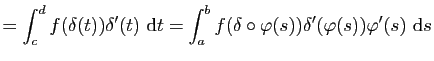$\displaystyle \int_\delta f(z) \mathrm{d}z$ $\displaystyle =\int_c^d f(\delta(t))\delta'(t) \mathrm{d}t=\int_a^b f(\delta\circ\varphi(s))\delta'(\varphi(s))\varphi'(s) \mathrm{d}s$    
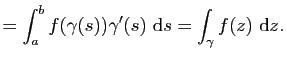  $\displaystyle =\int_a^b f(\gamma(s))\gamma'(s) \mathrm{d}s=\int_\gamma f(z) \mathrm{d}z.$    

$ \square$ Remarque. Si $ ([a,b],\gamma)$ est un chemin de classe $ \mathcal {C}^1$, la longueur $ L$ de $ \gamma$ est par définition, si $ \gamma(t)=(x(t),y(t))$,

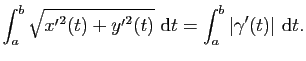
$\displaystyle \int_a^b \sqrt{{x'}^2(t)+{y'}^2(t)} \mathrm{d}t=\int_a^b \vert\gamma'(t)\vert \mathrm{d}t.$

Si $ f$ est une fonction continue sur $ \Gamma$, alors

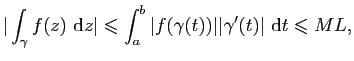
$\displaystyle \vert\int_\gamma f(z) \mathrm{d}z\vert\leqslant \int_a^b \vert f(\gamma(t))\vert\vert\gamma'(t)\vert \mathrm{d}t\leqslant ML,$

où $ L$ est la longueur de $ \gamma$ et $ M=\sup_{z\in\Gamma} \vert f(z)\vert$.

Définition 6   Soit $ U$ un ouvert de $ \mathbb{R}^2$, un chemin $ \gamma$ sera dit de classe $ \mathcal {C}^1$ par morceaux dans $ U$ s'il existe une subdivision de $ [a,b]$ par des points $ a_0=a<a_1<\dots<a_j<\dots<a_k=b$ telle que les restrictions $ \gamma_j$ de $ \gamma$ à chaque intervalle $ [a_{j-1},a_j]$, $ j=1,\dots,k$, soient de classe $ \mathcal {C}^1$ et vérifient $ \gamma_j(a_j)=\gamma_{j+1}(a_j)$, $ j=0,\dots,k-1$ ($ \gamma$ est constitué de $ k$ chemins de classe $ \mathcal {C}^1$ mis bout à bout). Si $ f$ est une fonction continue sur $ \Gamma$, on pose

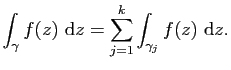
$\displaystyle \int_\gamma f(z) \mathrm{d}z=\sum_{j=1}^k \int_{\gamma_j} f(z) \mathrm{d}z.$

Figure 3: Chemin fermé, de classe $ \mathcal {C}^1$ par morceaux.
\includegraphics[width=6cm]{cheminferme}

Exemples


$ \bullet$ Si $ ([a,b],\gamma)$ est un chemin de classe $ \mathcal {C}^1$ par morceaux dans $ U$ et $ f$ une fonction continue sur $ U$ telle que $ f=F'$, où $ F$ est une fonction holomorphe sur $ U$, on a

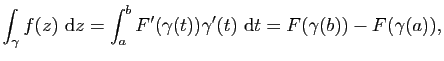
$\displaystyle \int_\gamma f(z) \mathrm{d}z=\int_a^b F'(\gamma(t))\gamma'(t) \mathrm{d}t=F(\gamma(b))-F(\gamma(a)),$

en particulier si $ \gamma$ est un chemin fermé $ \int_\gamma f(z) \mathrm{d}z=0$.

Par exemple pour $ n\in\mathbb{Z}\setminus\{-1\}$, $ f(z)=(z-\omega)^n$ avec $ \omega\notin\Gamma$ vérifie $ f=F'$ pour $ F(z)=\frac{1}{n+1}(z-\omega)^{n+1}$ et par conséquent $ \int_\gamma (z-\omega)^n \mathrm{d}z=0$ pour tout chemin fermé $ \gamma$ tel que $ \omega\notin\Gamma$.


$ \bullet$ Soient $ \gamma : [0,2\pi]\to \mathbb{C}$ défini par $ \gamma(t)=\mathrm{e}^{\mathrm{i}t}$ et $ \omega\in\mathbb{C}$ tel que $ \vert\omega\vert<1$, on pose $ f_\omega(z)=\frac{1}{z-\omega}$. Nous allons calculer la valeur de $ \int_\gamma f_\omega(z) \mathrm{d}z=\int_0^{2\pi}\frac{\mathrm{i}\mathrm{e}^{\mathrm{i}t}}{\mathrm{e}^{\mathrm{i}t}-\omega} \mathrm{d}t$. Posons $ g(s)=\int_0^{2\pi}\frac{\mathrm{i}\mathrm{e}^{\mathrm{i}t}}{\mathrm{e}^{\mathrm{i}t}-s\omega} \mathrm{d}t$, $ s\in [0,1]$. La fonction $ \varphi(s,t)=\frac{\mathrm{i}\mathrm{e}^{\mathrm{i}t}}{\mathrm{e}^{\mathrm{i}t}-s\omega}$ est continue sur $ [0,1]\times[0,2\pi]$. La fonction $ \frac{\partial\varphi}{\partial s}(s,t)=\frac{\mathrm{i}\omega \mathrm{e}^{\mathrm{i}t}}{(\mathrm{e}^{\mathrm{i}t}-s\omega)^2}$ est aussi continue sur $ [0,1]\times[0,2\pi]$. La théorie des intégrales dépendant d'un paramètre implique, puisque nous intégrons sur un segment, que $ g$ est une fonction de classe $ \mathcal {C}^1$ sur $ [0,1]$. De plus $ g(0)=2\mathrm{i}\pi$ et $ g(1)=\int_\gamma f_\omega(z) \mathrm{d}z$, mais

$\displaystyle g'(s)=\int_0^{2\pi}\frac{\mathrm{i}\omega \mathrm{e}^{\mathrm{i}t... ...mathrm{e}^{\mathrm{i}t}-s\omega)})}_{\Phi(t)} \mathrm{d}t=\Phi(0)-\Phi(2\pi)=0,$

donc $ g$ est constante sur $ [0,1]$ et $ g(1)=g(0)$, soit

$\displaystyle \int_\gamma f_\omega(z) \mathrm{d}z=\int_\gamma \frac{\mathrm{d}z}{z-\omega}= 2\mathrm{i}\pi.$

Définition 7   Si $ \gamma$ est un chemin fermé de classe $ \mathcal {C}^1$ par morceaux et $ z$ un point du complémentaire de l'image $ \Gamma$ de $ \gamma$, on appelle indice du chemin $ \gamma$ par rapport à $ z$ le nombre

$\displaystyle \mathrm{Ind}_\gamma(z)=\frac{1}{2\mathrm{i}\pi}\int_\gamma \frac{1}{w-z} \mathrm{d}w.$

Figure 4: Indice d'un chemin fermé.
\includegraphics[width=6cm]{indice}

Proposition 4   Soit $ [a,b],\gamma$ un chemin fermé de classe $ \mathcal {C}^1$ par morceaux. L'indice du chemin $ \gamma$ par rapport à un point définit une fonction $ \mathrm{Ind}_\gamma$ sur $ \mathbb{C}\setminus\Gamma$ à valeurs dans $ \mathbb{Z}$, constante sur chaque composante connexe de $ \mathbb{C}\setminus\Gamma$ et nulle sur la composante connexe non bornée de $ \mathbb{C}\setminus\Gamma$.

Démonstration : Sans perte de généralité on peut supposer que le chemin $ \gamma$ est de classe $ \mathcal {C}^1$. Pour $ z\in\mathbb{C}\setminus\Gamma$ on considère la fonction $ \varphi$ définie sur $ [a,b]$ par

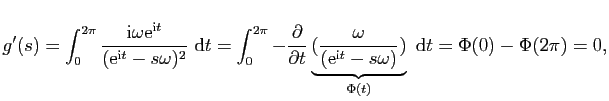
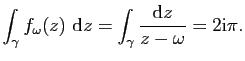
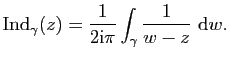
$\displaystyle \varphi(s)=\exp \left[\int_a^s\frac{\gamma'(t)}{\gamma(t)-z} \mathrm{d}t\right].$

Nous allons montrer que la fonction $ \psi(s)=\frac{\varphi(s)}{\gamma(s)-z}$ est constante sur l'intervalle $ [a,b]$. Puisque le chemin $ \gamma$ est de classe $ \mathcal {C}^1$, la fonction $ \psi$ est aussi de classe $ \mathcal {C}^1$ sur l'intervalle $ [a,b]$ et il suffit donc de prouver que $ \psi'(s)=0$ pour tout $ s\in [a,b]$. Mais

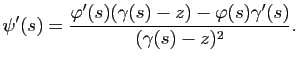
$\displaystyle \psi'(s)=\frac{\varphi'(s)(\gamma(s)-z)-\varphi(s)\gamma'(s)}{(\gamma(s)-z)^2}.$

et $ \varphi'(s)=\frac{\gamma'(s)}{\gamma(s)-z}\varphi(s)$, par conséquent $ \psi'(s)=0$. Nous obtenons donc $ \psi(a)=\psi(b)$ et, puisque $ \gamma(a)=\gamma(b)$ (le chemin $ \gamma$ est fermé), cela donne $ \varphi(b)=\varphi(a)=1$, soit $ \mathrm{Ind}_\gamma(z)\in\mathbb{Z}$ par définition de $ \varphi$.

La fonction $ \mathrm{Ind}_\gamma(z)=\frac{1}{2\mathrm{i}\pi}\int_a^b\frac{\gamma'(t)}{\gamma(t)-z} \mathrm{d}t$ est définie comme une intégrale sur le segment $ [a,b]$ dépendant du paramètre $ z$. La fonction $ (t,z)\mapsto \frac{\gamma'(t)}{\gamma(t)-z}$ est continue sur $ [a,b]\times \mathbb{C}\setminus\Gamma$ donc $ \mathrm{Ind}_\gamma$ est continue, de plus elle est à valeurs entières et par conséquent constante sur chaque composante connexe de $ \mathbb{C}\setminus\Gamma$.

Soit $ R_0$ tel que $ \Gamma$ soit contenu dans le disque $ D(0,R_0)$. Si $ \vert z\vert>R_0+r$, alors $ \vert\gamma(t)-z\vert>r$ pour tout $ t\in[a,b]$ et

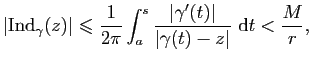
$\displaystyle \vert\mathrm{Ind}_\gamma(z)\vert\leqslant \frac{1}{2\pi}\int_a^s\frac{\vert\gamma'(t)\vert}{\vert\gamma(t)-z\vert} \mathrm{d}t<\frac{M}{r},$

avec $ M=\frac{b-a}{2\pi}\sup_{t\in[a,b]}\vert\gamma'(t)\vert$. On en déduit que $ \lim_{\vert z\vert\to\infty}\vert\mathrm{Ind}_\gamma(z)\vert=0$ et, puisque $ \mathrm{Ind}_\gamma(z)$ est à valeurs entières, $ \mathrm{Ind}_\gamma(z)=0$ sur la composante connexe non bornée de $ \mathbb{C}\setminus\Gamma$.$ \square$ Formule de Cauchy pour les disques

Nous présentons ici un cas particulier de la formule générale de Cauchy. Ce cas particulier est suffisant pour prouver les propriétés élémentaires des fonctions holomorphes qui seront développées dans la section 1.3.

Théorème 2 (Formule de Cauchy)   Soient $ U$ un ouvert de $ \mathbb{C}$, $ a$ un point de $ U$ et $ r>0$ tel que le disque ouvert $ D(a,r)$ de centre $ a$ et de rayon $ r$ soit contenu dans $ U$. On note $ \gamma$ le chemin $ \gamma(t)=a+r\mathrm{e}^{\mathrm{i}t}$, $ t\in [0,2\pi]$. Si $ f$ est une fonction holomorphe sur $ U$ alors pour tout $ z\in D(a,r)$ on a

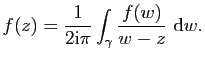$\displaystyle f(z)=\frac{1}{2\mathrm{i}\pi}\int_\gamma\frac{f(w)}{w-z} \mathrm{d}w.$ (1)

Démonstration : Quitte à translater et dilater, i.e. remplacer $ f$ par $ \widetilde{f}(z)=f(a+rz)$, on peut se ramener au cas où $ a=0$ et $ r=1$. On doit montrer que

$\displaystyle f(z)=\frac{1}{2\pi}\int_0^{2\pi}\frac{f(\mathrm{e}^{\mathrm{i}t})\mathrm{e}^{\mathrm{i} t}}{\mathrm{e}^{\mathrm{i}t}-z} \mathrm{d}t$   si$\displaystyle \quad \vert z\vert<1.$ (2)

Posons $ g(s)=\frac{1}{2\pi}\int_0^{2\pi}\left(\frac{f(z+s(\mathrm{e}^{\mathrm{i}t}-z))\mathrm{e}^{\mathrm{i}t}}{\mathrm{e}^{\mathrm{i}t}-z}\right) \mathrm{d}t$ pour $ s\in [0,1]$. On a $ \vert z+s(\mathrm{e}^{\mathrm{i}t}-z)\vert=\vert z(1-s)+s\mathrm{e}^{\mathrm{i}t}\vert<1-s+s=1$, donc $ f(z+s(\mathrm{e}^{\mathrm{i}t}-z))$ est bien définie si $ 0\leqslant s\leqslant 1$. De plus $ g(1)$ coincide avec le second membre de (2) et

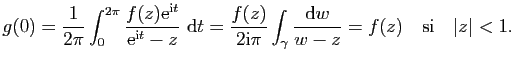
$\displaystyle g(0)=\frac{1}{2\pi}\int_0^{2\pi}\frac{f(z)\mathrm{e}^{\mathrm{i}t... ...\pi}\int_\gamma\frac{\mathrm{d}w}{w-z}=f(z)\quad \mbox{si}\quad \vert z\vert<1.$

On va prouver que la fonction $ g$ est constante sur $ [0,1]$. La fonction $ \varphi(s,t)=\frac{f(z+s(\mathrm{e}^{\mathrm{i}t}-z))\mathrm{e}^{\mathrm{i}t}}{\mathrm{e}^{\mathrm{i}t}-z}$ est continue sur $ [0,1]\times[0,2\pi]$. La fonction $ \frac{\partial\varphi}{\partial s}(s,t)=f'(z+s(\mathrm{e}^{\mathrm{i}t}-z))\mathrm{e}^{\mathrm{i}t}$ est aussi continue sur $ [0,1]\times[0,2\pi]$. De plus

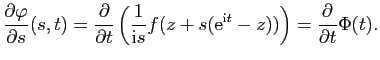
$\displaystyle \frac{\partial\varphi}{\partial s}(s,t)=\frac{\partial}{\partial ... ...s}f(z+s(\mathrm{e}^{\mathrm{i}t}-z))\right)=\frac{\partial}{\partial t}\Phi(t).$

La théorie des intégrales dépendant d'un paramètre implique, puisque nous intégrons sur un segment, que $ g$ est une fonction de classe $ \mathcal {C}^1$ sur $ [0,1]$ et que

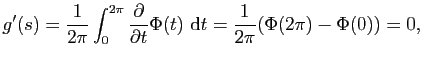
$\displaystyle g'(s)=\frac{1}{2\pi}\int_0^{2\pi}\frac{\partial}{\partial t}\Phi(t) \mathrm{d}t=\frac{1}{2\pi}(\Phi(2\pi)-\Phi(0))=0,$

donc la fonction $ g$ est constante sur $ [0,1]$ et $ g(1)=g(0)=f(z)$, soit

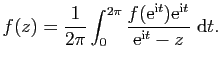
$\displaystyle f(z)=\frac{1}{2\pi}\int_0^{2\pi}\frac{f(\mathrm{e}^{\mathrm{i}t})\mathrm{e}^{\mathrm{i}t}}{\mathrm{e}^{\mathrm{i}t}-z} \mathrm{d}t.$

$ \square$

Corollaire 1 (Analyticité des fonctions holomorphes)   Soit $ U$ un ouvert de $ \mathbb{C}$. Toute fonction holomorphe dans $ U$ est analytique dans $ U$. Si $ a\in U$ et si $ d(a,\mathbb{C}\setminus U)$ désigne la distance de $ a$ au complémentaire de $ U$, le rayon de convergence de la série de Taylor de $ f$ au point $ a$ est supérieur ou égal à $ d(a,\mathbb{C}\setminus U)$.

De plus si le disque fermé $ \overline{D(a,r)}$ est contenu dans $ U$, on a

$\displaystyle f^{(n)}(a)=\frac{n!}{2\mathrm{i}\pi}\int_{\mathcal{C}(a,r)}\frac{f(w)}{(w-a)^{n+1}} \mathrm{d}w,$ (3)

où $ \mathcal{C}(a,r)$ désigne le chemin défini sur $ [0,2\pi]$ par $ t\mapsto a+r\mathrm{e}^{\mathrm{i}t}$.

Démonstration : Soit $ a\in U$ et $ D=D(a,d(a,\mathbb{C}\setminus U))$, $ D$ est le plus grand disque de centre $ a$ contenu dans $ U$. Soit $ r$ tel que $ 0<r<d(a,\mathbb{C}\setminus U)$ et $ z\in D(a,r)$, alors la formule de Cauchy nous donne

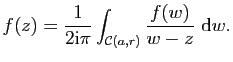
$\displaystyle f(z)=\frac{1}{2\mathrm{i}\pi}\int_{\mathcal{C}(a,r)}\frac{f(w)}{w-z} \mathrm{d}w.$

Si $ z\in D(a,r)$ et si $ w$ vérifie $ \vert w-a\vert=r$, on a $ \vert z-a\vert<\vert w-a\vert$ et

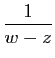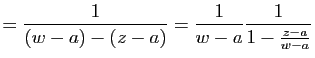$\displaystyle \frac{1}{w-z}$ $\displaystyle =\frac{1}{(w-a)-(z-a)}=\frac{1}{w-a}\frac{1}{1-\frac{z-a}{w-a}}$    
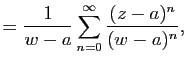  $\displaystyle =\frac{1}{w-a}\sum_{n=0}^\infty \frac{(z-a)^n}{(w-a)^n},$    

d'où

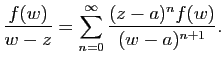
$\displaystyle \frac{f(w)}{w-z}=\sum_{n=0}^\infty \frac{(z-a)^n f(w)}{(w-a)^{n+1}}.$

Cette série de fonctions de $ w$ est normalement convergente donc uniformément convergente sur $ \mathcal{C}(a,r)$ (on utilise ici la même notation pour le chemin et son image) puisque son terme général est majoré par

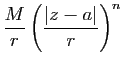$\displaystyle \frac{M}{r}\left(\frac{\vert z-a\vert}{r}\right)^n$   avec$\displaystyle \quad M=\sup_{w\in\mathcal{C}(a,r)} \vert f(w)\vert.$

On peut donc intégrer terme à terme et on trouve

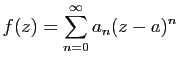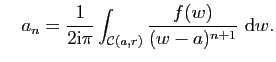
$\displaystyle f(z)=\sum_{n=0}^\infty a_n(z-a)^n$   avec$\displaystyle \quad a_n=\frac{1}{2\mathrm{i}\pi}\int_{\mathcal{C}(a,r)}\frac{f(w)}{(w-a)^{n+1}} \mathrm{d}w.$

La fonction $ f$ est donc analytique dans $ U$ et la série de Taylor en $ a$ de $ f$ coïncide avec $ f$ au moins sur le plus grand disque ouvert de centre $ a$ contenu dans $ U$ puisque, si $ z$ est dans ce disque, on peut intercaler $ r$ entre $ \vert z-a\vert$ et $ d(a,\mathbb{C}\setminus U)$.$ \square$ Remarque. Remarquons que dans le cas des fonctions analytiques réelles le disque de convergence de la série de Taylor en un point n'est pas nécessairement le plus grand disque contenu dans le domaine de définition de la fonction. Il suffit de considérer la fonction $ f(x)=\frac{1}{1+x^2}$ qui est analytique sur $ \mathbb{R}$ et dont le rayon de convergence de la série de Taylor en 0 vaut $ 1$.

Corollaire 2   Soit $ U$ un ouvert de $ \mathbb{C}$. Si $ f\in\mathcal{H}(U)$ alors $ f'\in\mathcal{H}(U)$ et $ f$ est indéfiniment dérivable.

Démonstration : D'après le Corollaire 1, la fonction $ f$ est analytique et donc de classe $ \mathcal{C}^\infty$ et sa dérivée est aussi analytique et par conséquent holomorphe.$ \square$

Propriétés. Les fonctions holomorphes étant analytiques elles vérifient :

$ \bullet$ le principe du prolongement analytique;

$ \bullet$ le principe des zéros isolés.


Résumé.

    $ f$ holomorphe sur $ U$    
Séries entières
(rien de nouveau)
$ \Uparrow$   $ \Downarrow$
Formule de Cauchy
(idée nouvelle)
    $ f$ analytique sur $ U$    

Section : Cours
Avant : Fonctions holomorphes
Après : Propriétés élémentaires des fonctions holomorphes


         © UJF Grenoble, 2011                              Mentions légales