Exercice 2
Pour chacun des couples
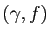 suivants, calculer
suivants, calculer
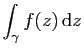 .
.
-
![\begin{displaymath}\displaystyle{
\begin{array}{rcl}
&\gamma& [0.1ex]
[0,\pi]&...
...ghtarrow&\mathbb{C}\\
z&
\longmapsto& \frac{1}{z}
\end{array}}\end{displaymath}](img1162.gif)
-
![\begin{displaymath}\displaystyle{
\begin{array}{rcl}
&\gamma& [0.1ex]
[0,1]&\l...
...&\longrightarrow&\mathbb{C}\\
z&
\longmapsto& z^2
\end{array}}\end{displaymath}](img1163.gif)
-
![\begin{displaymath}\displaystyle{
\begin{array}{rcl}
&\gamma& [0.1ex]
\mathbb{...
...b{C}\\
z&
\longmapsto& \mathrm{e}^{-\vert z\vert}
\end{array}}\end{displaymath}](img1164.gif)
-
![\begin{displaymath}\displaystyle{
\begin{array}{rcl}
&\gamma& [0.1ex]
\mathbb{...
...rrow&\mathbb{C}\\
z&
\longmapsto& \mathrm{e}^{-z}
\end{array}}\end{displaymath}](img1165.gif)
Exercice 3
Pour chacun des chemins fermés suivants :
- Décrire l'image
 de
de  .
.
- Donner les valeurs de
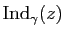 , pour tout
, pour tout
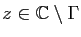 .
.
- Pour chacune des fonctions suivantes :
Calculer
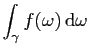
Exercice 4
Soit 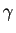 un chemin fermé dans
un chemin fermé dans
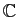 de classe
de classe
 par
morceaux. Soient
par
morceaux. Soient 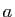 et
et 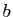 deux points distincts de
deux points distincts de
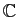 non situés
sur l'image de
non situés
sur l'image de 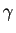 .
.
- Calculer l'intégrale
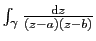 en
fonction de l'indice de
en
fonction de l'indice de 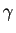 par rapport à
par rapport à 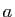 et par rapport à
et par rapport à 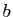 .
.
- Que peut-on dire de la valeur de l'intégrale lorsqu'il existe un
chemin
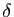 passant par
passant par 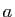 et
et 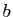 et ne rencontrant pas
et ne rencontrant pas
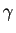 ?
?
- En déduire la valeur de l'intégrale
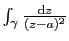 .
.
- Calculer directement l'intégrale
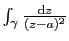 .
.
Exercice 6
Soit 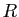 un réel strictement positif et
un réel strictement positif et
le secteur de centre 0, de rayon 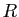 et d'angle
et d'angle
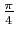 , on
note
, on
note 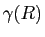 le chemin fermé de classe
le chemin fermé de classe
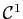 par morceaux défini par
le bord orienté du secteur
par morceaux défini par
le bord orienté du secteur 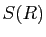 .
.
En intégrant la fonction
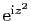 sur le chemin
sur le chemin 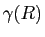 montrer
que
montrer
que
et que
existent et calculer leurs valeurs.
Exercice 17
Soient 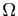 et
et 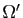 deux ouverts connexes de
deux ouverts connexes de
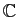 et
et
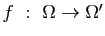 une application holomorphe telle que pour tout
compact
une application holomorphe telle que pour tout
compact 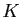 de
de 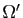 ,
, 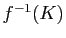 soit un compact de
soit un compact de 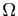 . On
dira dans ce cas que
. On
dira dans ce cas que  est propre.
est propre.
- Montrer par un raisonnement purement topologique simple que
 est
une application fermée, c'est-à-dire si
est
une application fermée, c'est-à-dire si 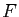 est un fermé de l'ouvert
est un fermé de l'ouvert
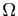 ,
, 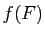 est fermé dans
est fermé dans 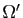 .
.
- Montrer que
 est surjective, i.e.
est surjective, i.e.
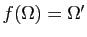 .
.
- En considérant l'application
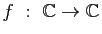 définie par un
polynôme non constant, en déduire une nouvelle démonstration du
théorème de d'Alembert.
définie par un
polynôme non constant, en déduire une nouvelle démonstration du
théorème de d'Alembert.
Exercice 24
On rappelle que les racines de 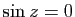 sont réelles. Soit
sont réelles. Soit  la fonction méromorphe définie par
la fonction méromorphe définie par
- Déterminer les points singuliers de
 .
.
- Calculer le résidu de
 en chacun de ses pôles.
en chacun de ses pôles.
- Pour tout entier naturel
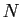 , soit
, soit 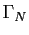 le bord orienté
positivement du carré
de sommets
le bord orienté
positivement du carré
de sommets
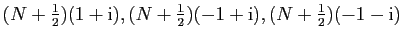 et
et
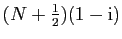 .
.
Montrer que si
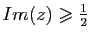 on a
on a
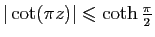 et que si
et que si
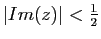 , alors
pour tout
, alors
pour tout
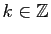
En déduire la limite quand 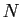 tend vers l'infini de
tend vers l'infini de
- Calculer la somme de la série
Exercice 27
Soient 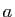 et
et 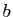 deux réels strictement positifs.
On considère la fonction qui à
deux réels strictement positifs.
On considère la fonction qui à 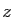 associe :
associe :
- Montrer que la fonction
 est méromorphe, calculer ses 4
pôles, et donner le résidu de
est méromorphe, calculer ses 4
pôles, et donner le résidu de  en chacun de ces pôles.
en chacun de ces pôles.
- Soit
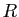 un réel positif.
On note
un réel positif.
On note 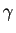 le chemin qui à
le chemin qui à
![$ t\in [0,\pi]$](img1103.gif) associe
associe
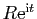 .
Démontrer que
.
Démontrer que
- On suppose
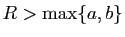 .
En appliquant le théorème des résidus, calculer
.
En appliquant le théorème des résidus, calculer
- Déduire de ce qui précède que
Exercice 28
On considère la fonction qui à 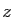 associe :
associe :
- Montrer que la fonction
 est méromorphe, calculer ses 4
pôles, et donner le résidu de
est méromorphe, calculer ses 4
pôles, et donner le résidu de  en chacun de ces pôles.
en chacun de ces pôles.
- Soit
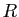 un réel positif.
On note
un réel positif.
On note 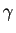 le chemin qui à
le chemin qui à
![$ t\in [0,\pi]$](img1103.gif) associe
associe
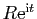 .
Démontrer que
.
Démontrer que
- On suppose
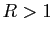 .
En appliquant le théorème des résidus, calculer
.
En appliquant le théorème des résidus, calculer
- Déduire de ce qui précède que
Exercice 30
Soit
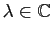 tel que
tel que
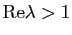 . Montrer que
l'équation
. Montrer que
l'équation
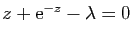 a exactement une solution dans le
demi-plan
a exactement une solution dans le
demi-plan
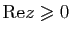 . On pourra considérer un demi disque de
centre 0 et de rayon
. On pourra considérer un demi disque de
centre 0 et de rayon 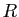 assez grand.
assez grand.
Exercice 31
Soit  un ouvert connexe borné de
un ouvert connexe borné de
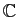 , contenant l'origine et
, contenant l'origine et
 une application holomorphe de
une application holomorphe de  dans lui-même telle que
dans lui-même telle que
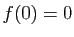 . On va montrer que
. On va montrer que  est un automorphisme de
est un automorphisme de  si et
seulement si
si et
seulement si 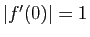 .
.
- Montrer qu'il existe des constantes
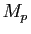 ,
,
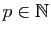 , telles que
pour toute fonction
, telles que
pour toute fonction 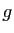 holomorphe dans
holomorphe dans  vérifiant
vérifiant
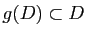 ,
on ait :
,
on ait :
- Soit
 une fonction holomorphe dans
une fonction holomorphe dans  vérifiant
vérifiant
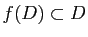 et
et 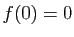 .
.
- On définit les fonctions
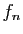 par
par 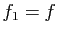 et la
relation de récurrence
et la
relation de récurrence
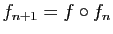 si
si
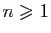 . Montrer que
. Montrer que
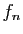 est holomorphe dans
est holomorphe dans  et calculer
et calculer 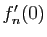 en fonction de
en fonction de
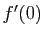 .
.
- En déduire que
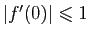 .
.
- Montrer que, si
 est un automorphisme de
est un automorphisme de  ,
, 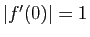 .
.
- Montrer que, si
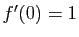 ,
, 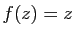 pour tout
pour tout 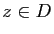 . (On
raisonnera par l'absurde en supposant que le développement de
. (On
raisonnera par l'absurde en supposant que le développement de  en
série entière à l'origine s'écrit :
en
série entière à l'origine s'écrit :
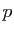 étant un entier strictement supérieur à
étant un entier strictement supérieur à 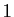 , et on calculera le
coefficient de
, et on calculera le
coefficient de 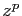 dans le développement de
dans le développement de  .)
.)
- On suppose qu'il existe
 ,
,  , tel que
, tel que
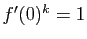 . Montrer que
. Montrer que  est un automorphisme de
est un automorphisme de  .
.
- On munit l'espace
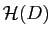 des
fonctions holomorphes dans
des
fonctions holomorphes dans  de la topologie de la convergence
uniforme sur tout compact de
de la topologie de la convergence
uniforme sur tout compact de  .
.
- Montrer que l'ensemble des fonctions fonctions
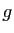 holomorphes dans
holomorphes dans  vérifiant
vérifiant
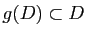 et
et 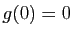 est une partie compacte de
est une partie compacte de
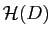 .
.
- On suppose que
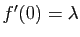 ,
,
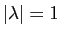 et que
l'ensemble
et que
l'ensemble
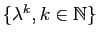 est dense l'ensemble
est dense l'ensemble
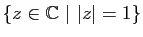 . Montrer qu'il existe une sous-suite de la suite
. Montrer qu'il existe une sous-suite de la suite
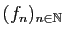 qui converge uniformément sur tout compact de
qui converge uniformément sur tout compact de  vers l'identité de
vers l'identité de  .
.
- Montrer que pour toute suite
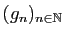 de fonctions
holomorphes sur
de fonctions
holomorphes sur  qui converge vers une fonction
qui converge vers une fonction 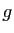 uniformément
sur tout compact de
uniformément
sur tout compact de  , si
, si 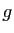 prend la valeur
prend la valeur 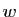 et n'est pas la
fonction constante égale à
et n'est pas la
fonction constante égale à 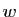 , alors pour
, alors pour 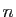 assez grand la fonction
assez grand la fonction
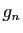 prend la valeur
prend la valeur 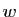 .
.
- On rappelle que tout sous-groupe multiplicatif du groupe des
nombres complexes de module
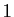 est fini ou dense.
est fini ou dense.
Déduire de ce qui précède que, si 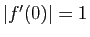 ,
,  est une application
injective et surjective de
est une application
injective et surjective de  sur lui-même.
sur lui-même.
Exercice 32
Calculer le développement en série de Laurent de  en
en 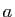 dans les
cas suivants.
dans les
cas suivants.
-
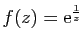 en
en 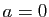
-
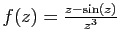 en
en 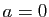
-
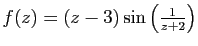 en
en 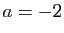
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
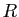 (éventuellement infini) de
la série entière
(éventuellement infini) de
la série entière
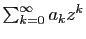 où
où 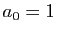 et
et
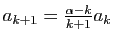 pour
pour
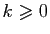 (on discutera suivant
les valeurs de
(on discutera suivant
les valeurs de 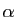 ). On note
). On note 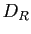 le disque de convergence de
cette série et, si
le disque de convergence de
cette série et, si 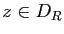 , on note
, on note
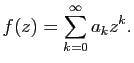
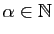 . Déterminer
. Déterminer  .
.
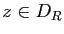 , comparer
, comparer
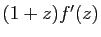 et
et 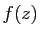 .
.
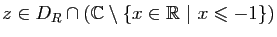 , comparer
, comparer
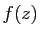 et
et
 . Ici
. Ici 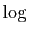 désigne la détermination principale du logarithme complexe.
désigne la détermination principale du logarithme complexe.
 se prolonge de manière unique en une fonction
analytique dans
se prolonge de manière unique en une fonction
analytique dans
 . Calculer la
valeur de cette fonction en
. Calculer la
valeur de cette fonction en
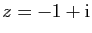 si
si
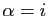 . Existe-t-il des
valeurs de
. Existe-t-il des
valeurs de 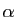 (
(
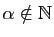 ) pour lesquelles
) pour lesquelles  se prolonge
en une fonction analytique dans
se prolonge
en une fonction analytique dans
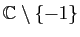 ?
?
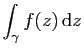
![\begin{displaymath}\displaystyle{
\begin{array}{rcl}
&\gamma& [0.1ex]
[0,\pi]&...
...ghtarrow&\mathbb{C}\\
z&
\longmapsto& \frac{1}{z}
\end{array}}\end{displaymath}](img1162.gif)
![\begin{displaymath}\displaystyle{
\begin{array}{rcl}
&\gamma& [0.1ex]
[0,1]&\l...
...&\longrightarrow&\mathbb{C}\\
z&
\longmapsto& z^2
\end{array}}\end{displaymath}](img1163.gif)
![\begin{displaymath}\displaystyle{
\begin{array}{rcl}
&\gamma& [0.1ex]
\mathbb{...
...b{C}\\
z&
\longmapsto& \mathrm{e}^{-\vert z\vert}
\end{array}}\end{displaymath}](img1164.gif)
![\begin{displaymath}\displaystyle{
\begin{array}{rcl}
&\gamma& [0.1ex]
\mathbb{...
...rrow&\mathbb{C}\\
z&
\longmapsto& \mathrm{e}^{-z}
\end{array}}\end{displaymath}](img1165.gif)
![\begin{displaymath}
\begin{array}{rcl}
&\gamma& [0.1ex]
[0,2\pi]&\longrightarr...
...thbb{C}\\
t&
\longmapsto& \mathrm{e}^{\mathrm{i}t}
\end{array}\end{displaymath}](img1166.gif)
![\begin{displaymath}
\begin{array}{rcl}
&\gamma& [0.1ex]
[0,4]&\longrightarrow...
...x{si}&3\leqslant t\leqslant 4\\
\end{array}\right.
\end{array}\end{displaymath}](img1167.gif)
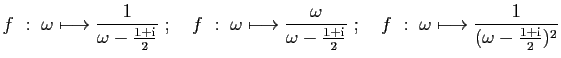
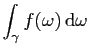
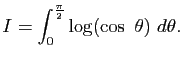
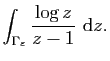
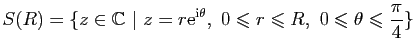
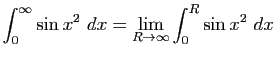
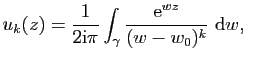 pour
pour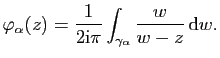
![% latex2html id marker 27255
\includegraphics[width=8cm]{exodemiplan}](img1223.gif)
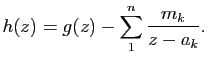
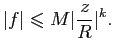
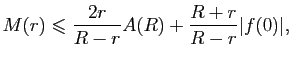
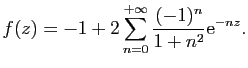
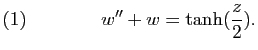
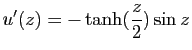 et
et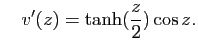
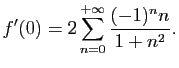
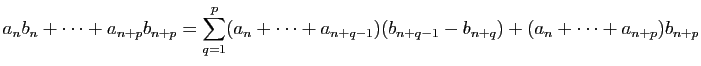
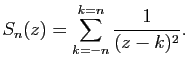
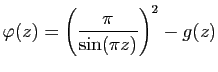
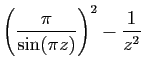
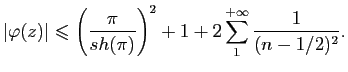
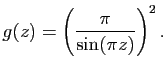
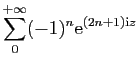
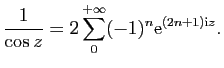
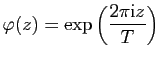
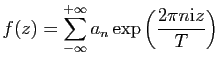
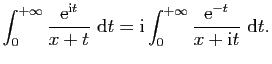
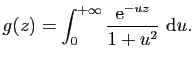
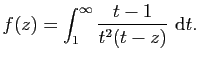
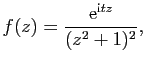
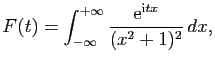
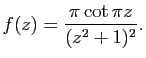
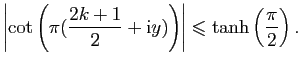
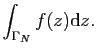
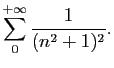
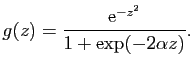
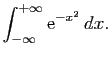
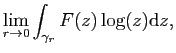 et
et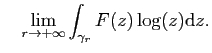
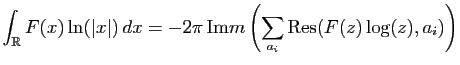
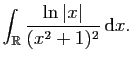
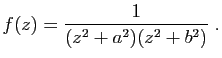
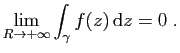
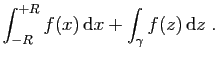
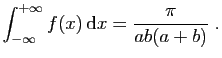
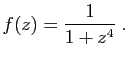
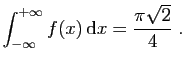
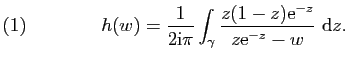
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales