Une application entre deux espaces vectoriels est dite linéaire si elle respecte les deux opérations définissant
la structure.
Une application linéaire 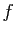 de
de  dans
dans  envoie nécessairement le vecteur nul de
envoie nécessairement le vecteur nul de  sur le vecteur nul de
sur le vecteur nul de
 . Elle envoie l'opposé de
. Elle envoie l'opposé de 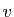 sur l'opposé de
sur l'opposé de 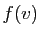 . La
proposition suivante se démontre facilement, dans le style du
théorème 3.
. La
proposition suivante se démontre facilement, dans le style du
théorème 3.
D'une application entre deux ensembles munis d'une structure (groupes,
anneaux, etc.) qui respecte les structures, on dit qu'elle est un
morphisme.
Définition 9
Soient  et
et  deux espaces vectoriels et
deux espaces vectoriels et 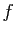 une application de
une application de
 dans
dans  . On dit que l'application
. On dit que l'application
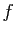 est un :
est un :

- morphisme si elle est linéaire,

- isomorphisme si elle est linéaire et
bijective,

- endomorphisme si elle est linéaire et
 ,
,

- automorphisme si elle est linéaire,
bijective
et
 .
.
Voici quelques exemples d'applications linéaires.

- de
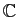 dans
dans
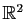 :
:
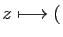 Re
Re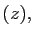 Im
Im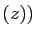

- de
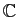 dans
dans
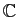 :
:


- de
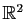 dans
dans
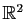 :
:
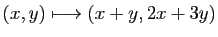

- de
 dans
dans
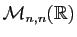 :
:


- de
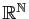 dans
dans
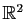 :
:
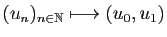

- de
![$ \mathbb{R}[X]$](img178.gif) dans
dans
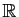 :
:
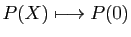

- de
![$ \mathbb{R}[X]$](img178.gif) dans
dans
 :
:
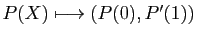

- de
![$ \mathbb{R}[X]$](img178.gif) dans
dans
![$ \mathbb{R}[X]$](img178.gif) :
:
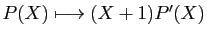

- de l'espace vectoriel des suites convergentes, dans
 :
:
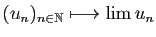

- de l'espace vectoriel des fonctions continûment dérivables,
dans l'espace vectoriel des fonctions continues :
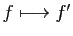

- de l'espace vectoriel des fonctions continues sur
![$ [a,b]$](img291.gif) ,
dans
,
dans
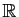 :
:
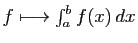
Le fait qu'une application linéaire respecte les combinaisons linéaires
entraîne qu'elle respecte aussi les sous-espaces vectoriels, au
sens suivant.
L'ensemble des images par une application linéaire des éléments
d'un espace vectoriel est un sous-espace vectoriel de l'espace
d'arrivée (point 1). L'ensemble des éléments de l'espace
de départ dont l'image par une application linéaire est dans un
sous-espace de l'espace d'arrivée, est un sous-espace de l'espace de
départ (point 2).
Attention à la notation 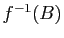 :
elle a un sens même si
l'application
:
elle a un sens même si
l'application 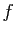 n'est pas bijective et donc même si
l'application réciproque
n'est pas bijective et donc même si
l'application réciproque 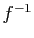 n'existe pas.
Démonstration : Pour montrer qu'un sous-ensemble est un sous-espace vectoriel, il
suffit de vérifier qu'il est non vide, et
que toute combinaison linéaire de deux de ses
vecteurs reste dans l'ensemble (théorème 3).
Rappelons que tout sous-espace vectoriel contient au moins le vecteur
nul, et que si
n'existe pas.
Démonstration : Pour montrer qu'un sous-ensemble est un sous-espace vectoriel, il
suffit de vérifier qu'il est non vide, et
que toute combinaison linéaire de deux de ses
vecteurs reste dans l'ensemble (théorème 3).
Rappelons que tout sous-espace vectoriel contient au moins le vecteur
nul, et que si 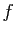 est linéaire alors
est linéaire alors 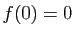 . Donc le vecteur nul
de
. Donc le vecteur nul
de  appartient à
appartient à 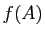 et celui de
et celui de  appartient à
appartient à
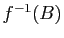 . Les deux ensembles
. Les deux ensembles 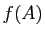 et
et 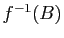 sont donc non
vides.
sont donc non
vides.
- Deux vecteurs quelconques de
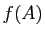 s'écrivent
s'écrivent
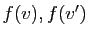 , où
, où
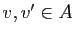 . Etant donnés deux réels
. Etant donnés deux réels 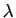 et
et 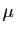 ,
,
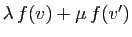 est l'image par
est l'image par 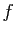 de
de
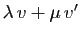 qui est
un vecteur de
qui est
un vecteur de  .
.
- Si
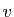 et
et 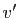 sont tels que
sont tels que 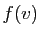 et
et 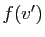 appartiennent à
appartiennent à 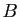 ,
alors
,
alors
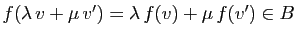 . Donc
. Donc
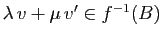 .
.
 Parmi les cas particuliers du théorème 6,
l'image et
le noyau jouent un rôle important.
Parmi les cas particuliers du théorème 6,
l'image et
le noyau jouent un rôle important.
La notation Ker vient de l'allemand, où noyau se dit «Kern».
Proposition 9
Soient  et
et  deux espaces vectoriels et
deux espaces vectoriels et 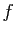 une application
linéaire de
une application
linéaire de  dans
dans  . L'application
. L'application 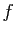 est
est
- surjective si et seulement si
Im
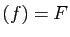
- injective si et seulement si
Ker
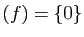
Démonstration : La caractérisation de la surjectivité est une simple traduction
des définitions. Celle de l'injectivité utilise la linéarité.
Soient  et
et 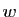 deux éléments de
deux éléments de  .
.
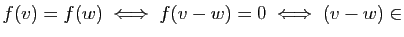
Ker
Par définition,  est injective si et seulement si
est injective si et seulement si
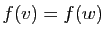 implique
implique 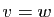 , donc si et seulement si
, donc si et seulement si
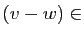 Ker
Ker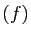 implique
implique 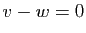 , d'où le résultat.
, d'où le résultat. Considérons la dérivation des polynômes. C'est
l'application
Considérons la dérivation des polynômes. C'est
l'application  de
de
![$ \mathbb{R}[X]$](img178.gif) dans
dans
![$ \mathbb{R}[X]$](img178.gif) qui à un
polynôme associe son polynôme dérivé.
qui à un
polynôme associe son polynôme dérivé.
C'est une application linéaire. L'image de  est
est
![$ \mathbb{R}[X]$](img178.gif) tout
entier (
tout
entier ( est surjective), le noyau de
est surjective), le noyau de 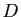 est l'ensemble des
polynômes constants (
est l'ensemble des
polynômes constants (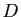 n'est pas injective).
Une telle situation, où l'espace de départ et l'image sont les
mêmes tandis que le noyau est non nul,
est impossible entre espaces vectoriels de
dimension finie.
Reprenons l'exemple de la dérivation des polynômes, mais cette
fois-ci vue comme une application de l'espace
n'est pas injective).
Une telle situation, où l'espace de départ et l'image sont les
mêmes tandis que le noyau est non nul,
est impossible entre espaces vectoriels de
dimension finie.
Reprenons l'exemple de la dérivation des polynômes, mais cette
fois-ci vue comme une application de l'espace
![$ \mathbb{R}_n[X]$](img323.gif) des
polynômes de degré
des
polynômes de degré
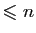 dans
lui-même. L'espace est de dimension
dans
lui-même. L'espace est de dimension 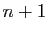 , et la base canonique
est
, et la base canonique
est
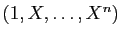 . L'application
. L'application 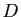 envoie ces
envoie ces
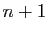 polynômes, respectivement sur
polynômes, respectivement sur
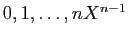 .
Ils engendrent l'espace vectoriel des polynômes de degré
.
Ils engendrent l'espace vectoriel des polynômes de degré
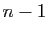 , qui est de dimension
, qui est de dimension 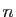 . Le noyau de
. Le noyau de 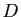 est
est
![$ \mathbb{R}_0[X]$](img329.gif) , et
l'image de
, et
l'image de 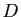 est
est
![$ \mathbb{R}_{n-1}[X]$](img330.gif) .
En dimension finie, la dimension de l'espace de départ est la somme
de la dimension de l'image et de la dimension du noyau : c'est le
théorème du rang.
.
En dimension finie, la dimension de l'espace de départ est la somme
de la dimension de l'image et de la dimension du noyau : c'est le
théorème du rang.
Démonstration : celle que nous donnons ici est
basée sur la notion de supplémentaire.
Soit
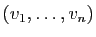 une base de
une base de  . Donc
. Donc
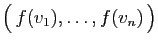 est une famille génératrice
de
Im
est une famille génératrice
de
Im . Donc
Im
. Donc
Im est finiment engendré, et
admet une base. Chacun des éléments de cette base est image d'un
vecteur de
est finiment engendré, et
admet une base. Chacun des éléments de cette base est image d'un
vecteur de  . Notons donc
. Notons donc
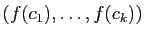 une base
de
Im
une base
de
Im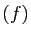 . La famille
. La famille
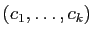 est libre, car sinon
son image par
est libre, car sinon
son image par 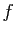 serait liée. Soit
serait liée. Soit  le sous-espace de
le sous-espace de  ,
engendré par
,
engendré par
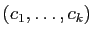 . Nous allons montrer que
. Nous allons montrer que  est un supplémentaire de
Ker
est un supplémentaire de
Ker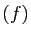 dans
dans  , ce qui implique
le résultat.
Soit
, ce qui implique
le résultat.
Soit 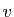 un vecteur quelconque de
un vecteur quelconque de  .
Comme
.
Comme 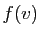 est un vecteur de
Im
est un vecteur de
Im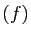 , il s'écrit :
, il s'écrit :
Posons :
Alors :
Donc
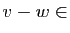 Ker
Ker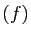 . Donc
. Donc 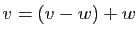 est somme d'un vecteur de
Ker
est somme d'un vecteur de
Ker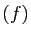 et d'un vecteur de
et d'un vecteur de  . Pour montrer que la somme est
directe, nous devons montrer que l'intersection est réduite au
vecteur nul. Prenons un vecteur de
. Pour montrer que la somme est
directe, nous devons montrer que l'intersection est réduite au
vecteur nul. Prenons un vecteur de  sous la forme :
sous la forme :
S'il appartient aussi à
Ker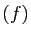 , son image est nulle :
, son image est nulle :
Mais puisque
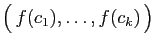 est une famille
libre, ceci entraîne que les
est une famille
libre, ceci entraîne que les 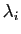 sont tous nuls, donc
sont tous nuls, donc 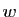 est le vecteur nul.
est le vecteur nul. 
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
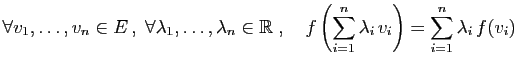
![]() :
elle a un sens même si
l'application
:
elle a un sens même si
l'application ![]() n'est pas bijective et donc même si
l'application réciproque
n'est pas bijective et donc même si
l'application réciproque ![]() n'existe pas.
Démonstration : Pour montrer qu'un sous-ensemble est un sous-espace vectoriel, il
suffit de vérifier qu'il est non vide, et
que toute combinaison linéaire de deux de ses
vecteurs reste dans l'ensemble (théorème 3).
Rappelons que tout sous-espace vectoriel contient au moins le vecteur
nul, et que si
n'existe pas.
Démonstration : Pour montrer qu'un sous-ensemble est un sous-espace vectoriel, il
suffit de vérifier qu'il est non vide, et
que toute combinaison linéaire de deux de ses
vecteurs reste dans l'ensemble (théorème 3).
Rappelons que tout sous-espace vectoriel contient au moins le vecteur
nul, et que si ![]() est linéaire alors
est linéaire alors ![]() . Donc le vecteur nul
de
. Donc le vecteur nul
de ![]() appartient à
appartient à ![]() et celui de
et celui de ![]() appartient à
appartient à
![]() . Les deux ensembles
. Les deux ensembles ![]() et
et ![]() sont donc non
vides.
sont donc non
vides.
![\begin{displaymath}
\begin{array}{rcl}
&D&\\
\mathbb{R}[X]&\longrightarrow&\mat...
...)&
\longmapsto& P'(X)=a_1+2a_2X+\cdots+na_nX^{n-1}.
\end{array}\end{displaymath}](img322.gif)
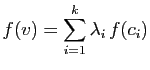
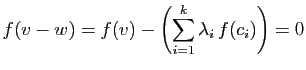
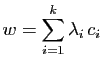
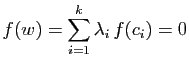
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales