La théorie de la dimension, qui est
traitée dans un autre chapitre, est supposée connue. Nous
rappelons ici quelques uns des principaux résultats.
Définition 7
Soit  un espace vectoriel contenant des vecteurs non nuls.
On dit que
un espace vectoriel contenant des vecteurs non nuls.
On dit que  est finiment
engendré s'il est engendré par une famille finie de vecteurs.
Soit
est finiment
engendré s'il est engendré par une famille finie de vecteurs.
Soit
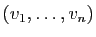 un
un 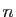 -uplet de vecteurs de
-uplet de vecteurs de  . On dit que
. On dit que
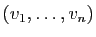 est une base de
est une base de  si c'est à la fois une
famille génératrice et libre.
si c'est à la fois une
famille génératrice et libre.
Le résultat le plus important est le théorème suivant.
Théorème 4
Dans un espace vectoriel contenant des vecteurs non nuls,
finiment engendré, il existe des bases et
toutes les bases ont le même nombre d'éléments.
Ceci permet d'appeler dimension de l'espace, le cardinal commun
de toutes les bases. On convient de dire que l'espace contenant
uniquement le vecteur nul, est de dimension 0.
Les coordonnées d'un vecteur sont définies grâce au
résultat suivant.
Les réels
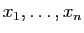 sont les
coordonnées de
sont les
coordonnées de 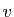 dans la base
dans la base
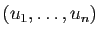 .
Considérons par exemple l'espace vectoriel des polynômes de
degrés inférieurs ou égaux à 3. C'est un espace vectoriel de
dimension 4, dont la base la plus naturelle (base canonique) est :
.
Considérons par exemple l'espace vectoriel des polynômes de
degrés inférieurs ou égaux à 3. C'est un espace vectoriel de
dimension 4, dont la base la plus naturelle (base canonique) est :
Dans cette base, les coordonnées du polynôme 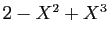 sont
sont
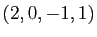 . Considérons maintenant une nouvelle famille.
. Considérons maintenant une nouvelle famille.
C'est une famille de polynômes de degrés distincts, donc par la
proposition 5, c'est une famille libre. Dans un espace
de dimension 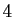 , une famille libre de
, une famille libre de 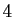 éléments est
forcément génératrice : c'est une base. Le polynôme
éléments est
forcément génératrice : c'est une base. Le polynôme
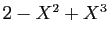 s'écrit de façon unique comme combinaison
linéaire des éléments de
cette nouvelle base :
s'écrit de façon unique comme combinaison
linéaire des éléments de
cette nouvelle base :
Les coordonnées de 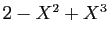 dans la nouvelle base sont donc
dans la nouvelle base sont donc
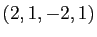 .
Dans un espace vectoriel de dimension finie, tout sous-espace est
lui-même de dimension finie, inférieure ou égale à celle de
l'espace.
Le théorème de la base incomplète dit que dans un espace
vectoriel de dimension finie, toute famille libre peut être
complétée en une base de l'espace. On en déduit immédiatement
l'existence de supplémentaires.
.
Dans un espace vectoriel de dimension finie, tout sous-espace est
lui-même de dimension finie, inférieure ou égale à celle de
l'espace.
Le théorème de la base incomplète dit que dans un espace
vectoriel de dimension finie, toute famille libre peut être
complétée en une base de l'espace. On en déduit immédiatement
l'existence de supplémentaires.
Démonstration : Soit
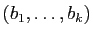 une base de
une base de  . Le théorème de la base
incomplète affirme qu'il existe des vecteurs
. Le théorème de la base
incomplète affirme qu'il existe des vecteurs
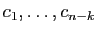 tels que :
tels que :
soit une base de  . Soit
. Soit  l'espace engendré par
l'espace engendré par
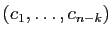 . Tout vecteur de
. Tout vecteur de  s'écrit :
s'écrit :
La première somme est un vecteur de  , la seconde un vecteur de
, la seconde un vecteur de
 , donc
, donc 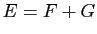 . Il reste à vérifier que l'intersection est
réduite au seul vecteur nul. Si
. Il reste à vérifier que l'intersection est
réduite au seul vecteur nul. Si
alors nécessairement tous les coefficients 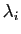 et
et 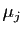 sont nuls, car
sont nuls, car
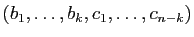 est une famille
libre. D'où le résultat.
est une famille
libre. D'où le résultat. La proposition suivante relie la dimension d'une somme de sous-espaces
vectoriels à celles des composants.
La proposition suivante relie la dimension d'une somme de sous-espaces
vectoriels à celles des composants.
Proposition 7
Soit  un espace vectoriel,
un espace vectoriel,  et
et  deux sous-espaces vectoriels,
de dimensions finies.
deux sous-espaces vectoriels,
de dimensions finies.
Démonstration : Choisissons un supplémentaire 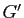 de
de 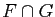 dans
dans  . La
somme de
. La
somme de  et
et 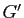 est directe, car
est directe, car
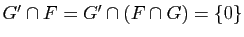 . Donc :
. Donc :
Or
dim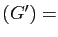 dim
dim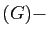 dim
dim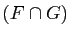 . Donc :
. Donc :

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
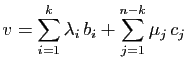
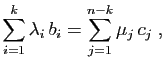
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales